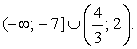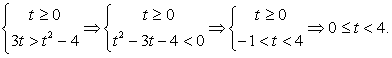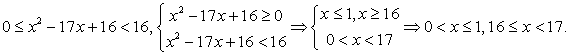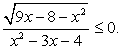Комментарий. Цель этого раздела — предоставить абитуриентам теоретические сведения и практический материал для формирования навыков решения алгебраических уравнений и неравенств. Алгебраические уравнения и неравенства играют важную роль, т.к. в большинстве случаев именно к ним приводят как простые тригонометрические, логарифмические, показательные уравнения и неравенства, так и комбинированные задания. Решение большинства текстовых задач (сюжетных) — задач на движение, на работу, на смеси и сплавы — также сводится к решению алгебраического уравнения или системы алгебраических уравнений.
В рамках данного раздела целесообразно выделить следующие вопросы.
-
Решение рациональных уравнений.
-
Решение рациональных неравенств.
-
Рациональные уравнения и неравенства с модулями.
-
Решение дробно-рациональных неравенств.
-
Иррациональные уравнения и неравенства.
Часто трудности с решением рациональных уравнений обусловлены для абитуриентов тем, что решение, как говорится «в лоб», по алгоритму метода разложения на множители:
обусловлены для абитуриентов тем, что решение, как говорится «в лоб», по алгоритму метода разложения на множители:
где A (x), B (x) — произвольные рациональные выражения;
P (x), Q (x) — многочлены,
приводит к громоздким, «рутинным» преобразованиям или к необходимости находить корни многочленов степени большей, чем второй. А это уже не совсем «школьная» задача. При этом даже в самых очевидных случаях, абитуриенты не применяют метод введения новой переменной. А ведь, введение новой переменной позволяет быстро упростить решаемое уравнение. Это мощный метод, его следует понимать и применять.
Введение новой переменной осуществляется тогда, когда решаемое уравнение представимо в виде f (g (x)) = 0. Полагая g (x) = t, мы переходим к решению системы:
Если уравнения f (t) = 0, g(x) = t1 , g(x) = t2 ,…, g (x) = tn , где t1 , t2 ,…, tn — корни уравнения f (t) = 0 проще исходного уравнения, то метод, как говорится, сработал.
Рассмотрим различные рациональные уравнения, для решения которых весьма полезен метод введения новой переменной, но не очевидны случаи, когда исходное уравнение непосредственно имеет вид f (g(x)) = 0. Поиск удачной подстановки g (x) = t и специальная работа по приведению исходного уравнения к указанному виду, составляет главную сущностную часть решения уравнения. Решение же уравнения f (t) = 0 и совокупности уравнений g (x) = ti — сравнительно несложная, техническая часть процесса решения уравнения.
Решение дробно-рациональных уравнений нередко сводится к решению обычных квадратных уравнений, но с учетом ограничений на допустимые значения неизвестного. В частности, из ОДЗ исключаются те значения х, при которых хотя бы один из знаменателей дробей, входящих в уравнение, обращается в 0.
Этапы решения рационального уравнения.
-
Определить ОДЗ (ни один знаменатель не может равняться нулю).
-
Найти наименьший общий знаменатель всех дробей.
-
Умножить уравнение на этот знаменатель и решить полученное целое уравнение.
-
Включить в ответ только те корни, которые входят в ОДЗ.
Для решения рациональных неравенств применяют так называемый метод интервалов. Практика вступительных испытаний по математике показывает, что абитуриенты не всегда правильно используют этот метод, понимают его сущность и специфику. В значительной степени это связано с тем, что в учебной литературе встречаются различные подходы к изложению метода интервалов, далеко не всегда удачные. Имеет место путаница с терминами, «странные синтезы», сразу нескольких подходов. Но алгоритм метода интервал требует строгости и четкости.
применяют так называемый метод интервалов. Практика вступительных испытаний по математике показывает, что абитуриенты не всегда правильно используют этот метод, понимают его сущность и специфику. В значительной степени это связано с тем, что в учебной литературе встречаются различные подходы к изложению метода интервалов, далеко не всегда удачные. Имеет место путаница с терминами, «странные синтезы», сразу нескольких подходов. Но алгоритм метода интервал требует строгости и четкости.
Будем понимать метод интервалов, как метод, применяемых для решения рациональных неравенств строго определенного вида:
где x1 , x2 , x3 , …, xn ϵ R; α1 , α2 , α3 ,…, αn ϵ N и V — любой из знаков неравенства >, <, ≥, ≤.
Если данное неравенства не соответствует указанному виду, то его необходимо привести к этому виду теми или иными равносильными преобразованиями, и лишь затем применять метод интервалов. Назовем указанный вид неравенства стандартным для решения методом интервалов.
для решения методом интервалов.
Введем еще два термина. Пусть 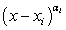 — множитель, входящий в неравенство, стандартное для решения методом интервалов. Если показатель степени αi
— нечетное число, то точку х = xi
будем называть простой. Если показатель степени αi
— четное число, то точку х = xi
будем называть двойной.
— множитель, входящий в неравенство, стандартное для решения методом интервалов. Если показатель степени αi
— нечетное число, то точку х = xi
будем называть простой. Если показатель степени αi
— четное число, то точку х = xi
будем называть двойной.
Теперь сформулируем алгоритм метода интервалов .
.
Пусть дано неравенство вида, стандартного для решения методом интервалов. Для его решения:
1) отметим на числовой прямой точки, соответствующие числам x1 , x2 , x3 ,…, xn , разбив тем самым всю числовую прямую на промежутки (интервалы); причем, если знак неравенства строгий, то точки отмечаются выколотыми, если знак неравенства нестрогий, то точки отмечаются сплошными;
2) на каждом из полученных промежутков выражение 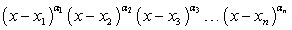 будем сохранять свой знак постоянным; расставим эти знаки пользуясь правилом чередования знаков:
будем сохранять свой знак постоянным; расставим эти знаки пользуясь правилом чередования знаков:
а) в крайнем правом интервале всегда знак «плюс»;
б) при переходе через простую точку знак меняется, на противоположный;
в) при переходе через двойную точку знак сохраняется;
3) после того как знаки всех промежутков определены с полученного рисунка, считывается решение неравенства; ответ записывается в виде объединения промежутков.
Метод интервалов можно применять и для решения дробных рациональных неравенств, если воспользоваться равносильностями:
Основной метод решения рациональных (и многих других) неравенств — метод интервалов. Для его применения нужно преобразовать неравенство так, чтобы в правой его части стоял 0, а левая была произведением нескольких множителей или дробью, числитель и знаменатель которой разложены на множители. Затем находятся корни каждого множителя (то есть от решения неравенства вы переходите к решению уравнений), и среди них выделяются такие, в которых ни один из имеющихся множителей не меняет знак, или меняет знак четное количество множителей. В дальнейшем такие корни, если они найдутся, мы будем называть кратными (хотя это не совсем точно). Для окончательного решения неравенства остается нанести найденные корни на числовую прямую, найти знак левой части неравенства только на одном интервале, ограниченном полученными точками, и расставить знаки на остальных интервалах, меняя их при переходе через простой корень и не меняя при переходе через кратный.
Рациональные уравнения и неравенства
и неравенства в работах ЕГЭ часто «усложнены модулями». Уравнения и неравенства, содержащие переменную под знаком модуля, не входят явно в школьную программу по математике, часто предлагаются школьными учителями как задания повышенной сложности. В итоге, вызывая у абитуриентов страх и трепет, такие задания многими абитуриентами просто пропускаются, хотя вполне могли быть выполнены. Для этого необходимо не так много:
в работах ЕГЭ часто «усложнены модулями». Уравнения и неравенства, содержащие переменную под знаком модуля, не входят явно в школьную программу по математике, часто предлагаются школьными учителями как задания повышенной сложности. В итоге, вызывая у абитуриентов страх и трепет, такие задания многими абитуриентами просто пропускаются, хотя вполне могли быть выполнены. Для этого необходимо не так много:
1) четко знать определение модуля;
2) понимать суть приема решения уравнений и неравенств, основанного на одновременном раскрытии всех модулей (причем, здесь достаточно конкретных примеров);
3) помнить о методе введения новой переменной.
Решение уравнений и неравенств, содержащих переменную под знаком модуля, основано на определении модуля:
Модули, входящие в уравнение или неравенство раскрываются по определению и в дальнейшем уже решаются уравнения и неравенства, не содержащие модуля. Заметим, что абитуриенты часто вместо равенства, указанного выше, применяют равенство:
Понятно, что оно справедливо лишь в случае f(x) = x. В общем случае это равенство неверно. Следует помнить об этом и не допускать этой распространенной среди абитуриентов ошибки.
Решение дробно-рациональных уравнений нередко сводится к решению обычных квадратных уравнений, но с учетом ограничений на допустимые значения неизвестного. В частности, из ОДЗ исключаются те значения х, при которых хотя бы один из знаменателей дробей, входящих в уравнение, обращается в 0.
Основной прием решения модульных уравнений и неравенств — раскрытие модуля с использованием его определения (| a | = a при a ≥ 0 и | a | = -a при a < 0). Для этого обычно рассматривают отдельно два случая: случай, когда подмодульное выражение неотрицательно и когда оно отрицательно.
Хочется сразу предостеречь вас от самой распространенной ошибки: умножения обеих частей неравенства на общий знаменатель. Если при разных значениях х знаменатель может менять знак, то избавляться от него нельзя. Почему? Потому что при умножении обеих частей неравенства на положительное число знак неравенства не меняется, а на отрицательное — меняется на обратный. Поэтому, решая такое неравенство, вы должны учитывать знак не только числителя, но и знаменателя. Этапы решения дробно-рациональных неравенств можно описать так:
можно описать так:
1) перенести все слагаемые в левую часть неравенства;
2) привести левую часть к наименьшему общему знаменателю;
3) найти корни числителя и знаменателя полученной дроби; проверить, есть ли среди них кратные;
4) решить неравенство методом интервалов с учетом кратных корней.
Весьма распространенный прием решения иррациональных уравнений и неравенств
и неравенств — возведение в квадрат. Тем не менее, советуем вам пользоваться им как можно реже, ибо он обладает существенными недостатками: во-первых, возводя в квадрат обе части уравнения, вы расширяете область допустимых значений неизвестного, что может привести к появлению посторонних корней; во-вторых, часто в результате этой операции получается уравнение с громоздкими коэффициентами, работать с которыми затруднительно (особенно если на экзамене не разрешается пользоваться калькулятором). Наконец, главный недостаток этого приема — увеличение вдвое степени уравнения. Возведя обе части в квадрат, вы можете избавиться от иррациональностей, но получить рациональное уравнение степени выше второй, способы решения которого в общем виде вам неизвестны или вообще не существуют.
— возведение в квадрат. Тем не менее, советуем вам пользоваться им как можно реже, ибо он обладает существенными недостатками: во-первых, возводя в квадрат обе части уравнения, вы расширяете область допустимых значений неизвестного, что может привести к появлению посторонних корней; во-вторых, часто в результате этой операции получается уравнение с громоздкими коэффициентами, работать с которыми затруднительно (особенно если на экзамене не разрешается пользоваться калькулятором). Наконец, главный недостаток этого приема — увеличение вдвое степени уравнения. Возведя обе части в квадрат, вы можете избавиться от иррациональностей, но получить рациональное уравнение степени выше второй, способы решения которого в общем виде вам неизвестны или вообще не существуют.
Если возводить в квадрат все-таки приходится, нужно внимательно следить за тем, чтобы не включить в ответ посторонние корни. В частности, если уравнение имеет вид 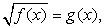 то для корней должно выполняться условие
то для корней должно выполняться условие 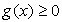 (при этом
(при этом 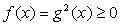 , и условие
, и условие 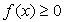 отдельно ставить не требуется). Еще один способ обнаружить посторонние корни — проверка всех найденных корней подстановкой их в первоначальное уравнение.
отдельно ставить не требуется). Еще один способ обнаружить посторонние корни — проверка всех найденных корней подстановкой их в первоначальное уравнение.
Пример 5.1.
Решение
Раскрыв скобки в знаменателях, получаем уравнение:
Полагая, что x2 + 3х + 2 = t приходим к системе уравнений:
Решив первое уравнение системы, получаем корни t1
= 2, t2
= 18. Далее, из второго уравнения системы, получаем корни исходного уравнения: 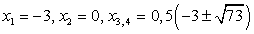 .
.
Пример 5.2.
Решение
Прибавим к числителю второй дроби выражение 2х - 2х, тождественно равное нулю:
Полагая 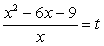 , приходим к системе уравнений:
, приходим к системе уравнений:
Решив первое уравнение системы, получаем корни: t1 = -1, t2 = 2. Из второго уравнения системы, получаем корни исходного уравнения:
Пример 5.3.
Решение
Полагая, что 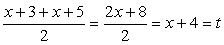 , приходим к системе уравнений:
, приходим к системе уравнений:
Решим первое уравнение системы, воспользовавшись формулой:
Имеем:
Решив полученное биквадратное уравнение, получаем корни t1, 2 = ± 1 и соответственно: x1 = -5, x2 = -3.
Ответ: -5; -3.
Пример 5.4.
Решение
Принимая во внимание тождество 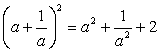 , перепишем данное уравнение в виде:
, перепишем данное уравнение в виде:
Полагая, что 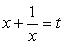 , имеем систему уравнений:
, имеем систему уравнений:
4t2 + 12t - 55 = 0,
Решив первое уравнение системы, получаем корни: 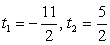 .
.
Из второго уравнения системы получаем корни исходного уравнения: 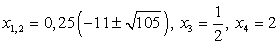 .
.
Пример 5.5.
Решение
Левая часть уравнения представляет собой сумму квадратов. Для решения уравнения, удобно превратить ее в полный квадрат, добавив к обеим частям уравнения соответствующее удвоенное произведение:
Полагая, что 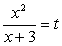 , имеем систему уравнений:
, имеем систему уравнений:
Решив первое уравнение системы, получаем корни t1 = -9, t2 = 3. Далее, из второго уравнения системы, получаем корни исходного уравнения:
Пример 5.6.
Решение
Положим, что x2 + х + 4 = t. Тогда заданное уравнение принимает вид:
t2 + 8xt + 15x2 = 0.
Решив это уравнение как квадратное относительно t, получаем:
Совокупность уравнений:
дает корни исходного уравнения: 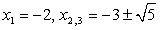
Комментарий. Метод введения новой переменной иногда называют методом замены переменной . Это не совсем правомерно. Введение новой переменной в уравнение отнюдь не предполагает обязательное исчезновение из уравнения старой переменной.
. Это не совсем правомерно. Введение новой переменной в уравнение отнюдь не предполагает обязательное исчезновение из уравнения старой переменной.
Пример 5.7.
Решение
Пусть x0 — корень уравнения. Введем новые неизвестные u = 2 - x0 и х = x0 - 3. Понятно, что термин «новые переменные» в данном случае был бы применен неправильно. U и v — хотя и неизвестные, но постоянные величины, ибо х0 — постоянная, а отнюдь не переменная величина.
Имеем систему уравнений:
Воспользовавшись формулой:
имеем:
Учитывая, что u + v = -1, из второго уравнения системы получаем:
Таким образом, либо uv = 1, либо uv = 0 и для нахождения u и v имеем две системы уравнений (совокупность систем):
Первая система решений не имеет.
Корни второй системы: u1 = 0, v1 = -1 и u2 = -1, v2 = 0. Отсюда либо x0 = 2, либо x0 = 3.
Итак, корни исходного уравнения: x1 = 2, x2 = 3.
Ответ: 2; 3.
Комментарий. Особый случай применения метода введения новой переменной связан с решением уравнения с двумя переменными: новой и старой. Другой особый случай использования метода введения новой переменной — введение нескольких новых неизвестных. В этом случае решение исходного уравнения сводится к решению системы уравнений относительно новых неизвестных.
Пример 5.8.
Решение
Приведем данное неравенство к виду стандартному для решения методом интервалов:
Построим разбиение числовой прямой на промежутки:
Заметим, что масштаб в данном случае соблюдать совсем необязательно, но отдельные принципиальные детали, относящиеся к уровню общей графической культуры, соблюдать конечно следует. Так, точка -3 должна быть изображена более удаленной от нуля, чем точка 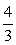 , а расстояние между точками
, а расстояние между точками 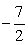 и -3 должно быть значительно меньше, чем расстояние между точками
и -3 должно быть значительно меньше, чем расстояние между точками 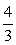 и 6 и т.д.) Расставим знаки в промежутках, используя правило чередования:
и 6 и т.д.) Расставим знаки в промежутках, используя правило чередования:
Из рисунка видно решение неравенства: 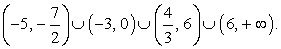
Пример 5.9.
Решение
Раскроем скобки; имеем:
Так как x2
+ х + 1 > 0 при всех х и x2
+ 1 > 0 при всех х, то получаем неравенство вида, стандартного для решения методом интервалов и равносильное исходному неравенству: 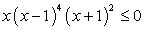
Построим разбиение числовой прямой на промежутки и расставим знаки по правилу чередования:
Таким образом, решение неравенства: 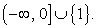
Пример 5.10.
Решение
Данное неравенство равносильно системе:
Приведем первое неравенство системы к виду, стандартному для решения методом интервалов:
Построим разбиение числовой прямой на промежутки, учитывая второе неравенство системы, то есть, что х ≠ 3, х ≠ 7, х ≠ ± 4, и расставим знаки по правилу чередования:
Комментарий. На материал, следующий ниже, советуем обратить особое внимание, поскольку в школе ему редко уделяют должное внимание.
Значительно содействуют пониманию сущности метода интервалов, а значит и лучшему его применению упражнения на конструирование неравенств по заданным объединениям промежутков — их решениям. Рассмотрим пример.
Пример 5.11.
Составим неравенство, решение которого (-∞, -10) U [-7, -4] U (-4, 2) U {6} U [11, +∞].
Решение
Прежде всего, отметим все необходимые точки на числовой прямой:
Теперь произвольно выберем знак составляемого неравенства (ясно, что этот знак нестрогого неравенства, поскольку на нашем рисунке есть сплошные точки) и в соответствии с данным решением неравенства расставим знаки. Итак, пусть знак нашего неравенства ≥, тогда имеем:
Из рисунка видно, что точки х = -10, х = -7, х = 2 и х = 11 — простые точки, а точки х = -4, х = 6 — двойные точки. Кроме того, поскольку на рисунке есть и выколотые и сплошные точки, то составляемое неравенство — дробное рациональное. Учитывая все эти выводы, получаем, например:
или, если перемножить скобки:
Комментарий. Напомним, что несколько неравенств образуют систему, если поставлена задача отыскания всех тех значений переменной, при которых справедливо каждое из рассматриваемых неравенств. Для решения системы неравенств, таким образом, необходимо решить каждое из неравенств системы, а затем найти пересечение этих решений.
Пример 5.12.
Решение
Решим каждое из неравенств системы.
Решение первого неравенства:
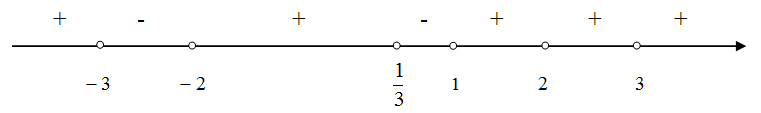
Решение второго неравенства:
Теперь найдем пересечение решений неравенств. Для этого на одной числовой прямой изобразим оба решения, отмечая их штриховкой разного наклона. Искомым пересечением решений, ясно, будут промежутки двойной штриховки:
Пример 5.13.
Решение
Понятно, что речь идет о решении системы неравенств:
Решим каждое из неравенств системы.
Решение первого неравенства:
Решение второго неравенства:
x ϵ (-8, -5) U (0,5).
Найдем пересечение решений неравенств:
Таким образом, решение системы, то есть решение данного двойного неравенства: 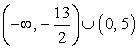
Пример 5.14.
Решение
Раскроем все входящие в уравнение модули. Для этого на числовой прямой отметим сплошными точками корни всех подмодульных выражений. Числовая прямая тем самым будет разбита на несколько промежутков. На каждом из промежутков укажем знак каждого из подмодульных выражений.
Таким образом, надо рассмотреть четыре различных случая:
Решение второй и четвертой систем пустое множество. Таким образом, корни данного уравнения: 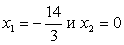
Пример 5.15.
Решение
Раскроем модули, поступив так же как в примере 5.14.
Рассмотрим четыре случая:
Решение уравнения свелось к решению совокупности четырех смешанных систем. В итоге получаем:
Первая и четвертая системы несовместны, решение второй системы также пустое множество.
Это и есть единственный корень данного уравнения.
Пример 5.16.
Решение
Раскроем модули.
Таким образом, имеем:
Решение неравенства свелось к решению совокупности систем неравенств:
Следовательно, решение данного неравенства:
Пример 5.17.
Решение
Запишем уравнение несколько иначе:
Поскольку 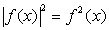 , то имеем уравнение
, то имеем уравнение 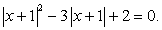
Положим 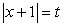 , тогда t2
- 3t + 2 = 0. Так как t1
= 1 и t2
= 2, то имеем совокупность уравнений:
, тогда t2
- 3t + 2 = 0. Так как t1
= 1 и t2
= 2, то имеем совокупность уравнений:
Очевидно, что х = 0 и х = -2 (это корни первого уравнения совокупности); х = 1 и х = -3 (это корни второго уравнения совокупности). Таким образом, корни данного уравнения: x1 = -3, x2 = -2, x3 = 0 и x4 = 1.
Ответ: x1 = -3, x2 = -2, x3 = 0 и x4 = 1.
Пример 5.18.
Решение
Пусть 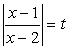 , тогда t2
+ t – 12 < 0, имеем (t + 4 )(t - 3) < 0.
, тогда t2
+ t – 12 < 0, имеем (t + 4 )(t - 3) < 0.
Решение последнего неравенства — интервал (-4, 3). Таким образом, решение данного неравенства сводится к решению двойного неравенства: 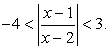
Поскольку 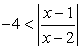 при всех допустимых значениях х, то осталось решить лишь неравенство
при всех допустимых значениях х, то осталось решить лишь неравенство 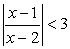 Отметим на числовой прямой х = 1 — точку, зануляющую подмодульное выражение и х = 2 — точку, в которой подмодульное выражение не существует. Расставим знаки подмодульного выражения в каждом из трех полученных промежутков.
Отметим на числовой прямой х = 1 — точку, зануляющую подмодульное выражение и х = 2 — точку, в которой подмодульное выражение не существует. Расставим знаки подмодульного выражения в каждом из трех полученных промежутков.
Таким образом, мы имеем два случая:
Решение неравенства сводится, таким образом, к решению совокупности систем:
Таким образом, решение данного неравенства: 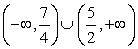 .
.
Пример 5.19.
Решение
Найдем наименьший общий знаменатель трех дробей (важно привести их не просто к общему знаменателю, а именно к наименьшему, иначе в результате может получиться уравнение слишком высокой степени, решить которое мы не сумеем).
Разложим на множители второй и третий знаменатели:
Тогда наименьший общий знаменатель имеет вид:
(х - 4)(х + 4)(x2 - 4х + 16).
Теперь можно умножить обе части уравнения на найденный общий знаменатель. Равенство при этом не нарушится, так как при условии, что x ≠ ±4, то есть в рамках ОДЗ, общий знаменатель не равен 0.
После этого нужно решить уравнение:
После упрощения получаем:
x2 + 12х + 32 = 0.
Корни этого уравнения: x1 = -8 и x2 = -4, но число -4 не входит в ОДЗ. С учетом этого оказывается, что уравнение имеет единственное решение: х = 8.
Ответ: х = 8.
Пример 5.20.
Решение
Применим ту же последовательность действий.
Для определения ОДЗ найдем корни всех знаменателей:
x2 - 14х + 24 = 0; x1 = 2, x2 = 12.
x2 - 16х + 48 = 0; x1 = 4, x2 = 12.
х - 4 = 0; х = 4.
Следовательно, ОДЗ имеет вид: х ≠ 2, х ≠ 4, х ≠ 12.
x2 - 14х + 24 = (х - 2)(х - 12), x2 - 16х + 48 = (х - 4)(х - 12), наименьший общий знаменатель равен (х — 2)(х — 4)(х — 12). Умножим на него обе части равенства:
5(х - 4) - 4(х - 2) = x2 - 14х + 24; x2 - 15х + 36 = 0; x1 = 3, x2 = 12 — посторонний корень (не входит в ОДЗ).
Ответ: х = 3.
Пример 5.21.
Решение
Если записать уравнение в виде 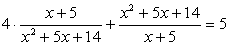 , то можно заметить, что его левая часть содержит две взаимно обратные дроби. Введем новое неизвестное:
, то можно заметить, что его левая часть содержит две взаимно обратные дроби. Введем новое неизвестное: 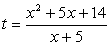 , тогда
, тогда 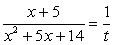 , и уравнение для t выглядит так:
, и уравнение для t выглядит так: 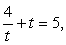 или t2
- 5t + 4 = 0.
или t2
- 5t + 4 = 0.
Отсюда: t1 = 1, t2 = 4.
Ответ: x = 2, x = -3.
Комментарий. Обратите внимание на то, что попытка решить это уравнение приведением к общему знаменателю привела бы нас к уравнению четвертой степени, общая формула корней которого вам не известна. С помощью замены уравнение преобразовано в квадратное, техника решения которого проста.
Пример 5.22.
Решение
Раскроем скобки в знаменателях левой части уравнения: 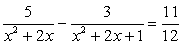 .
.
Видим, что х дважды входит в выражение x2 + 2х и больше в уравнении не присутствует.
Сделаем замену: t = x2
+ 2x и решим уравнение 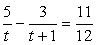 .
.
Упрощая, получим: 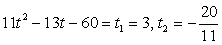 (оба значения входят в ОДЗ).
(оба значения входят в ОДЗ).
Ответ: х = 1, х = -3.
Пример 5.23.
Решение
ОДЗ: х ≠ 0, х ≠ 3.
Обратим внимание на то, что дробь, стоящая во втором слагаемом, равна произведению дробей, возводимых в квадрат в первом и третьем слагаемых, и введем две новые неизвестные: 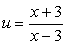 и
и 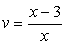 . Они должны удовлетворять уравнению u2
- 7uv + 6v2
= 0. Это однородное уравнение второй степени. Поскольку v ≠ 0 (так как х ≠ 3), можно разделить обе части равенства на v2
:
. Они должны удовлетворять уравнению u2
- 7uv + 6v2
= 0. Это однородное уравнение второй степени. Поскольку v ≠ 0 (так как х ≠ 3), можно разделить обе части равенства на v2
: 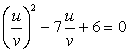 . Пусть
. Пусть 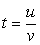 , тогда:
, тогда:
t2 - 7t + 6 = 0, t1 = 1, t2 = 6.
Ответ: х = 1, х = 1,8, х = 6.
Комментарий. Замена переменной — очень удобный способ решения уравнений (и не только рациональных). Конечно, подходящую замену нужно «увидеть», а для этого необходимо накапливать опыт — только он поможет вам быстро найти наиболее удачный вид нового неизвестного.
Отдельный вид уравнений, которые можно с помощью замены свести к квадратному, — так называемые возвратные уравнения , а именно уравнения вида:
, а именно уравнения вида:
ax4 + bx3 + cx2 + dx + f = 0,
где числа a, b, d и f не равны нулю и выполняется равенство: 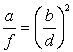 .
.
Пример 5.24.
6x4 - 13x3 - 57x2 - 39х + 54 = 0.
Решение
Убедимся, что перед нами возвратное уравнение: 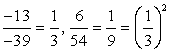 .
.
Так как х = 0 не является решением уравнения, разделим обе его части на x2 :
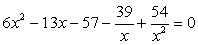 и перегруппируем слагаемые так:
и перегруппируем слагаемые так:
Тогда 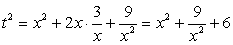 , следовательно,
, следовательно, 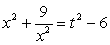 , и для t получаем уравнение:
, и для t получаем уравнение:
6(t2 - 6) - 13t - 57 = 0, или
Пример 5.25.
x3 + 4x2 - х - 4 = 0.
Решение
Преобразуем левую часть уравнения:
x3 + 4x2 - х - 4 = x2 (х + 4) - (х + 4) = (x2 - 1)(х + 4). Тем самым уравнение приведено к виду (x2 — 1)(х + 4) = 0, откуда x1 = 1, x2 = - 1, x3 = - 4.
Ответ: х = 1, х = -1, х = -4.
Комментарий. Если группировка не получается, можно попытаться найти хотя бы один корень подбором, а затем разделить левую часть уравнения на разность х - x0 , где x0 — найденный корень. Напомним, что в уравнении с целыми коэффициентами все целочисленные корни являются делителями свободного члена.
Пример 5.26.
x3 + 8x2 + 19х + 12 = 0.
Решение
Выпишем все делители числа 12: ±1, ±2, ±3, ±4, ±6, ±12. Очевидно, что уравнение не может иметь положительных корней, так как при подстановке вместо х любого положительного числа левая часть примет положительное значение. Поэтому начнем поиск корней с числа -1 и убедимся, что оно при подстановке в уравнение обращает его в верное равенство. Итак, x1 = -1 — корень, найденный подбором. Разделим «уголком» левую часть уравнения на х - 1:
(x3 + 8x2 + 19х + 12 ) : (х - 1) = (x2 + 7х + 12).
Следовательно, уравнение можно записать в виде:
(х - 1)(x2 + 7х + 12) = 0, откуда x2 = -3, x3 = -4.
Ответ: х = - 1, х = - 3, х = - 4.
Пример 5.27.
Решение
Перенесем все слагаемые в левую часть и разложим ее на множители, используя формулу разности квадратов:
(х - 6 + х - 4)(х - 6 - х + 4) > 0, (2x - 10)(-2) > 0.
Левая часть неравенства равна 0 при х = 5 и меняет знак в этой точке. При х = 0 (-10)(-2) > 0, поэтому знаки на координатной прямой распределяются следующим образом:
Следовательно, решением неравенства является интервал (- ∞; 5).
Ответ: (- ∞; 5).
Пример 5.28.
Решить неравенство: (x2 - 6х + 8)(x2 - 11х + 28) < 0.
Решение
После разложения на множители получаем: (х - 2)(х - 4)2 (х - 7) < 0.
х = 4 — кратный корень, потому что (x - 4)2
> 0 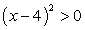 и при x < 4, и при x > 4. Поэтому на интервалах, разделенных точкой 4, левая часть неравенства будет иметь одинаковые знаки, а точки 2 и 7 разделяют интервалы с разными знаками левой части. При х = 0 левая часть неравенства положительна, следовательно, знаки распределяются так:
и при x < 4, и при x > 4. Поэтому на интервалах, разделенных точкой 4, левая часть неравенства будет иметь одинаковые знаки, а точки 2 и 7 разделяют интервалы с разными знаками левой части. При х = 0 левая часть неравенства положительна, следовательно, знаки распределяются так:
Ответ: (2; 4) U (4; 7).
Пример 5.29.
Решение
Перенесем все слагаемые в правую часть и прочтем неравенство «справа налево»:
Теперь заметим, что в левой части полученного неравенства стоит полный квадрат:
Значит, неравенство будет верным при любом значении х, кроме тех, при которых его левая часть равна нулю, то есть кроме корней уравнения 4(2x + 5) - (x2
+ x + 20) = 0. Решим это уравнение: x2
- 7х = 0, x1
= 0, x2
= 7. Следовательно, решение неравенства можно записать в виде: х ≠ 0, х ≠ 7, или 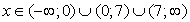 .
.
Пример 5.30.
Решение
Выполним последовательно пункты приведенной «инструкции»:
-
x2 + х - 6 = 0, x1 = -3, x2 = 2; x2 - 4х - 5 = 0, x1 = -1, x2 = 5.
Теперь можно разложить числитель и знаменатель на множители:
Видим, что в каждой найденной точке меняет знак ровно один из множителей, то есть меняет знак и вся дробь.
-
При х = 0 дробь принимает положительное значение. Расставим знаки на интервалах:
В ответе укажем промежутки, на которых дробь отрицательна. Не забудем учесть, что корни знаменателя в ответ никогда не входят (знаменатель не может равняться нулю), а корни числителя войдут в ответ, если неравенство нестрогое.
Ответ: [ -3; -1) U [2; 5).
Пример 5.31.
Решение
Выполним тождественные преобразования:
Корень числителя (х = -4)-кратный, так как при этом значении х ни один множитель не меняет знак. Корни знаменателя: х = -5 и х = -1. При х = 0 дробь положительна. Знаки на интервалах:
Заметим, что неравенство нестрогое, поэтому точка — 4 входит в ответ.
Ответ: (- ∞; -5) U (-1; ∞), x = -4.
Комментарий. Если для решения неравенства используется замена переменной, то важно не сделать раньше времени обратную замену. Сначала нужно полностью решить неравенство для вспомогательного неизвестного, найти его возможные значения (записав их не в интервальной форме, а в виде одного или нескольких неравенств), и только после этого подставить в эти неравенства выражение для вспомогательного неизвестного.
Пример 5.32.
Решение
Сделаем замену t = x2 - 7x + 17 и решим неравенство:
Его решение можно записать так: 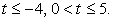 После обратной замены получим:
После обратной замены получим:
Дискриминант квадратного трехчлена, стоящего в левой части, отрицателен, следовательно, левая часть неравенства не может изменить знак, то есть сохраняет постоянный знак при любом значении х. Поскольку при х = 0 она отрицательна, то неравенство решений не имеет.
Первое неравенство верно всегда, решение второго: 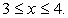 . Оно и будет окончательным ответом.
. Оно и будет окончательным ответом.
Ответ: [3; 4].
Пример 5.33.
Решить неравенство: (x2 - 3x + 2)(x2 - 9x + 20) < 180.
Решение
Разложим на множители оба квадратных трехчлена: (x - 1)(x - 2)(x - 4)(x - 5) < 180, и перемножим их в другом порядке (первый с последним и второй с третьим):
(x2 - 6x + 5)(x2 - 6x + 8) < 180.
Теперь можно сделать замену: t = x2 - 6x + 5, тогда:
t (t + 3) < 180, t2 + 3t - 180 < 0, (t + 15)(t - 12) < 0, -15 < t < 12.
Обратная замена:
Ответ: (-1; 7).
Пример 5.34.
Решить уравнение: x2 - 6x + 6 + | x — 6 | = 0.
Решение
Рассмотрим две возможности.
Случай 1. x - 6 ≥ 0, то есть х ≥ 6. Тогда | x — 6 | = x - 6, и уравнение принимает вид:
x2 - 6x + 6 + x - 6 = 0, x2 - 5х = 0, x1 = 5, x2 = 0.
Видим, что оба корня не соответствуют условию, поставленному на знак подмодульного выражения, следовательно, являются посторонними.
Случай 2. x - 6 < 0, x < 6; x2 - 6x + 6 - x + 6 = 0, x2 - 7x + 12 = 0, x1 = 3, x2 = 4 - оба корня соответствуют поставленному условию.
Ответ: х = 3, х = 4.
Комментарий. Аналогично решаются модульные неравенства этого типа, но если в уравнении достаточно проверить полученные корни на соответствие условию, задающему знак подмодульного выражения, то решением неравенства является объединение решений двух систем, состоящих из условия на знак подмодульного выражения и неравенства, полученного из исходного после раскрытия модуля.
Пример 5.35.
Случай 1. Пусть 4х + 5 ≥ 0, тогда нужно решить систему неравенств:
Решая второе неравенство методом интервалов, получим: 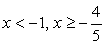
С учетом решения первого неравенства 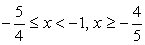 .
.
Объединяя решения обеих систем, находим окончательный ответ.
Комментарий. Процесс решения можно сократить в том случае, когда неизвестное входит только в подмодульное выражение. При этом обычно нет надобности исследовать знак этого выражения, так как его значение ограничивается конкретными числами.
Пример 5.36.
Решить уравнение: | x2 + 2x — 16 | = 8.
Решение
Выражение, модуль которого равен 8, может принимать только два значения: 8 и -8.
x2 + 2x - 16 = 8, x2 + 2x — 24 = 0, x1 = -6, x2 = 4.
x2 + 2x - 16 = -8, x2 + 2x - 8 = 0, x3 = -4, x4 = 2.
Отметим, что при таком способе решения не требуется проверка корней, так как среди них не может быть посторонних — при каждом из найденных значений х модуль выражения x2 + 2x — 16 равен 8.
Ответ: х = -6, х = - 4, х = 2, х = 4.
Пример 5.37.
Решить неравенство | | 2x - 3 | -7 | > 6.
Решение
Из неравенства | a | > b (при b > 0) следует, что a > b или a < -b. Рассмотрим эти случаи отдельно:
Вспомним, что неравенство | a | < b выполняется, если -b < a < b. Соответственно: 1 < 2x - 3 < 1, 2 < 2x < 4, 1 < x < 2.
Окончательным ответом будет объединение полученных решений.
Ответ: (- ∞; - 5) U (1; 2) U (8; + ∞).
Пример 5.38.
Решить уравнение: | x2 - 3x + 3 | = | 2x - 3 |.
Решение
Равенство | a | = | b | верно в двух случаях: a = b или a = -b. Применим это утверждение к решению уравнения:
x2 - 3x + 3 = 2x - 3, x2 - 5х + 6 = 0, x1 = 2, x2 = 3.
x2 - 3x + 3 = -2x + 3, x2 - х = 0, x3 = 0, x4 = 1.
Выбранный способ решения не приводит к появлению посторонних корней.
Ответ: х = 0, х = 1, х = 2, х = 3.
Комментарий. В уравнениях и неравенствах, в которые входит алгебраическая сумма нескольких модулей, можно «убрать» их все одновременно. Для этого достаточно найти корни каждого подмодульного выражения, отметить соответствующие точки на числовой прямой и получить интервалы, на каждом из которых все подмодульные выражения сохраняют постоянный знак. Определив эти знаки, мы можем заменить каждый модуль либо подмодульным выражением, либо выражением, противоположным ему.
Пример 5.39.
Решить уравнение | 2x + 2 | - | x | = x + 2.
Решение
Найдем корни подмодульных выражений: х = -1 и х = 0 и определим знаки этих выражений на интервалах (- ∞; - 1), (- 1; 0) и (0; + ∞) (для этого достаточно подставить в каждое подмодульное выражение вместо х какое-нибудь число из выбранного интервала):
На первом месте стоит знак первого подмодульного выражения, на втором — второго.
Теперь раскроем на каждом интервале оба модуля с учетом знака подмодульных выражений:
Найденный корень располагается на заданном интервале, следовательно, входит в ответ.
Точка 0 не включена в интервал, поэтому корень оказался посторонним.
Видим, что на этом промежутке уравнение превратилось в тождество, то есть его решением является любое значение х из рассматриваемого промежутка.
Ответ: х = -2, х ≥ 0.
Комментарий. Отметим две особенности уравнений такого типа, иллюстрацией которых может служить предыдущий пример: во-первых, решением такого уравнения может оказаться не конечный набор чисел, а непрерывный промежуток, и, во-вторых, вы можете включать точку, разделяющую интервалы, в любой из соседних промежутков. Если она не является решением уравнения, то ее включение в выбранный интервал не изменит набора корней, а если является, то этот корень обязательно получится в каждом из уравнений, к которым сводится исходное уравнение на соседних интервалах, и, соответственно, войдет в ответ.
Пример 5.40.
Решить неравенство | x + 5 | + | 2x - 3 | < 10.
Решение
Корни подмодульных выражений: х = -5 и х = 1,5. Расставим знаки этих выражений на полученных интервалах:
Последовательно решим три системы неравенств.
Объединим найденные решения: 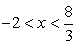 .
.
Пример 5.41.
Решить уравнение: x2 - 6x + | x - 3 | - 3 = 0.
Решение
Заметим, что 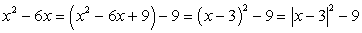 . Введем новое неизвестное t = | x - 3 | (t ≥ 0), тогда для t требуется решить уравнение t2
- 9 + t - 3 = 0, t2
+ t - 12 = 0, t1
= 3, t2
= - 4 < 0 — посторонний корень.
. Введем новое неизвестное t = | x - 3 | (t ≥ 0), тогда для t требуется решить уравнение t2
- 9 + t - 3 = 0, t2
+ t - 12 = 0, t1
= 3, t2
= - 4 < 0 — посторонний корень.
Следовательно: | x - 3 | = 3, x - 3 = ± 3, x1x1 = 0, x2 = 6.
Ответ: 0, 6.
Комментарий. Замена переменной применяется в модульных уравнениях и неравенствах заметно реже, чем в задачах других типов. Тем не менее, встречаются задания, в которых удобно сделать замену.
Как видим, такой способ решения намного короче и удобнее традиционного.
Пример 3.42.
Решить систему уравнений, содержащую модуль 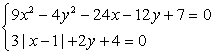 .
.
Решение
Случай 1. Пусть х ≥ 1, тогда система примет вид: 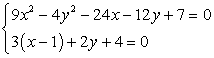 .
.
Сделаем подстановку из второго уравнения: 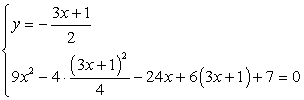
и упростим полученное уравнение для х:
9x2 - 9x2 - 6х - 1 - 24х + 18х + 6 + 7 = 0,12 - 12х = 0, х = 1, y = 2.
Случай 2. Если x < 1, то система выглядит так:
Тогда:
0 = 0 — тождество, то есть второе уравнение является верным равенством при любом x < 1, если у при этом связан с х соотношением 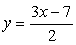 . Учитывая результат, полученный в пункте А, запишем окончательный ответ.
. Учитывая результат, полученный в пункте А, запишем окончательный ответ.
Пример 5.43.
Решение
Корни должны удовлетворять условию 4х - 8 ≥ 0, то есть х ≥ 2. Возведем обе части в квадрат:
Ответ: х = 3.
Пример 5.44.
Поскольку неизвестное входит в подкоренное выражение и в рациональную часть уравнения в виде одной и той же комбинации (x2
- 7х), можно сделать замену: 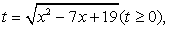 , тогда x2
- 7х = t2
- 19, и t определяется из уравнения: 2t + t2
- 19 + 4 = 0, t2
+ 2t — 15 = 0, t1
= 3, t2
= - 5 < 0 — не соответствует условию на знак t.
, тогда x2
- 7х = t2
- 19, и t определяется из уравнения: 2t + t2
- 19 + 4 = 0, t2
+ 2t — 15 = 0, t1
= 3, t2
= - 5 < 0 — не соответствует условию на знак t.
Обратная замена:
Ответ: х = 2, х = 5.
Комментарий. Замена переменной очень полезна при решении иррациональных уравнений. Часто с ее помощью удается избежать необходимости возведения в квадрат.
Пример 5.45.
Решение
Подкоренные выражения — взаимно обратные дроби, поэтому замена 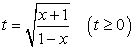 приводит к уравнению:
приводит к уравнению:
Комментарий. Следует обратить внимание на то, что в некоторых заданиях нет необходимости в проверке корней или задании каких-либо ограничений: значения х определяляются из условия, что корень принимает некоторое неотрицательное значение.
Пример 5.46.
Решение
Перепишем уравнение в виде: 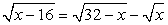 и возведем обе части в квадрат, не задавая никаких ограничений: проще будет в конце работы проверить получившиеся корни:
и возведем обе части в квадрат, не задавая никаких ограничений: проще будет в конце работы проверить получившиеся корни:
Еще раз возведем в квадрат обе части полученного равенства:
Проверка.
Ответ: х = 16.
Пример 5.47.
В этом уравнении замена 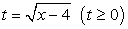 поможет ограничиться только одним возведением в квадрат:
поможет ограничиться только одним возведением в квадрат:
Пример 5.48.
Решение
ОДЗ задается условием: 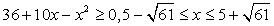 . Запишем уравнение в виде:
. Запишем уравнение в виде: 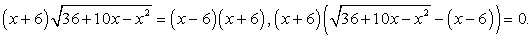
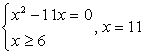 (корень первого уравнения х = 0 не удовлетворяет второму условию). Итак, единственный корень исходного уравнения — х = 11.
(корень первого уравнения х = 0 не удовлетворяет второму условию). Итак, единственный корень исходного уравнения — х = 11.
Ответ: х = 11.
Пример 5.49.
Вспомним свойства неравенств: если обе части неравенства неотрицательны, то при возведении в квадрат знак неравенства не меняется; если отрицательны, то знак меняется на противоположный; если же левая и правая части имеют разные знаки, то возведение в квадрат является некорректной операцией.
В данном неравенстве подкоренное выражение, разумеется, должно быть неотрицательным. Кроме того, значения правой части не меньше квадратного корня, то есть для решений неравенства правая часть может быть только неотрицательной. При выполнении этих условий мы имеем право возвести обе части в квадрат с сохранением знака неравенства:
Пересечение решений можно записать в виде: х ≥ 22.
Ответ: [22; + ∞).
Пример 5.50.
Решение
В этом неравенстве, в отличие от предыдущего, правая часть может принимать значения разных знаков. Рассмотрим эти случаи отдельно.
Случай 1. Если выполнены условия 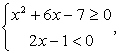 то неравенство будет верным: действительно, любое неотрицательное число больше любого отрицательного числа. Следовательно, все решения этой системы войдут в ответ. Решим полученную систему неравенств:
то неравенство будет верным: действительно, любое неотрицательное число больше любого отрицательного числа. Следовательно, все решения этой системы войдут в ответ. Решим полученную систему неравенств:
Случай 2. Вторая возможность — выполнение условий:
Пример 5.51.
Решение
Пусть 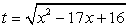 , тогда значения t определяются системой неравенств:
, тогда значения t определяются системой неравенств:
После обратной замены получим: 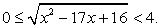 Поскольку левая и правая части этого двойного неравенства неотрицательны, мы можем возвести все три части в квадрат:
Поскольку левая и правая части этого двойного неравенства неотрицательны, мы можем возвести все три части в квадрат:
Ответ: (0; 1] U [16; 17).
Пример 5.52.
Решение
Во-вторых, 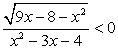 . Поскольку числитель дроби при всех допустимых значениях х неотрицателен, знаменатель должен принимать отрицательные значения, и неравенство сводится к системе:
. Поскольку числитель дроби при всех допустимых значениях х неотрицателен, знаменатель должен принимать отрицательные значения, и неравенство сводится к системе: 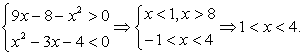
Объединяя найденные решения, получим окончательный ответ: 1 ≤ х < 4, x = 8.
Еще раз обратите внимание на то, что если бы мы не рассматривали случай равенства отдельно, а решали систему неравенств 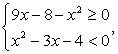 то потеряли бы решение х = 8.
то потеряли бы решение х = 8.
Ответ: [1; 4), x = 8.
Комментарий. Если корень четной степени входит в нестрогое неравенство в качестве множителя, то, чтобы избежать потери решений, лучше рассмотреть отдельно случай равенства и строгого неравенства.
 ,
,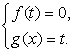
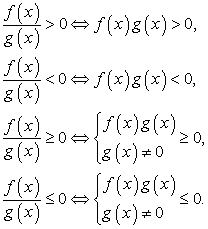
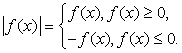
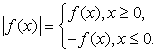
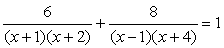
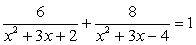
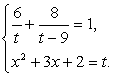
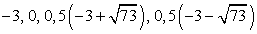
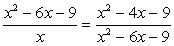 .
.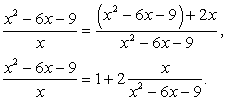
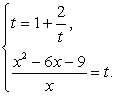
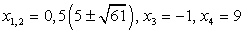
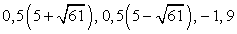
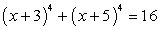
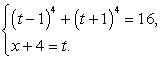
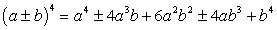
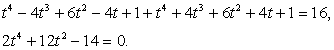
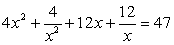
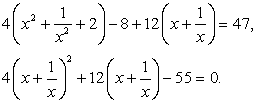
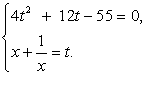 .
.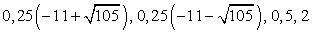
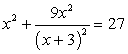
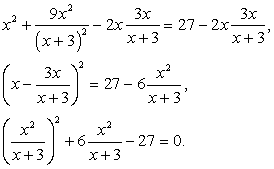
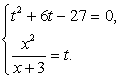
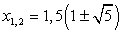
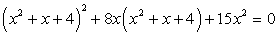
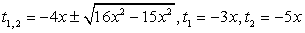
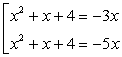
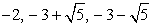
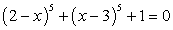
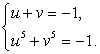
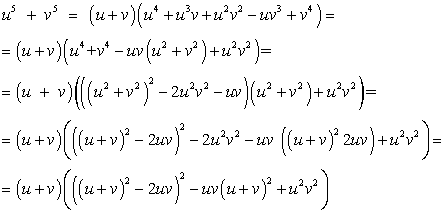 ,
,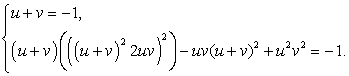
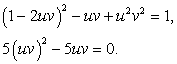
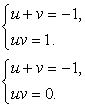
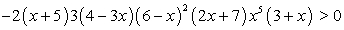
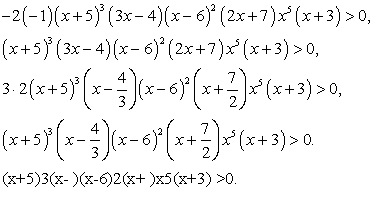


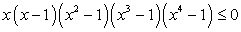
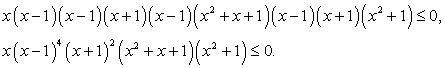

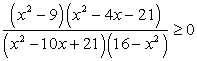
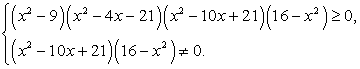
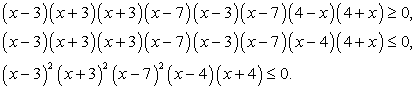

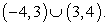


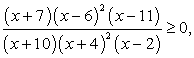
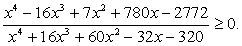
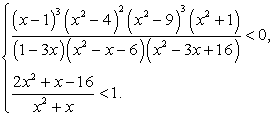
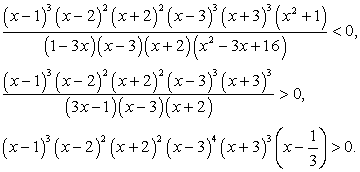
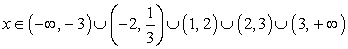
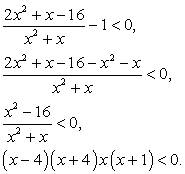


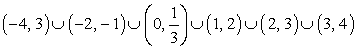
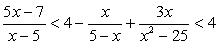 .
.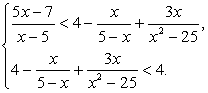
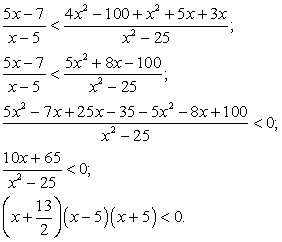

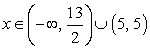
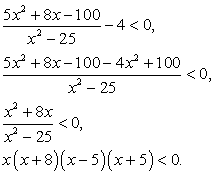
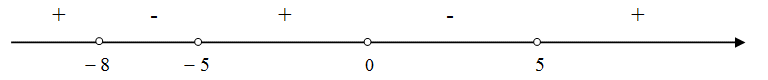

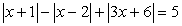
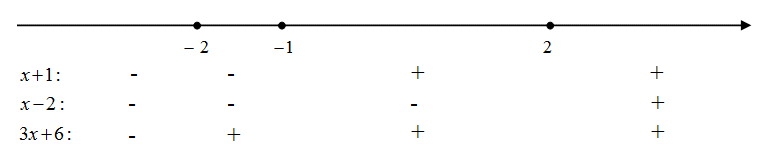
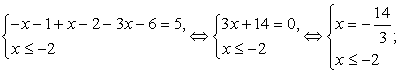
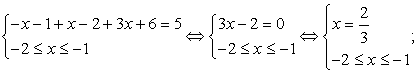
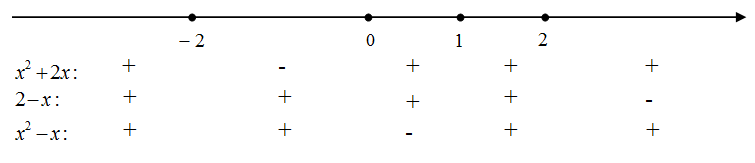
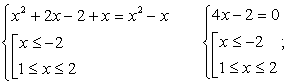
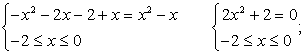
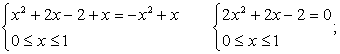
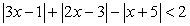
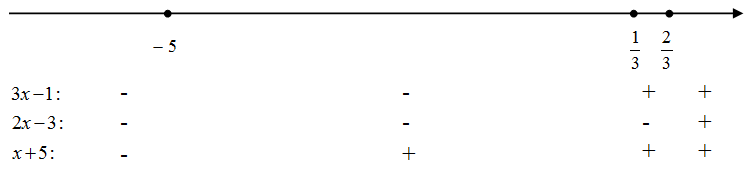
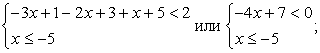
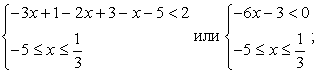
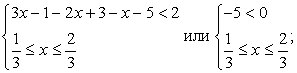
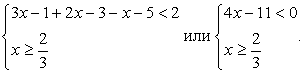
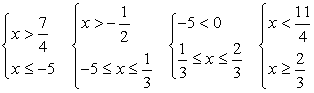
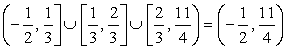
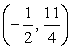
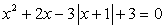 .
.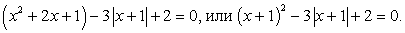
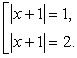
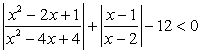 .
.
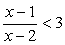 ;
;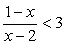 .
.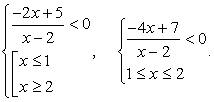
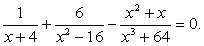
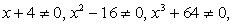 , откуда
, откуда 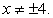
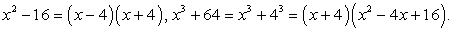
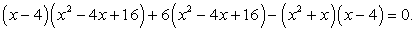
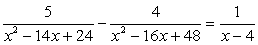 .
.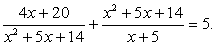
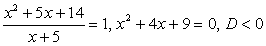 — нет решений;
— нет решений;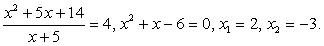
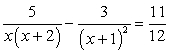 .
.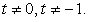
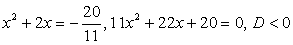 — решений нет.
— решений нет.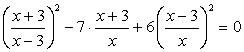 .
.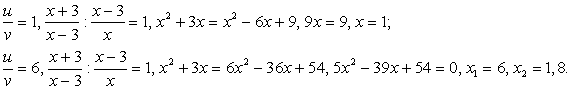
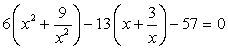 .
.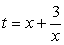 .
.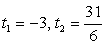
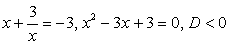 — решений нет.
— решений нет.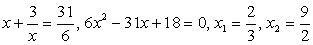 .
.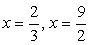 .
.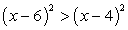 .
.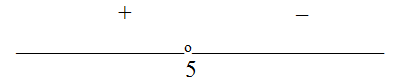
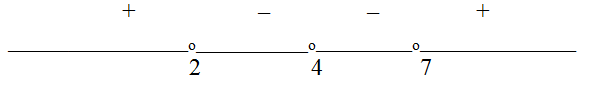
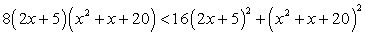
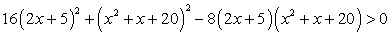
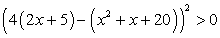
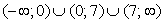 .
.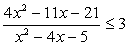 .
.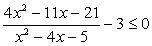 .
.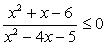 .
.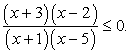
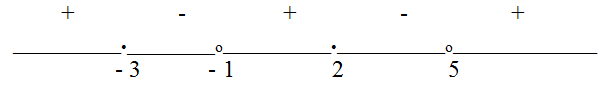
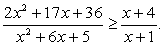
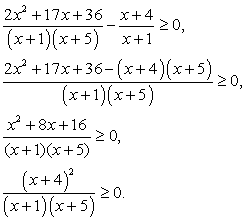
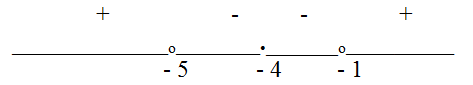
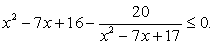
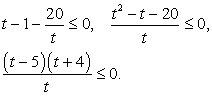
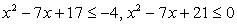 .
.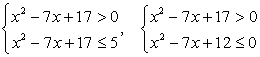 .
.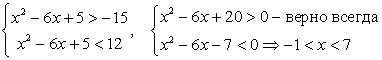 .
.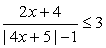 .
.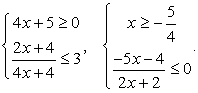 .
.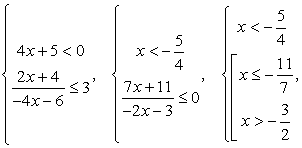
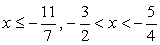 .
.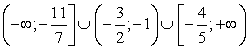
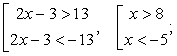
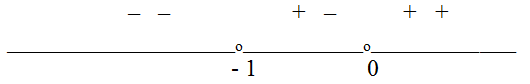
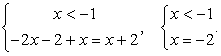
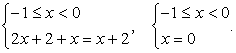
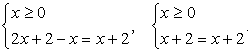
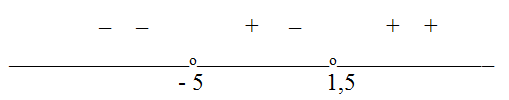
 — интервалы не пересекаются, решений нет.
— интервалы не пересекаются, решений нет.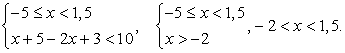 .
.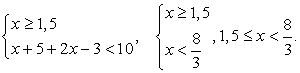 .
.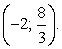
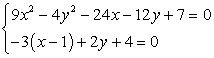 .
.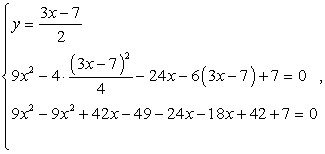
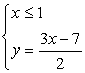 .
.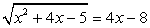 .
.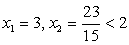 — посторонний корень.
— посторонний корень.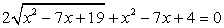 .
.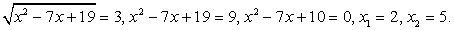
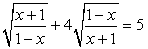 .
.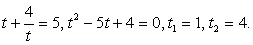
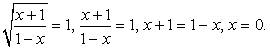
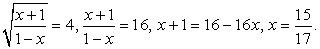
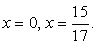
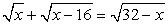 .
.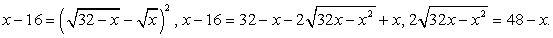
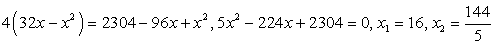 .
.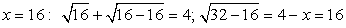 — корень уравнения.
— корень уравнения.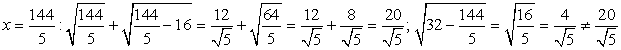 —
— 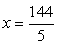 — не корень уравнения.
— не корень уравнения.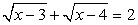 .
.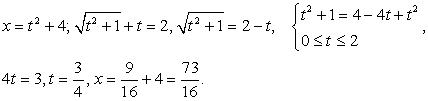
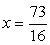 .
.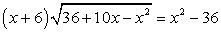 .
.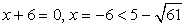 — посторонний корень.
— посторонний корень.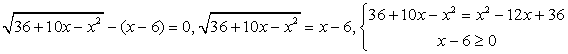 ,
,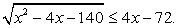
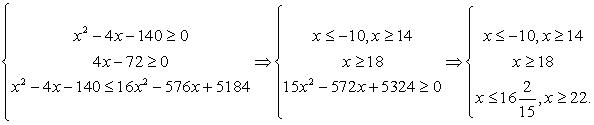
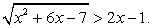
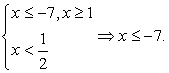
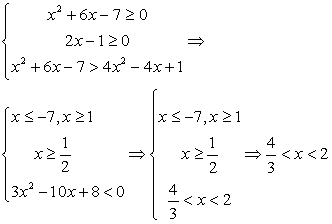 .
.