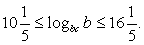Комментарий. Для выполнения заданий этой группы требуется хорошо знать свойства логарифмов и уметь их применять. Эта работа очень полезна для подготовки к решению логарифмических и показательных уравнений и неравенств. Рассмотрим далее задания, связанные с упрощением показательных и логарифмических выражений.
Формулы для справок
Вспомним основные свойства логарифмов.
-
Комментарий. Логарифм единицы по любому основанию равен нулю. Для того, чтобы убедиться в истинности данной формулы, достаточно вспомнить, что любое число (кроме нуля) в нулевой степени равно единице.
-
Комментарий. Логарифм равен единице в случае равенства чисел (выражений) — основания логарифма и выражения, стоящего под логарифмом.
-
Комментарий. Представленная формула является одним из вариантов записи определения логарифма.
-
Комментарий.
Данная формула называемая формулой перехода к новому основанию, имеет два важных следствия. Приравняем в формуле
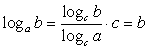 , тогда
, тогда 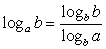 . Рассмотрим числитель полученной дроби. Поставим вопрос: в какую степень следует возвести число b, чтобы получить число b. Ответ — в первую степень, т.е. числитель рассматриваемой дроби равен единице. Таким образом,
. Рассмотрим числитель полученной дроби. Поставим вопрос: в какую степень следует возвести число b, чтобы получить число b. Ответ — в первую степень, т.е. числитель рассматриваемой дроби равен единице. Таким образом, 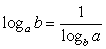 . В ряде задач полезно бывает полученную формулу записать в преобразованном виде:
. В ряде задач полезно бывает полученную формулу записать в преобразованном виде: 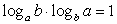 .
. -
Комментарий. Предполагается, что во всех представленных формулах параметры принимают допустимые значения.
Пример 3.1
Решение
Представим 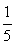 в виде степени числа 5, тогда
в виде степени числа 5, тогда 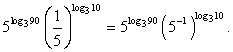
Далее воспользуемся правилом умножения степеней одинаковым основанием (при умножении степеней с одинаковым основанием показатели складываются):
Преобразуем полученную в процессе решения разность логарифмов (по одному основанию) и применим определение логарифма (зададим вопрос: В какую степень следует возвести основание логарифма 3, чтобы получить число, стоящее под логарифмом — 9?):
Ответ: 25.
Пример 3.2.
Решение
Упростим показатель степени подкоренного выражения: 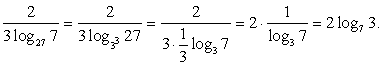
Тогда
Ответ: 27.
Пример 3.3.
Решение
Вначале упростим логарифмируемое выражение. Если Вы уже занимались упрощением алгебраических выражений, то вид первого множителя в знаменателе вызовет предположение, что перед нами полный квадрат. Действительно, 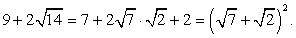 Тогда:
Тогда:
Ответ: 1/2.
Пример 3.4.
Решение
Разделим на знаменатель каждое слагаемое числителя по отдельности:
Переходя далее в каждом слагаемом к новому основанию 18, получаем, что:
Преобразуем далее сумму логарифмов с одинаковым основанием в логарифм произведения и используем определение логарифма:
Ответ: 1.
Пример 3.5.
Решение
Для преобразования данного выражения перейдем во всех логарифмах к основанию 4:
Тогда выражение принимает вид:
Далее разложим на множители логарифмируемые выражения, выделяя в каждом из них множитель вида 4n :
28 = 4 ∙ 7, 112 = 16 ∙ 7 = 42 ∙ 7, 448 = 64 ∙ 7 = 43 ∙ 7.
Продолжим преобразование выражения, используя свойства логарифмов:
Ответ: 2.
Пример 3.6.
Решение
Представим числа 2 и 1 в виде: 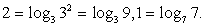 Тогда
Тогда 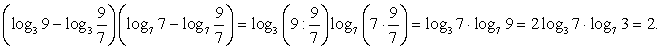
Ответ: 2.
Пример 3.7.
Решение
Обратим внимание на то, что в каждом логарифме (либо в основании, либо в аргументе) присутствует множитель 7. Поэтому перейдем к основанию 7 во всех логарифмах:
Обратим внимание, что 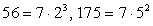 , тогда:
, тогда:
Следовательно, для вычисления этого логарифма нужно знать значения и 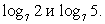 Воспользуемся формулами перехода к новому основанию:
Воспользуемся формулами перехода к новому основанию:
Подставим далее найденные значения в преобразованное исходное выражение:
Пример 3.8.
Известно, что 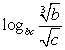 лежит между числами 8 и 13, а
лежит между числами 8 и 13, а 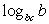 принимает целые значения. Найти количество этих значений.
принимает целые значения. Найти количество этих значений.
Решение
Перейдем в обоих логарифмах к основанию b.
Для этого воспользуемся сначала формулой «логарифм частного»: 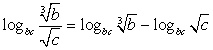 . Обратим далее внимание, что
. Обратим далее внимание, что 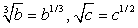 .
.
Получаем, что
Решим методом интервалов неравенство: 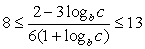 .
.
Для этого перейдем к систем нестрогих неравенств: 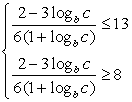 .
.
Рассматривая каждое из записанных неравенств отдельно и впоследствии находя решение как пересечение множеств (решений первого и второго неравенств), получаем: 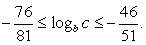
Выполним преобразования полученного двойного неравенства.
Прибавим 1 ко всем частям неравенства: 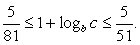 Поскольку
Поскольку 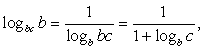 его значения задаются неравенством:
его значения задаются неравенством:
Следовательно, 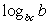 может принимать 6 целых значений – от 11 до 16.
может принимать 6 целых значений – от 11 до 16.
Ответ: 6.
 .
.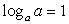 .
.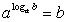 .
.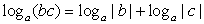 .
.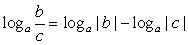 .
.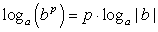 .
.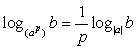 .
.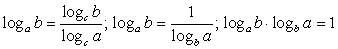 .
.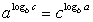 .
.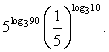
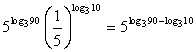 .
.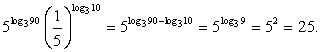
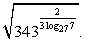
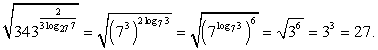
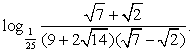
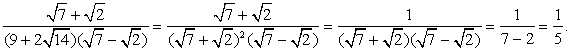
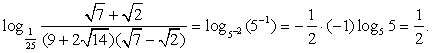
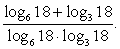
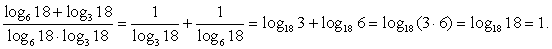
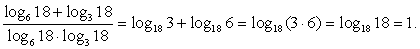
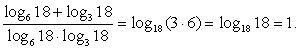
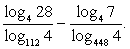
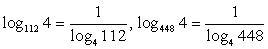 .
.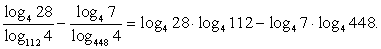
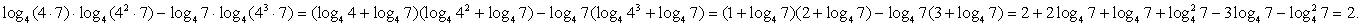
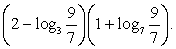
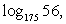 если
если 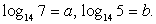
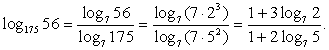
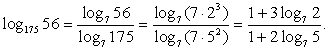
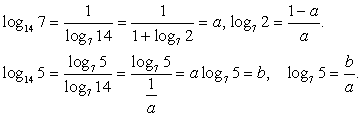
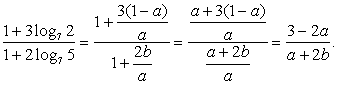
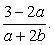
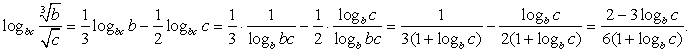
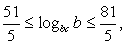 или
или