Цели обучения
В отличие от задачи, рассмотренной в предыдущей главе, мы имеем гипотезу, которую хотим апробировать на экспериментальных данных. Примеры некоторых гипотез:
-
новый дизайн упаковки ничем не лучше имеющегося;
-
новое лекарство не обладает преимуществами по сравнению с известными;
-
курящие люди не более склонны к сердечным заболеваниям, чем некурящие.
Изучив материал данной темы, Вы:
-
увидите, что методы проверки гипотез используют те же характеристики, что и методы построения доверительных интервалов, только с несколько иной точки зрения;
-
научитесь проверять, отвергается ли гипотеза имеющимися статистическими данными при заданном уровне значимости.
Удобнее обсуждать понятия на конкретном примере.
Пример
Менеджер ресторана недавно начал экспериментировать с новым способом приготовления пиццы. С его точки зрения, пицца, приготовленная новым способом, вкуснее, но для принятия окончательного решения о переходе на новый способ он хочет провести анализ мнения посетителей и планирует следующий эксперимент. Для 100 клиентов, заказавших пиццу на дом, он отправляет ее в двух вариантах приготовления и просит оценить в баллах свое мнение. Баллы от -10 до 10. Если клиент имеет сильное предпочтение к старому способу, то -10, к новому10, если все равно, то ноль и т.д. После сбора результатов какова должна быть процедура обработки?
Менеджер совсем не обязательно должен в данном случае использовать аппарат проверки гипотез. Но мы покажем, как он мог бы его использовать.
Нулевая и альтернативная гипотезы
Как правило, гипотезу, которую пытаются доказать, называют альтернативной , а которую опровергнуть — нулевой
, а которую опровергнуть — нулевой . Если обозначить в нашем примере среднее значение баллов как μ, то гипотезы могут быть записаны как:
. Если обозначить в нашем примере среднее значение баллов как μ, то гипотезы могут быть записаны как:
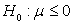 (нулевая гипотеза),
(нулевая гипотеза), 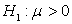 (альтернативная).
(альтернативная).
Односторонние и двусторонние тесты
Форма альтернативной гипотезы может быть односторонней или двусторонней, в зависимости, что хотят доказать. Если гипотеза может быть отвергнута результатами, как положительными, так и отрицательными, значит, мы имеем двусторонний случай, иначе односторонний.
Типы ошибок
В статистической теории проверки гипотез рассматривают ошибки двух типов.
Ошибка первого рода — отвергается истинная гипотеза.
Ошибка второго рода — не отвергается ложная гипотеза.
Уровень значимости и область отвержения гипотезы
Вероятность ошибки первого рода обычно обозначается α, называется уровнем значимости и принимает типичные значения 0,01 и 0,05. Задаваясь значением уровня значимости можно построить области, где гипотеза отвергается и не отвергается. Чем больше уровень значимости, тем больше вероятность ошибки первого рода и меньше вероятность ошибки второго рода и наоборот. Именно по этой причине выбор уровня значимости не является однозначным, а диктуется ситуацией и отношениям к ошибкам лица, принимающего решения (ЛПР).
и принимает типичные значения 0,01 и 0,05. Задаваясь значением уровня значимости можно построить области, где гипотеза отвергается и не отвергается. Чем больше уровень значимости, тем больше вероятность ошибки первого рода и меньше вероятность ошибки второго рода и наоборот. Именно по этой причине выбор уровня значимости не является однозначным, а диктуется ситуацией и отношениям к ошибкам лица, принимающего решения (ЛПР).
Вычисляем t-статистику.
Пример
Продолжим наш пример с менеджером ресторана (см. файл ПИЦЦА1.XLS (шаблон и решение
и решение ). Есть ли основание отвергать гипотезу (склонность к старому способу приготовления)?
). Есть ли основание отвергать гипотезу (склонность к старому способу приготовления)?
Решение
Напомним, что:
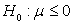 (нулевая гипотеза),
(нулевая гипотеза), 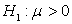 (альтернативная)
(альтернативная)
В нашем случае μ0 = 0. Вычисляем t-статистику: t = 2,816 (табл. 29).
Таблица 29.
Проверка гипотезы о предпочтении новому виду пиццы
Клиент |
Рейтинг |
|
|
1 |
-7 |
Рейтинг |
|
2 |
7 |
|
|
3 |
-2 |
Среднее |
2,1 |
4 |
4 |
Стандартная ошибка |
0,745757 |
5 |
7 |
Медиана |
2 |
6 |
6 |
Мода |
2 |
7 |
0 |
Стандартное отклонение |
4,716583 |
8 |
2 |
Дисперсия выборки |
22,24615 |
9 |
8 |
Эксцесс |
-0,84047 |
10 |
2 |
Асимметричность |
-0,21719 |
11 |
3 |
Интервал |
17 |
12 |
-4 |
Минимум |
-7 |
13 |
8 |
Максимум |
10 |
14 |
-5 |
Сумма |
84 |
15 |
7 |
Счет |
40 |
16 |
-5 |
|
|
Использование функции СТЬЮДРАСП(2,816;39;1) показывает, что для нулевой гипотезы вероятность результата составляет всего 0,4%. А следовательно, даже при уровне значимости 1% гипотеза должна быть отвергнута, то есть новый вид пиццы предпочтительнее.
Данная задача может быть решена и средствами StatPro, а именно c помощью StatPro/Statistical Inference/One-Sample Analysis. Соответствующее табло представлено на рис. 105 , а результаты на рис. 106
, а результаты на рис. 106 .
.
Результат проверки, как и следовало ожидать, получается эдентичный.
Проверка гипотез для различных параметров в своей основе аналогична тому, как исследовался вопрос о доверительных интервалах для различных параметров, так как используются те же распределения.
Проверка гипотез для доли совокупности
Выборочная доля имеет распределение, близкое к нормальному, поэтому вычисляем z-статистику по формуле:
Проверка гипотез для разности математических ожиданий
Вычисляется t-статистика по формулам:
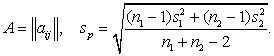
Проверка гипотез для разности между долями совокупности
Пусть 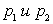 — значения долей, а
— значения долей, а 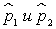 — их разностные оценки. Стандартное отклонение вычисляется по формуле:
— их разностные оценки. Стандартное отклонение вычисляется по формуле:
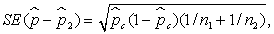
где 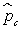 — выборочная пропорция, полученная по объединению выборок.
— выборочная пропорция, полученная по объединению выборок.
Далее используем функцию НОРМСТРАСП.
Литература
-
Wisniewski M. Quantitative Methods for Decision Makers / Mik Wisniewski. — Prentice Hall, 2002. — 575 с.
-
Айвазян С.А. Прикладная статистика и основы эконометрики: учебник / С.А. Айвазян, В.С. Мхитарян. — М.: ЮНИТИ, 1998. — 1022 с.
-
Карлберг К. Бизнес-анализ с помощью Excel: пер. с англ. / К. Карлберг. — Киев: Диалектика, 1997. — 448 с.
-
Макарова Н.В. Статистика в Excel / Н.В. Макарова, В.Я. Трофимец. — М.: Финансы и статистика, 2002. — 368 с.
-
Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде Excel: практикум / И.В. Орлова. — М.: Финстатинформ, 2000. — 136 с.
-
Томас Р. Количественные методы анализа хозяйственной деятельности: пер. с англ. / Ричард Томас. — М.: Дело и сервис, 1999. — 432 с.
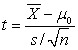
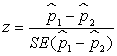 .
.
