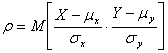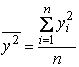4.2. Двумерная корреляционная модель

 

Рассмотрим случай изучения корреляционной зависимости между двумя признаками Y и X. Построение двумерной корреляционной модели предполагает, что закон распределения двумерной случайной величины в генеральной совокупности является нормальным, а выборка репрезентативной.

Плотность двумерного нормального закона распределения образуется формулой:

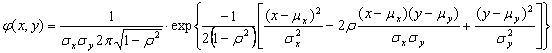
и определяется пятью параметрами:

МХ=mх	- математическое ожидание Х;
МY=my	- математическое ожидание Y;
DX=s2x	- дисперсия Х;
DY=s2y	- дисперсия Y;
	- парный коэффициент корреляции, характеризует тесноту линейной связи между величинами Х и Y.

 

В двумерной корреляционной модели используется так же, как мера тесноты связи, r² - коэффициент детерминации, указывающий долю дисперсии одной случайной величины, обусловленную вариацией другой.

Для получения точечных оценок параметров двумерной корреляционной модели обычно используют метод моментов, т.е. в качестве точечных оценок неизвестных начальных моментов первого и второго порядков генеральной совокупности берутся соответствующие выборочные моменты, и расчеты производят в соответствии со следующими формулами:

	- оценка для mх;
	- оценка для mу;
	- оценка для М(X2);
	- оценка для М(Y2);
	- оценка для М(XY);
	- оценка для sх2;
	- оценка для sу2;
	- оценка для r.

 

Полученные оценки являются состоятельными, а  также обладают свойствами несмещенности и эффективности. Следует отметить, что в корреляционной модели распределение выборочных средних  не зависит от законов распределения S²_x, S²_y, r.

        

Парный коэффициент корреляции rв силу своих свойств является одним из самых распространенных способов измерения связи между случайными величинами в генеральной совокупности; для выборочных данных используется эмпирическая мера связи r.

Коэффициент корреляции не имеет размерности и, следовательно, его можно сопоставлять для разных статистических рядов. Величина его лежит в пределах (-1 до +1). Значение r=±1 свидетельствует о наличии функциональной зависимости между рассматриваемыми признаками. Если r=0, можно сделать вывод, что линейная связь  между х и у отсутствует, однако это не означает, что они статистически независимы. В этом случае не отрицается возможность существования иной формы зависимости между переменными. Положительный знак коэффициента корреляции указывает на положительную корреляцию, т.е. все данные наблюдения лежат вблизи прямой  с положительным углом наклона в плоскости ху и с увеличением х растет у. Когда х уменьшается, то у уменьшается. Отрицательный знак коэффициента свидетельствует об отрицательной корреляции. Чем ближе значение |r|к единице, тем связь теснее, приближение |r|к нулю означает ослабление линейной зависимости между переменными. При |r|=1 корреляционная связь перерождается в функциональную.

        

На практике при изучении зависимости между двумя случайными величинами используют «поле корреляции», с помощью которого при минимальных затратах труда и времени можно установить наличие корреляционной зависимости.

         Поле корреляции представляет собой диаграмму, на которой изображается совокупность значений двух признаков. Каждая точка этой диаграммы имеет координаты (x_i, y_i), соответствующие размерам признаков в i-м наблюдении. Три варианта распределения точек на поле корреляции показаны на рисунках 1.4.1; 1.4.2; 1.4.3. На первом из них основная масса точек укладывается в эллипсе, главная диагональ которого образует положительный угол с осью Х. Это график положительной корреляции. Второй вариант распределения соответствует отрицательной корреляции. Равномерное распределение точек в пространстве (ХУ) свидетельствует об отсутствии корреляционной зависимости (рис. 1.4.3.).

 

 

Если наблюдаемые значения У и Х представляют собой выборку из двумерного нормального распределения, то формально можно рассматривать два уравнения регрессии:

.

В двумерном корреляционном анализе, обычно строят корреляционную таблицу, поле корреляции, рассчитывают точечные оценки параметров корреляционной модели, оценивают уравнения регрессии, проверяют значимость параметров связи и для значимых параметров строят интервальные оценки, не разделяя при этом задачи корреляционного  и регрессионного анализа.

Имея оценки параметров модели  можно рассчитать оценки уравнений регрессии в соответствии с формулой для генеральной регрессии:

 

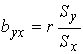где - коэффициент регрессии у на х, оценка здесь  где  - оценка генерального коэффициента регрессии b_ух.

Аналогичные формулы расчета справедливы для оценки уравнения регрессии х на у:

 

 - генеральная регрессия х на у,

где 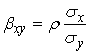- коэффициент регрессии х на у,

 - где  - оценка генерального коэффициента регрессии b_ху.

Можно показать, что формулы  и  идентичны. Из формулы:

полагая, что b_ух=b₁, а -b_ухМ(х)+М(у)= b₀, запишем: .

Аналогично можно показать идентичность формул попарно:

 

 

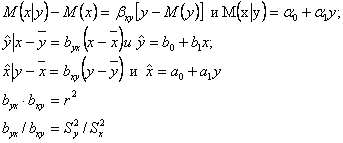
В двумерной модели параметрами связи являются коэффициент корреляции r (или коэффициент детерминации r²) и коэффициенты регрессии b_ух, b_ху, которые обычно бывают неизвестны.

По результатам выборки рассчитывают их точечные оценки, cоответственно r, b_y, b_x, проверяют гипотезу о значимости (существенности) параметров. В двумерной модели достаточно проверить значимость только коэффициента корреляции. Проверяется гипотеза Н₀: r=0. Если на уровне значимости a гипотеза отвергнется, то коэффициент корреляции считается значимым и рассчитанное по выборке значение r может быть использовано в качестве его точечной оценки. Если коэффициент корреляции оказывается незначимым, то гипотеза не отвергается и на практике обычно принимают, что х и у в генеральной совокупности линейно независимы.

Доказано, что если верна гипотеза Н₀: r=0, то статистика  имеет распределение Стьюдента с n=n-2числом степеней свободы. По таблице распределения Стьюдента были определены значения статистики t_табл(a;n=n-2) для a=0,001; 0,01; 0,02; 0,05 и рассчитаны соответственно границы дляr(таблицa Фишера-Иейтса). Таким образом, для  проверки гипотезы Н₀: r=0, находят r_табл(a, n=n-2) и сравнивают его с r_набл, рассчитанным по выборочным данным. Если |r_набл.|³r_табл, то гипотеза Н₀ отвергается на уровне значимости a, если |r_набл.|r_табл, то гипотеза не отвергается.

При n>100, считая распределение статистики нормированным нормальным, проверяют гипотезу Н₀: r=0, исходя из условия, что при справедливой гипотезе выполняется равенство: P(|t|t_табл)=g=Ф(t_табл),

т.е. если |t|t_табл, то гипотеза Н₀ не отвергается. Статистика , если n>100, также имеет нормированный нормальный закон распределения при справедливости Н₀: r=0 и этим можно пользоваться для проверки значимости коэффициента корреляции.

Для двумерной корреляционной модели, если отвергается гипотеза Н₀: r=0, то параметры связи r, b_ух, b_ху считаются значимыми и для них имеет смысл найти интервальные оценки, для чего нужно знать закон распределения выборочных оценок параметров.

Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому используют специально подобранные функции от выборочного коэффициента корреляции, которые подчиняются хорошо изученным законам, например, нормальному или Стьюдента.

При нахождении доверительного интервала для коэффициента корреляции r чаще используют преобразование Фишера:

.

Эта статистика уже при n>10 распределена приблизительно нормально, с параметрами .

По таблице z - преобразования Фишера для выборочного коэффициента rнаходят соответствующее ему z_rи находят интервальную оценку для M(z)из условия:

,

 

где t_gнаходят по таблице интегральной функции Лапласа:

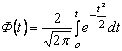 для данного g=1-a.

Получив  доверительный интервал: , с помощью таблицы z - преобразования Фишера получают интервальную оценку: , где r_minи r_max выбираются с учетом того, что z- функция нечетная, а поправочным членом  пренебрегают.

Для значимых коэффициентов регрессии b_ух и b_ху с надежностью  g=1-a, находят интервальные оценки из условия, что статистики:

имеют распределение Стьюдента с n=n-2степенями свободы и, следовательно, из условия Р(|t|<=t_a)=gможно рассчитать интервальные оценки:

 

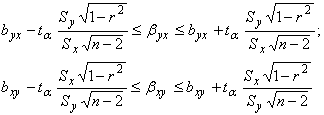
где t_aопределяется по таблице Стьюдента для данного a=1-g и n=n-2.

 

Пример 4.1. На основании выборочных данных о производительности труда (х) и себестоимости продукции (у), полученных с однотипных предприятий за месяц и представленных в таблице 4.1, найти: а) точеную оценку коэффициента корреляции между х и у, проверить его значимость при a=0,05 и найти интервальную оценку коэффициента корреляции при g=0,95; б) оценку уравнения регрессии, характеризующего зависимость себестоимости продукции от производительности труда.

Таблица 4.1

 

производительность труда х	5	4	3	20	10	15
себестоимость продукции у	7	10	12	2	5	4

 

Решение

Составим вспомогательную таблицу 4.2

 

Таблица 4.2

 

	xi	yi	xiyi	xi2	yi2
	5	7	35	25	49
	4	10	40	16	100
	3	12	36	9	144
	20	2	40	400	4
	10	5	50	100	25
	15	4	60	225	16
S	57	40	261	775	338
средние	9,5	6,67	43,5	129,17	56,33

 

а) Выборочный парный коэффициент корреляции рассчитывается по формуле:

 

,

 

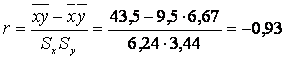где

.

 

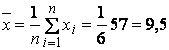
Для проверки значимости  коэффициента корреляции сформулируем статистическую гипотезу Н₀: r=0. По таблице Фишера-Йейтса  находим r_табл (a=0,05; u=n-2=4)=0,811. Сравнение çr_набл ç=0,93 с r_табл=0,811 свидетельствует о том, что нулевая гипотеза отвергается и, следовательно, коэффициент корреляции r значим.

Интервальную оценку для r рассчитаем с помощью z - преобразований Фишера. По таблице значений статистики  находим z_r=0,93. Из условия, что g=Ф(t_g)=0,95, находим по таблице интегральной функции Лапласа t_g=1,96. Тогда интегральная оценка для MZ_r определяется: Z(r=0,93)=1,6584

 

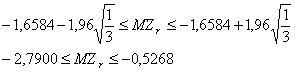
         Воспользовавшись таблицей z - преобразования Фишера, перейдем от z  к  r и найдем интегральную оценку с надежностью g=0,95:

.

 

б) Для нахождения оценок уравнения регрессии себестоимости продукции от производительности труда =b₀+b₁x, воспользуемся формулой:

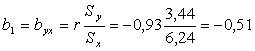
b₀=6,67-(-0,51)9,5=11,52.

Тогда используя , находим:

.

 

 

К оглавлению

Назад к разделу "4. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ"

Вперед к разделу "4.3. Трехмерная корреляционная модель"