3.2. Распределение Фишера-Снедекора

 

Во многих задачах математической статистики, особенно в дисперсионном анализе в проверке статистических гипотез, важную роль играет   F - распределение. Это распределение отношения двух выборочных дисперсий впервые было исследовано английским статистиком P. Фишером. Однако оно нашло широкое применение в статистических исследованиях лишь после того, как американский статистик Дж. Снедекор составил таблицы для данного распределения. В этой связи           F - распределение называют распределением Фишера-Снедекора.

Пусть имеем две независимые случайные величины X и Y, подчиняющиеся нормальному закону распределения. Произведены две независимые выборки объемами n₁ и n₂, и вычислены выборочные дисперсии  и . Известно, что случайные величины 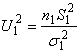 и 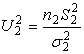 имеют c² - распределение с соответственно n₁ = n₁ - 1 и n₂ = n₂ - 1 степенями свободы. Случайная величина:

 

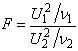                                                                                                                   (3.5)

имеет F - распределение с n₁ и n₂степенями свободы. Причем , так что F ³ 1.

Закон распределения случайной величины F не зависит от неизвестных параметров  и  а зависит лишь от числа наблюдений в выборках n₁ и n₂. Составлены таблицы распределения случайной величины F, в которых различным значениям уровня значимости a и различным сочетаниям величин n₁ и n₂ соответствуют такие значения F(a,n₁, n₂), для которых справедливо равенство P[F > F(a,n₁, n₂)] = a.

 

 

К оглавлению

Назад к разделу "3. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ"

Вперед к разделу "3.3. Гипотезы о генеральных средних нормально распределенных совокупностей"