Глава 4. Доверительные интервалы прогноза. Оценка адекватности и точности моделей

§ 4.1. Доверительные интервалы прогноза

Заключительным этапом применения кривых роста является экстраполяция тенденции на базе выбранного уравнения. Прогнозные значения исследуемого показателя вычисляют путем подстановки в уравнение кривой значений времени t, соответствующих периоду упреждения. Полученный таким образом прогноз называют точечным, так как для каждого момента времени определяется только одно значение прогнозируемого показателя.

На практике в дополнении к точечному прогнозу желательно определить границы возможного изменения прогнозируемого показателя, задать "вилку" возможных значений прогнозируемого показателя, т.е. вычислить прогноз интервальный.

Несовпадение фактических данных с точечным прогнозом, полученным путем экстраполяции тенденции по кривым роста, может быть вызвано:

1) субъективной ошибочностью выбора вида кривой;

2) погрешностью оценивания параметров кривых;

3) погрешностью, связанной с отклонением отдельных наблюдений от тренда, характеризующего некоторый средний уровень ряда на каждый момент времени.

Погрешность, связанная со вторым и третьим источником, может быть отражена в виде доверительного интервала прогноза. Доверительный интервал, учитывающий неопределенность, связанную с положением тренда, и возможность отклонения от этого тренда, определяется в виде:

(4.1.),

где n - длина временного ряда;

L -период упреждения;

-точечный прогноз на момент n+L;

- значение t-статистики Стьюдента;

- средняя квадратическая ошибка прогноза.

Предположим, что тренд характеризуется прямой:

Так как оценки параметров определяются по выборочной совокупности, представленной временным рядом, то они содержат погрешность. Погрешность параметра приводит к вертикальному сдвигу прямой, погрешность параметра - к изменению угла наклона прямой относительно оси абсцисс. С учетом разброса конкретных реализаций относительно линий тренда, дисперсию можно представить в виде:

(4.2.),

где - дисперсия отклонений фактических наблюдений от расчетных;

- время упреждения, для которого делается экстраполяция;

= n + L ;

t- порядковый номер уровней ряда, t=1,2, ... , n;

- порядковый номер уровня, стоящего в середине ряда,

=(n+1):2

Тогда доверительный интервал можно представить в виде:

(4.3.)

Обозначим корень в выражении (4.3.) через К. Значение К зависит только от n и L, т.е. от длины ряда и периода упреждения. Поэтому можно составить таблицы значений К или К*= t_aK . Тогда интервальная оценка будет иметь вид:

(4.4.)

Выражение, аналогичное (4.3.), можно получить для полинома второго порядка:

(4.5.)

или

(4.6.)

Дисперсия отклонений фактических наблюдений от расчетных определяется выражением:

(4.7.),

где - фактические значения уровней ряда,

- расчетные значения уровней ряда,

n- длина временного ряда,

k - число оцениваемых параметров выравнивающей кривой.

Таким образом, ширина доверительного интервала зависит от уровня значимости, периода упреждения, среднего квадратического отклонения от тренда и степени полинома.

Чем выше степень полинома, тем шире доверительный интервал при одном и том же значении , так как дисперсия уравнения тренда вычисляется как взвешенная сумма дисперсий соответствующих параметров уравнения

Рисунок 4.1. Доверительные интервалы прогноза для линейного тренда

Доверительные интервалы прогнозов, полученных с использованием уравнения экспоненты, определяют аналогичным образом. Отличие состоит в том, что как при вычислении параметров кривой, так и при вычислении средней квадратической ошибки используют не сами значения уровней временного ряда, а их логарифмы.

По такой же схеме могут быть определены доверительные интервалы для ряда кривых, имеющих асимптоты, в случае, если значение асимптоты известно (например, для модифицированной экспоненты).

В таблице 4.1. приведены значения K* в зависимости от длины временного ряда n и периода упреждения L для прямой и параболы. Очевидно, что при увеличении длины рядов (n) значения K* уменьшаются, с ростом периода упреждения L значения K* увеличиваются. При этом влияние периода упреждения неодинаково для различных значений n: чем больше длина ряда, тем меньшее влияние оказывает период упреждения L.

Таблица 4.1.

Значения К* для оценки доверительных интервалов прогноза на основе линейного тренда и параболического тренда при доверительной вероятности 0,9 (7).

Линейный тренд

Параболический тренд

Длина ряда (n)

Период упреждения (L)

123

длина ряда (n)

период упреждения (L)

123

2,6380 2,8748 3,1399

2,4631 2,6391 2,8361

2,3422 2,4786 2,6310

2,2524 2,3614 2,4827

2,1827 2,2718 2,3706

2,1274 2,2017 2,2836

2,0837 2,1463 2,2155

2,0462 2,1000 2,1590

2,0153 2,0621 2,1131

1,9883 2,0292 2,0735

1,9654 2,0015 2,0406

1,9455 1,9776 2,0124

1,9280 1,9568 1,9877

1,9117 1,9375 1,9654

1,8975 1,9210 1,9461

1,8854 1,9066 1,9294

1,8738 1,8932 1,9140

1,8631 1,8808 1,8998

1,8538 1,8701 1,8876

3,948 5,755 8,152

3,459 4,754 6,461

3,144 4,124 5,408

2,926 3,695 4,698

2,763 3,384 4,189

2,636 3,148 3,808

2,536 2,965 3,516

2,455 2,830 3,286

2,386 2,701 3,100

2,330 2,604 2,950

2,280 2,521 2,823

2,238 2,451 2,717

2,201 2,391 2,627

2,169 2,339 2,549

2,139 2,293 2,481

2,113 2,252 2,422

2,090 2,217 2,371

2,069 2,185 2,325

2,049 2,156 2,284

§ 4.2. Проверка адекватности выбранных моделей

Проверка адекватности выбранных моделей реальному процессу (в частности, адекватности полученной кривой роста) строится на анализе случайной компоненты. Случайная остаточная компонента получается после выделения из исследуемого ряда систематической составляющей (тренда и периодической составляющей, если она присутствует во временном ряду). Предположим, что исходный временной ряд описывает процесс, не подверженный сезонным колебаниям, т.е. примем гипотезу об аддитивной модели ряда вида:

(4.8.)

Тогда ряд остатков будет получен как отклонения фактических уровней временного ряда () от выравненных, расчетных ():

(4.9.)

При использовании кривых роста вычисляют, подставляя в уравнения выбранных кривых соответствующие последовательные значения времени.

Принято считать, что модель адекватна описываемому процессу, если значения остаточной компоненты удовлетворяют свойствам случайности, независимости, а также случайная компонента подчиняется нормальному закону распределения.

При правильном выборе вида тренда отклонения от него будут носить случайный характер. Это означает, что изменение остаточной случайной величины не связано с изменением времени. Таким образом, по выборке, полученной для всех моментов времени на изучаемом интервале, проверяется гипотеза о зависимости последовательности значений от времени, или, что то же самое, о наличии тенденции в ее изменении. Поэтому для проверки данного свойства может быть использован один из критериев, рассматриваемых в разделе I, например, критерий серий.

Если вид функции, описывающей систематическую составляющую, выбран неудачно, то последовательные значения ряда остатков могут не обладать свойствами независимости, т.к. они могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция ошибок.

В условиях автокорреляции оценки параметров модели, полученные по методу наименьших квадратов, будут обладать свойствами несмещенности и состоятельности (с этими свойствами знакомятся в курсе математической статистики). В то же время эффективность этих оценок будет снижаться, а, следовательно, доверительные интервалы будут иметь мало смысла в силу своей ненадежности.

Существует несколько приемов обнаружения автокорреляции. Наиболее распространенным является метод, предложенный Дарбиным и Уотсоном. Критерий Дарбина-Уотсона связан с гипотезой о существовании автокорреляции первого порядка, т.е. автокорреляции между соседними остаточными членами ряда. Значение этого критерия определяется по формуле:

(4.10.)

Можно показать, что величина d приближенно равна:

d»2(1-) (4.11),

где - коэффициент автокорреляции первого порядка (т.е. парный коэффициент корреляции между двумя рядами и ).

Из последней формулы видно, что если в значениях имеется сильная положительная автокорреляция (»1), то величина d=0 , в случае сильной отрицательной автокорреляции (»-1) d=4. При отсутствии автокорреляции (»0) d=2.

Для этого критерия найдены критические границы, позволяющие принять или отвергнуть гипотезу об отсутствии автокорреляции. Авторами критерия границы определены для 1, 2,5 и 5% уровней значимости .Значения критерия Дарбина-Уотсона при 5% уровне значимости приведены в таблице 4.2. В этой таблице и - соответственно нижняя и верхняя доверительные границы критерия Дарбина-Уотсона; - число переменных в модели; n - длина временного ряда.

Таблица 4.2.

Значения критерия Дарбина-Уотсона d₁ и d₂ при 5% уровне значимости

1,08

1,1

1,13

1,16

1,18

1,2

1,22

1,”4

1,26

1,27

1,29

1,3

1,32

1,33

1,34

1,35

1,36

1,37

1,38

1,49

1,4

1,41

1,36

1,37

1,38

1,39

1,4

1,41

1,42

1,43

1,44

1,45

1,46

1,47

1,48

1,49

1,5

1,51

1,52

0,95

0,98

1,02

1,05

1,08

1,1

1,13

1,15

1,17

1,19

1,21

1,22

1,24

1,26

1,27

1,28

1,3

1,31

1,32

1,33

1,34

1,35

1,54

1,53

1,54

1,55

1,56

1,57

1,58

1,59

0,82

0,86

0,9

0,93

0,97

1,03

1,05

1,08

1,1

1,12

1,14

1,16

1,18

1,2

1,21

1,23

1,24

1,26

1,27

1,28

1,29

1,75

1,73

1,71

1,69

1,68

1,67

1,66

1,65

Применение на практике критерия Дарбина-Уотсона основано на сравнении величины d, рассчитанной по формуле (4.10.), с теоретическими значениями d₁ и d₂, взятыми из таблицы. Отметим, что большинство программных пакетов статистической обработки данных осуществляет расчет этого критерия (например, ППП "Олимп", "Мезозавр", "Statistica" и др.).

При сравнении величины d с и возможны следующие варианты:

1) Если d < , то гипотеза о независимости случайных отклонений (отсутствие автокорреляции) отвергается;

2) Если d > , то гипотеза о независимости случайных отклонений не отвергается;

3) Если £ d£ , то нет достаточных оснований для принятия решений, т.е. величина попадает в область "неопределенности".

Рассмотренные варианты относятся к случаю, когда в остатках имеется положительная автокорреляция.

Когда же расчетное значение d превышает 2, то можно говорить о том, что в существует отрицательная автокорреляция.

Для проверки отрицательной автокорреляции с критическими значениями и сравнивается не сам коэффициент d, а 4-d.

Для определения доверительных интервалов модели свойство нормальности распределения остатков имеет важное значение. Поскольку временные ряды экономических показателей, как правило, невелики (<50), то проверка распределения на нормальность может быть произведена лишь приближенно, например, на основе исследования показателей асимметрии и эксцесса.

При нормальном распределении показатели асимметрии (А) и эксцесса (Э) равны нулю. Так как мы предполагаем, что отклонения от тренда представляют собой выборку из некоторой генеральной совокупности, то можно определить выборочные характеристики асимметрии и эксцесса, а также их среднеквадратические ошибки.

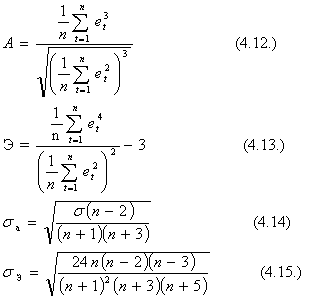
где А - выборочная характеристика асимметрии;

Э- выборочная характеристика эксцесса;

- среднеквадратическая ошибка выборочной характеристики асимметрии;

- среднеквадратическая ошибка выборочной характеристики эксцесса.

Если одновременно выполняются следующие неравенства:

|A|<1,5; |Э+|<1,5(4.16.),

то гипотеза о нормальном характере распределения случайной компоненты не отвергается.

Если выполняется хотя бы одно из неравенств

(4.17.),

то гипотеза о нормальном характере распределения отвергается.

Другие случаи требуют дополнительной проверки с помощью более мощных критериев.

Пример 4.1.

Программа выдала следующие характеристики ряда остатков:

длина ряда n=20;

коэффициент асимметрии А=0,6;

Коэффициент эксцесса Э=0,7.

На основании этих характеристик можно считать, что:

а) случайная компонента подчиняется нормальному закону распределения;

б) случайная компонента не подчиняется нормальному закону распределения;

в) требуется дополнительная проверка характера распределения случайной компоненты.

Решение:

Определим:

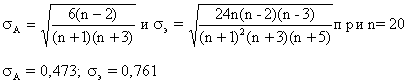
Т. к. одновременно выполняются оба неравенства

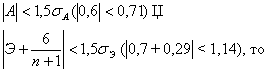
можно считать, что случайная компонента подчиняется нормальному закону распределения - вариант ответа а).

§ 4.3. Характеристики точности моделей

Важнейшими характеристиками качества модели, выбранной для прогнозирования, являются показатели ее точности. Они описывают величины случайных ошибок, полученных при использовании модели. Таким образом, чтобы судить о качестве выбранной модели, необходимо проанализировать систему показателей, характеризующих как адекватность модели, так и ее точность.

О точности прогноза можно судить по величине ошибки (погрешности) прогноза.

Ошибка прогноза - величина, характеризующая расхождение между фактическим и прогнозным значением показателя.

Абсолютная ошибка прогноза определяется по формуле:

- (4.18.),

где - прогнозное значение показателя,

- фактическое значение.

Эта характеристика имеет ту же размерность, что и прогнозируемый показатель и зависит от масштаба измерения уровней временного ряда.

На практике широко используется относительная ошибка прогноза, выраженная в процентах относительно фактического значения показателя:

(4.19.)

Также используются средние ошибки по модулю (абсолютные и относительные):

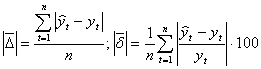(4.20.),

где n- число уровней временного ряда, для которых определялось прогнозное значение.

Из (4.18.), (4.19.) видно, что если абсолютная и относительная ошибка больше 0, то это свидетельствует о "завышенной" прогнозной оценке, если - меньше 0, то прогноз был занижен.

Очевидно, что все указанные характеристики могут быть вычислены после того, как период упреждения уже окончился, и имеются фактические данные о прогнозируемом показателе или при рассмотрении показателя на ретроспективном участке.

В последнем случае имеющаяся информация делится на две части: по первой - оцениваются параметры модели, а данные второй части рассматриваются в качестве фактических. Ошибки прогнозов, полученные ретроспективно (на втором участке) характеризуют точность применяемой модели.

На практике при проведении сравнительной оценки моделей могут использоваться такие характеристики качества как дисперсия () или среднеквадратическая ошибка прогноза (S):

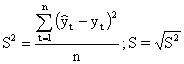(4.21.).

Чем меньше значения этих характеристик, тем выше точность модели.

О точности модели нельзя судить по одному значению ошибки прогноза. Например, если прогнозная оценка месячного уровня производства в июне совпала с фактическим значением, то это не является достаточным доказательством высокой точности модели. Надо учитывать, что единичный хороший прогноз может быть получен и по плохой модели, и наоборот.

Следовательно, о качестве применяемых моделей можно судить лишь по совокупности сопоставлений прогнозных значений с фактическими.

Простой мерой качества прогнозов может стать m-относительное число случаев, когда фактическое значение охватывалось интервальным прогнозом:

(4.22.),

где р - число прогнозов, подтвержденных фактическими данными;

q - число прогнозов, не подтвержденных фактическими данными.

Когда все прогнозы подтверждаются, q=0 и m=1.

Если же все прогнозы не подтвердились, то р=0 и m=0.

Отметим, что сопоставление коэффициентов m для разных моделей может иметь смысл при условии, что доверительные вероятности приняты одинаковыми.