Глава 2. Основные показатели динамики экономических явлений. Использование скользящих средних для сглаживания временных рядов

§ 2.1. Основные показатели динамики экономических явлений

Для количественной оценки динамики явлений применяются статистические показатели: абсолютные приросты, темпы роста, темпы прироста, причем они могут разделяться на цепные, базисные и средние.

В основе расчета этих показателей динамики лежит сравнение уровней временного ряда. Если сравнение осуществляется с одним и тем же уровнем, принятым за базу сравнения, то эти показатели называются базисными. Если сравнение осуществляется при переменной базе, и каждый последующий уровень сравнивается с предыдущим, то вычисленные таким образом показатели называются цепными.

Абсолютный прирост равен разности двух сравниваемых уровней.

Темп роста Т характеризует отношение двух сравниваемых уровней ряда, выраженное в процентах.

Темп прироста К характеризует абсолютный прирост в относительных величинах. Определенный в % темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения. В таблице 2.1. приведены выражения для вычисления базисных и цепных приростов, темпов роста, темпов прироста. При этом использованы следующие обозначения:

Таблица 2.1.

Основные показатели динамики

	Прирост	Темп роста	Темп прироста
Цепной
Базисный
Средний

Для получения обобщающих показателей динамики развития определяются средние величины: средний абсолютный прирост, средний темп роста и прироста.

Описание динамики ряда с помощью среднего прироста соответствует его представлению в виде прямой, проведенной через две крайние точки. В этом случае, чтобы получить прогноз на один шаг вперед, достаточно к последнему наблюдению добавить значение среднего абсолютного прироста.

(2.1.),

где y_n- фактическое значение в последней n- ой точке ряда;

-прогнозная оценка значения уровня в точке n+1;

- значение среднего прироста, рассчитанное для временного ряда .

Очевидно, что такой подход к получению прогнозного значения корректен, если характер развития близок к линейному. На такой равномерный характер развития могут указывать примерно одинаковые значения цепных абсолютных приростов.

Применение среднего темпа роста (и среднего темпа прироста) для описания динамики ряда соответствует его представлению в виде показательной или экспоненциальной кривой, проведенной через две крайние точки. Поэтому использование этого показателя в качестве обобщающего целесообразно для тех процессов, изменение динамики которых происходит примерно с постоянным темпом роста. В этом случае прогнозное значение на i шагов вперед может быть получено по формуле:

(2.2.),

где - прогнозная оценка значения уровня в точке n+i;

- фактическое значение в последней n-ой точке ряда;

- средний темп роста, рассчитанный для ряда (не в % выражении).

К недостаткам среднего прироста и среднего темпа роста следует отнести то, что они учитывают лишь конечный и начальный уровни ряда, исключают влияния промежуточных уровней. Тем не менее, эти показатели имеют весьма широкую область применения, что объясняется чрезвычайной простотой их вычисления. Они могут быть использованы как приближенные, простейшие способы прогнозирования, предшествующие более глубокому количественному и качественному анализу.

§ 2.2. Сглаживание временных рядов с помощью скользящей средней

Распространенным приемом при выявлении тенденции развития является сглаживание временного ряда. Суть различных приемов сглаживания сводится к замене фактических уровней временного ряда расчетными уровнями, которые подвержены колебаниям в меньшей степени. Это способствует более четкому проявлению тенденции развития. Иногда сглаживание применяют как предварительный этап перед использованием других методов выделения тенденции (например, рассматриваемых в третьей главе).

Скользящие средние позволяют сгладить как случайные, так и периодические колебания, выявить имеющуюся тенденцию в развитии процесса, и поэтому, являются важным инструментом при фильтрации компонент временного ряда.

Алгоритм сглаживания по простой скользящей средней может быть представлен в виде следующей последовательности шагов:

1. Определяют длину интервала сглаживания g, включающего в себя g последовательных уровней ряда (g<n). При этом надо иметь в виду, что чем шире интервал сглаживания, тем в большей степени взаимопогашаются колебания, и тенденция развития носит более плавный, сглаженный характер. Чем сильнее колебания, тем шире должен быть интервал сглаживания.

2. Разбивают весь период наблюдений на участки, при этом интервал сглаживания как бы скользит по ряду с шагом, равным 1.

3. Рассчитывают арифметические средние из уровней ряда, образующих каждый участок.

4. Заменяют фактические значения ряда, стоящие в центре каждого участка, на соответствующие средние значения.

При этом удобно брать длину интервала сглаживания g в виде нечетного числа: g=2p+1, т.к. в этом случае полученные значения скользящей средней приходятся на средний член интервала.

Наблюдения, которые берутся для расчета среднего значения, называются активным участком сглаживания.

При нечетном значении g все уровни активного участка могут быть представлены в виде:

а скользящая средняя определена по формуле:

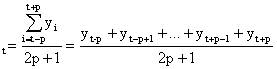(2.3.),

где - фактическое значение i-го уровня;

- значение скользящей средней в момент t;

2p+1- длина интервала сглаживания.

Процедура сглаживания приводит к полному устранению периодических колебаний во временном ряду, если длина интервала сглаживания берется равной или кратной циклу, периоду колебаний.

Для устранения сезонных колебаний желательно было бы использовать четырех- и двенадцатичленную скользящие средние, но при этом не будет выполняться условие нечетности длины интервала сглаживания. Поэтому при четном числе уровней принято первое и последнее наблюдение на активном участке брать с половинными весами:

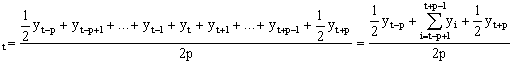(2.4.)

Тогда для сглаживания сезонных колебаний при работе с временными рядами квартальной или месячной динамики можно использовать следующие скользящие средние:

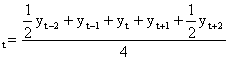(2.5.)

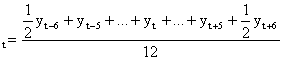(2.6.)

При использовании скользящей средней с длиной активного участка g=2p+1 первые и последние p уровней ряда сгладить нельзя, их значения теряются. Очевидно, что потеря значений последних точек является существенным недостатком, т.к. для исследователя последние "свежие" данные обладают наибольшей информационной ценностью. Рассмотрим один из приемов, позволяющих восстановить потерянные значения временного ряда. Для этого необходимо:

1) Вычислить средний прирост на последнем активном участке

где g- длина активного участка;

- значение последнего уровня на активном участке;

- значение первого уровня на активном участке;

-средний абсолютный прирост.

2) Получить P сглаженных значений в конце временного ряда путем последовательного прибавления среднего абсолютного прироста к последнему сглаженному значению.

Аналогичную процедуру можно реализовать для оценивания первых уровней временного ряда.

Метод простой скользящей средней применим, если графическое изображение динамического ряда напоминает прямую. Когда тренд выравниваемого ряда имеет изгибы, и для исследователя желательно сохранить мелкие волны, применение простой скользящей средней нецелесообразно.

Если для процесса характерно нелинейное развитие, то простая скользящая средняя может привести к существенным искажениям. В этих случаях более надежным является использование взвешенной скользящей средней.

При сглаживании по взвешенной скользящей средней на каждом участке выравнивание осуществляется по полиномам невысоких порядков. Чаще всего используются полиномы 2-го и 3-его порядка. Так как при простой скользящей средней выравнивание на каждом активном участке производится по прямой (полиному первого порядка), то метод простой скользящей средней может рассматриваться как частный случай метода взвешенной скользящей средней. Простая скользящая средняя учитывает все уровни ряда, входящие в активный участок сглаживания, с равными весами, а взвешенная средняя приписывает каждому уровню вес, зависящий от удаления данного уровня до уровня, стоящего в середине активного участка.

Выравнивание с помощью взвешенной скользящей средней осуществляется следующим образом.

Для каждого активного участка подбирается полином вида

параметры которого оцениваются по методу наименьших квадратов. При этом начало отсчета переносится в середину активного участка. Например, для длины интервала сглаживания g=5, индексы уровней активного участка будут следующими i: -2, -1, 0, 1, 2.

Тогда сглаженным значением для уровня, стоящего в середине активного участка, будет значение параметра a₀ подобранного полинома.

Нет необходимости каждый раз заново вычислять весовые коэффициенты при уровнях ряда, входящих в активный участок сглаживания, т.к. они будут одинаковыми для каждого активного участка. Причем при сглаживании по полиному к-ой нечетной степени весовые коэффициенты будут такими же, как при сглаживании по полиному (к-1) степени. В таблице 2.2. представлены весовые коэффициенты при сглаживании по полиному 2-го или 3-го порядка (в зависимости от длины интервала сглаживания).

Так как веса симметричны относительно центрального уровня, то в таблице использована символическая запись: приведены веса для половины уровней активного участка; выделен вес, относящийся к уровню, стоящему в центре участка сглаживания. Для оставшихся уровней веса не приводятся, т. к. они могут быть симметрично отражены.

Например, проиллюстрируем использование таблицы для сглаживания по параболе 2-го порядка по 5-членной взвешенной скользящей средней. Тогда центральное значение на каждом активном участке , будет оцениваться по формуле:

Отметим важные свойства приведенных весов:

1) Они симметричны относительно центрального уровня.

2) Сумма весов с учетом общего множителя, вынесенного за скобки, равна единице.

3) Наличие как положительных, так и отрицательных весов, позволяет сглаженной кривой сохранять различные изгибы кривой тренда.

Существуют приемы, позволяющие с помощью дополнительных вычислений получить сглаженные значения для Р начальных и конечных уровней ряда при длине интервала сглаживания g=2p+1.

Таблица 2.2.

Весовые коэффициенты при сглаживании по полиномам второго и третьего порядка

Длина интервала

Сглаживания

Весовые коэффициенты