Интернет-курс по дисциплине
«Статистика»
Для подготовки бакалавров по направлению «Менеджмент»

Кафедра Бизнес-статистики
Улитина Е.В.
Интернет-курс по дисциплине
«Статистика»
Для подготовки бакалавров по направлению «Менеджмент»
Содержание
Тема 1. Введение в статистику. Предмет, метод и задачи статистики
Вопрос 1. Понятие, предмет и метод статистики.
Вопрос 2. Основные категории статистики.
Вопрос 3. Принципы статистического учета и задачи статистики.
Тема 2. Организация статистического наблюдения
Вопрос 1. Сущность и виды статистического наблюдения.
Вопрос 2. Точность статистического наблюдения.
Тема 3. Сводка и группировка статистических данных. Ряды распределения
Вопрос 1. Статистическая сводка и группировка данных.
Тема 4. Статистические показатели. Абсолютные и относительные показатели.
Вопрос 1. Абсолютные показатели.
Вопрос 2. Относительные показатели.
Тема 5. Статистические показатели. Показатели в форме средних величин
Вопрос 1. Сущность и исходное соотношение средней величины.
Вопрос 2. Средняя арифметическая и ее свойства.
Вопрос 3. Средняя гармоническая, квадратическая и геометрическая.
Вопрос 4. Средняя хронологическая.
Вопрос 5. Структурные средние.
Тема 6. Вариационный анализ финансовых показателей
Вопрос 1. Причины изучения вариации.
Вопрос 2. Показатели вариации и способы их расчета.
Вопрос 3. Математические свойства показателей вариации.
Тема 7. Выборочный метод наблюдения в статистических исследованиях
Вопрос 1. Теоретические основы выборочного наблюдения.
Вопрос 2. Виды выборочного наблюдения. Способы и методы отбора единиц в выборочную совокупность.
Вопрос 3. Средняя и предельная ошибка выборки. Построение доверительных границ для среднего и доли.
Вопрос 4. Определение объема выборочной совокупности.
Тема 8. Анализ взаимосвязи между социально-экономическими явлениями
Вопрос 1. Классификация видов и методов изучения взаимосвязи.
Вопрос 2. Графический метод выявления взаимосвязи.
Вопрос 3. Изучение взаимосвязи между качественными признаками.
Тема 9. Измерение и прогнозирование взаимосвязи с помощью корреляционно-регрессионного анализа
Вопрос 1. Корреляционный анализ.
Вопрос 2. Регрессионный анализ.
Тема 10. Статистический анализ рядов динамики
Вопрос 1. Понятие и классификация рядов динамики.
Вопрос 2. Аналитические показатели динамики.
Вопрос 3. Тенденция ряда динамики и методы ее выявления.
Вопрос 4. Простейшие методы прогнозирования.
Тема 11. Индексный метод анализа социально-экономических явлений
Вопрос 1. Общие понятия об индексах.
Вопрос 2. Индивидуальные индексы.
Вопрос 4. Средние формы сводных индексов.
Вопрос 5. Индексный анализ влияния структурных изменений.
Изучение дисциплины «Статистика» ориентировано на получение студентами знаний статистического анализа различных социально-экономических процессов и явлений. Программа дисциплины «Статистика» разработана с учетом федерального государственного образовательного стандарта по направлению «Менеджмент», утвержденного Министерством образования и науки Российской Федерации.
Дисциплина «Статистика» дает студентам представление о количественных методах изучения социально-экономических процессов, происходящих в современном обществе, расширяет их кругозор.
Владение методами статистики является одним из важнейших деловых качеств менеджера, предпринимателя и экономиста высшей квалификации.
Изучение дисциплины предусматривает лекционные, лабораторные и практические занятия.
Место дисциплины в учебном процессе Университета.
Дисциплина «Статистика» является частью математического и естественнонаучного учебного цикла профессиональной образовательной программы подготовки бакалавров менеджмента и дает основу для дальнейшего изучения других экономических дисциплин, использующих статистические методы.
Цель и задачи дисциплины.
Целью изучения дисциплины является формирование у студентов теоретических знаний о системе статистических показателей, используемых для отражения состояния и развития явлений и процессов общественной жизни, а также практических навыков применения статистических методов для обработки и анализа количественной и качественной информации о развитии социально-экономических процессов и явлений.
Задачи дисциплины:
· изучение методов формирования информационной базы статистики, в т.ч. таких как: статистическое наблюдение, сводка и группировка, абсолютные, относительные и средние величины;
· изучение методов анализа статистических распределений;
· изучение выборочного метода и оценки статистических гипотез;
· изучение индексного метода анализа статистических данных;
· изучение методов исследования динамики и взаимосвязи экономических явлений.
Компетенции, формируемые в результате освоения учебной дисциплины.
В результате освоения дисциплины должны быть сформированы следующие компетенции:
· ОК-15 – овладение методами количественного анализа и моделирования, теоретического и экспериментального исследования;
· ОК-16 – понимание роли и значения информации и информационных технологий в развитии современного общества и экономических знаний;
· ОК-17 – овладение основными методами, способами и средствами получения, хранения, переработки информации, навыками работы с компьютером как средством управления информацией;
· ПК-27 – способность оценивать воздействие макроэкономической среды на функционирование организаций и органов государственного и муниципального управления;
· ПК-31 – умение применять количественные и качественные методы анализа при принятии управленческих решений и строить экономические, финансовые и организационно-управленческие модели;
· ПК-40 – способность анализировать финансовую отчетность и принимать обоснованные инвестиционные, кредитные и финансовые решения;
· ПК-41 – способность оценивать эффективность использования различных систем учета и распределения затрат, иметь навыки калькулирования и анализа себестоимости продукции и способностью принимать обоснованные управленческие решения на основе данных управленческого учета;
· ПК-44 – способность обосновывать решения в сфере управления оборотным капиталом и выбора источника финансирования.
В результате освоения дисциплины студент должен демонстрировать следующие результаты образования:
Знать:
· методы количественного анализа и моделирования (ОК-15);
· роль и значение информации и методы ее получения (ОК-16, ОК-17);
· методы анализа данных, необходимые для решения поставленных экономических задач (ПК-27, ПК-31, ПК-40, ПК-41).
Уметь:
· собирать и обрабатывать данные с помощью различных статистических методов (ОК-17, ПК-31, ПК-40);
· выбирать инструментальные средства для обработки данных в соответствии с поставленной задачей (ОК-16, ОК-17);
· собирать, анализировать и интерпретировать необходимую информацию, содержащуюся в различных формах отчетности и прочих отечественных и зарубежных источниках (ПК-27, ПК-31, ПК-40, ПК-41, ПК-44).
Приобрести навыки:
· сбора и обработки необходимых данных (ОК-16, ОК-17, ПК-40);
· анализа и интерпретации информации, содержащейся в различных отечественных и зарубежных источниках (ПК-27, ПК-31, ПК-40, ПК-41, ПК-44);
· выявления тенденций в развитии социально-экономических процессов (ОК-15).
Формируемые компетенции: ОК-15, ОК-16, ОК-17, ПК-27, ПК-31, ПК-40, ПК-41, ПК-44.
Цель изучения темы состоит в овладении основными дефинициями статистики как науки и принципами организации статистического учета в Российской Федерации.
В результате успешного освоения темы Вы:
Узнаете:
· что такое статистика, что она изучает и какие отрасли статистики существуют;
· важнейшие категории и понятия статистики;
· что такое статистическое исследование и из каких этапов оно состоит.
Приобретете компетенции:
· владение методами теоретического и экспериментального исследования;
· понимание роли и значения информации в развитии современного общества и экономических знаний;
· использование понятия статистики при изучении других дисциплин.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· статистика;
· предмет статистики;
· признак;
· статистическая совокупность;
· единица статистической совокупности;
· вариация;
· статистический показатель.
Вопросы темы:
1. Понятие, предмет и метод статистики.
2. Основные категории статистики.
3. Принципы статистического учета и задачи статистики.
Теоретический материал по теме
Изучаемые статистикой явления и процессы многообразны. В первую очередь, статистика изучает все, что связано с экономической деятельностью общества: производство и реализацию промышленной и сельскохозяйственной продукции, строительство и реконструкцию основных фондов, работу транспорта и связи, формирование и движение финансовых потоков. Статистические методы широко используются в анализе социальных процессов и явлений – занятости и безработицы, доходов населения, изучении общественного мнения и т.д. Большую роль играет статистика в технике и производственной деятельности, например, в организации контроля качества продукции. Методы статистики применяются в бухгалтерском учете, экономическом анализе, менеджменте, маркетинге, логистике, страховании и оценочной деятельности, в других научных и практических областях.
Первоначально статистику определяли как «государствоведение», поскольку в основном она занималась описанием особенностей государств и служила для учета населения, сельскохозяйственных средств производства, для повышения эффективности взимания налогов и сборов, т.е. для реализации фискальных целей государства. С развитием торговли и международных товарно-денежных отношений описательной функции статистики становится недостаточно, что послужило стимулом для выделения ее в самостоятельную науку.
В настоящее время под термином «статистика» чаще всего понимается следующее.
Статистика – это искусство и наука сбора и анализа данных.
Поскольку данными называется любой вид зарегистрированной информации, статистика играет важную роль во всех сферах деятельности человека. Известный английский статистик У.Дж. Рейхман еще в начале прошлого века заметил: «Едва ли не в каждом своем аспекте явления природы, а также человеческая и прочая деятельности поддаются сейчас измерению при помощи статистических показателей».
Статистика – это одна из форм практической деятельности человека, цель которой – сбор, обработка и анализ данных о различных социальных, общественных и экономических явлениях.
Исторически данную функцию статистики реализует государство. Во всех странах мира деятельностью по сбору и обобщению информации для внутренних и внешних потребностей экономики занимаются специально учреждаемые государствами органы – статистические комитеты и комиссии, статистические бюро. В нашем государстве эта работа выполняется Федеральной службой государственной статистики (Росстат) (прежнее название организации – Государственный комитет РФ по статистике). В задачу таких государственных и ведомственных органов входят сбор, обобщение и публикация статистических данных в целом по стране, например, в России издается Статистический ежегодник «Россия в цифрах», а также по отдельным регионам и отраслям экономики.
Статистикой называют также числовые (цифровые) или количественные данные, характеризующие различные объекты и явления.
Но, прежде всего, статистика – это самостоятельная общественная наука, которая имеет свой предмет и специфические методы исследования.
Статистика – это наука, которая изучает количественную сторону массовых социально-экономических явлений и процессов в неразрывной связи с их качественной стороной, выявляет основные характеристики и закономерности развития этих явлений и процессов в конкретных условиях места и времени.
Из данного определения следуют основные особенности предмета статистики и статистики как науки.
Предметом статистики является количественная сторона массовых качественно определенных социально-экономических явлений и процессов, отображаемых посредством статистически показателей.
Каковы же особенности статистики как науки?
1. В отличие от других общественных наук статистика изучает количественную сторону общественных явлений.
То есть статистика выявляет основные характеристики различных явлений общества и экономики, характеризует их, сравнивает между собой, анализирует происходящие с этими явлениями изменения, используя числа, т.е. количественные показатели.
2. Статистика изучает массовые явления и выявляет основные закономерности их развития.
Очевидно, что для установления закономерности развития процесса в целом необходимо проанализировать множество единичных случаев. Например, выявить, какая из двух групп колледжа лучше успевает в обучении, невозможно, если взять по одному студенту из этих групп и сравнить полученные ими оценки. Для ответа на этот вопрос следует обобщить экзаменационные оценки всех студентов в каждой группе и сравнить полученные результаты. Поэтому статистика изучает не единичные факты, а массовые социально-экономические явления. При этом отдельные факты не игнорируются, а рассматриваются как составляющие общего явления. Например, изучая продолжительность жизни населения и смертность, статистика использует данные о количестве умерших и регистрирует, в каком возрасте произошла смерть. Но установлением причины смерти занимается другая наука – медицина.
3. Для статистики исключительно важна качественная определенность используемых числовых данных.
Например, для математики действие 20 + 15 = 35 уже является результатом. А статистик, прежде чем суммировать числа 20 и 15, обязательно бы выяснил, что они характеризуют и в каких единицах измерения они выражены. Ведь если числа 20 и 15 имеют разную природу, единицы измерения их просто нельзя суммировать, хотя арифметически, без учета их качественного содержания, это возможно.
Статистика изучает различные аспекты жизни общества. В зависимости от специфики объекта исследования различают отдельные отрасли статистики (рис. 1).

Рис. 1. Отрасли статистики
Теория статистики рассматривает общие понятия и методы сбора, обработки и анализа данных, разрабатывает общие показатели и методы изучения структуры, взаимосвязи и динамики социально-экономических процессов и явлений. Разрабатываемые ей методы и показатели используются другими отраслевыми статистиками.
Экономическая статистика изучает количественные закономерности происходящих в экономике явлений и процессов, выявляет основные тенденции экономического развития и их воздействие на уровень жизни населения на макроуровне, т.е. на уровне крупного региона или страны в целом. К основным показателям экономической статистики относятся: валовой внутренний продукт; валовой региональный продукт; такие элементы национального богатства, как основные фонды, материальные и оборотные средства, имущество домашних хозяйств.
Отраслевые статистики изучают основные показатели, закономерности и тенденции развития отраслей экономики.
Статистика населения изучает численный и национальный состав, а также возрастно-половую структуру населения, его размещение и воспроизводство как по стране в целом, так и в разрезе территориальных единиц. Одной из основных задач статистики населения является построение краткосрочных и долгосрочных демографических прогнозов.
Социальная статистика изучает социальную структуру населения, его уровень жизни и, в частности, доходы, уровень образования и культуры, состояние здоровья и медицинского обслуживания, использование свободного времени, общественное мнение, уровень преступности и другие социальные аспекты жизнедеятельности общества.
Для того чтобы получить общее представление о статистической методологии, необходимо рассмотреть сам процесс статистического исследования, который включает четыре основных этапа.
1 этап. Сбор первичного статистического материала, проверка его полноты и достоверности. С этой целью применяются специальные методы статистического наблюдения. От качества полученных исходных данных во многом зависят окончательные результаты всего исследования.
2 этап. Предварительная обработка данных. Собранную информацию необходимо упорядочить, систематизировать, т.е. подготовить для дальнейшей работы. Основной метод, используемый на данном этапе – метод группировок. В результате его реализации от больших массивов данных исследователь переходит к компактным и удобным для анализа статистическим таблицам.
3 этап. Расчет и интерпретация обобщающих статистических показателей. На данном этапе рассчитываются показатели среднего уровня и вариации, структуры, взаимосвязи и динамики изучаемых процессов и явлений. Полученные результаты анализируются и формулируются выводы.
4 этап. Моделирование взаимосвязей между социально-экономическими процессами и явлениями.
Используемые в процессе реализации всех этапов статистические приемы и методы в целом составляют методологию статистики.
Как любая наука, статистика имеет свои специальные термины-категории, которые находятся в постоянном обиходе и используются при объяснении других понятий и методов. К важнейшим категориям статистики относятся: признак; статистическая совокупность, единица статистической совокупности, вариация, статистический показатель.
Признак – это объективная характеристика какого-либо объекта или явления, характерная черта или свойство, которое может быть определено или измерено. Именно значения различных признаков наблюдаются и регистрируются на первом этапе исследования – наблюдении.
Например, признаками, характеризующими промышленное предприятие, являются выручка от реализации продукции, прибыль, стоимость основных фондов, численность персонала и др. Признаками человека являются возраст, пол, место жительства, профессия, доход.
Значение, которое может принимать признак, называется вариантом. Например, существуют всего четыре варианта значений признака «экзаменационная оценка»: «2», «3», «4», «5». Если же учитывать оценки, проставляемые в зачетную книжку, то таких вариантов остается три, так как оценка «2» в зачетку не проставляется. У отдельно взятого учащегося в зачетке может быть указано множество оценок по разным предметам, но вариантов будет по-прежнему три, а возможно, два или один, если студент учится без троек и четверок. Признаки подразделяются на количественные и качественные (рис. 2).

Рис. 2. Классификация видов признаков
Количественным является признак, отдельные варианты которого имеют числовое выражение и отражают размеры, масштабы изучаемого объекта или явления. К количественным признакам, например, относятся доход домохозяйства, площадь жилого помещения, цена товара, стаж работы. Количественные признаки в статистике преобладают над другими видами признаков, они наиболее информативны, аналитичны, именно на их использование нацелена большая часть статистического инструментария.
Непрерывные количественные признаки могут принимать любые числовые значения; например, прибыль предприятия может быть и положительной, причем от одного рубля до триллионов рублей, и нулевой, и даже отрицательной, если предприятие терпит убытки.
Дискретные количественные признаки принимают значения, ограниченные определенным диапазоном, широта которого зависит от особенностей признака. Например, при изучении семей по числу детей типичными вариантами признака будут 0, 1, 2 и 3, хотя есть семьи, в которых растут и воспитываются и 4, и 5 и даже большее количество детей.
Качественные признаки, в отличие от количественных, не поддаются прямому числовому описанию. Они характеризуют различные свойства объектов и явлений, отражают их состояние или отдельные характеристики. Например, к качественным признакам относятся форма собственности предприятия, пол человека, уровень образования, квалификация специалиста.
Качественный признак называется альтернативным, если он имеет только два варианта значений. Например, пол человека может быть мужским или женским, население страны или региона обычно делится на городское и сельское. Альтернативный признак может иметь и числовое выражение. Например, семья может иметь доход в размере «до 15 тыс. руб. в месяц» и «15 тыс. руб. в месяц и более».
В отличие от альтернативного атрибутивный признак имеет более двух вариантов, которые выражаются в виде понятий или наименований. Например, район проживания, вид продукции, специальность работника, цвет товара. Такие признаки имеют место в различных областях исследования, но чаще с ними работают маркетологи, социологи и психологи.
Порядковые признаки отличаются от атрибутивных тем, что они имеют несколько ранжированных, т.е. упорядоченных по возрастанию или убыванию, качественных вариантов. Например, уровень образования (начальное, общее среднее и т.д.), уровень квалификации, воинское звание. Отдельные варианты порядкового признака трудно соизмерить количественно. Например, понятно, что образованность человека с высшим образованием выше, чем со средним специальным, но при этом нельзя утверждать, что она выше на 20 % или на 30 %. Водительская категория «Е» выше, чем категория «В», но количественных пропорций между ними не существует. Порядковый признак может иметь числовое выражение. Например, тарифный разряд рабочего или служащего, рейтинговые и экзаменационные оценки. Однако варианты таких признаков также не имеют количественных пропорций: рабочий 6-го разряда не обязательно в два раза больше вырабатывает продукции и в два раза больше зарабатывает, чем рабочий 3-го разряда.
Статистика изучает социально-экономические явления комплексно, поэтому, приступая к исследованию, отдельные объекты или явления объединяются по их качественному содержанию в специальные группы.
Статистическая совокупность – это реально существующее множество объектов или явлений, объединенных хотя бы одним общим признаком и обладающих внутренней взаимосвязью и целостностью.
Статистика имеет дело с совокупностями промышленных, сельскохозяйственных, строительных и торговых предприятий, с совокупностью коммерческих банков, с совокупностью населения страны или отдельного ее региона. Так, например, всех жителей г. Москвы можно рассматривать как статистическую совокупность, так как один признак – город проживания – будет у всех одинаковым. Индивидуальный объект или явление, составляющее статистическую совокупность, называется единицей статистической совокупности.
При проведении исследования именно у единиц совокупности измеряются или фиксируются важные для исследования признаки. Для отрасли единицей совокупности будет являться отдельное предприятие, для банковской системы – отдельный банк. В некоторых случаях для одной и той же совокупности можно выделить разные группы единиц. Например, при изучении половозрастной структуры населения единицей является отдельный человек, при изучении доходов, обеспеченности жильем и предметами длительного пользования (телевизоры, холодильники и т.п.) единицей будет являться семья или домохозяйство.
Общее число единиц, образующих статистическую совокупность, называется объемом совокупности.
Объем совокупности следует отличать от объема признака, т.е. суммарного значения признака по всем единицам изучаемой совокупности. Так, число предприятий в отрасли – это объем совокупности, а общий выпуск продукции всеми предприятиями отрасли – объем признака.
Одной из важнейших характеристик статистической совокупности является ее однородность. Однородной является совокупность, единицы которой близки между собой по значениям признаков, существенных для данного исследования. Многие методы и приемы статистического исследования применимы лишь к однородным совокупностям.
Внутри статистической совокупности отдельные объекты и явления могут сильно отличаться друг от друга по своим свойствам и характеристикам. Например, у единиц совокупности «Население г. Москвы» кроме общего города проживания есть множество признаков, по которым единицы совокупности – москвичи – отличаются друг от друга: возраст, уровень образования, размер дохода. На языке статистики этот пример звучит так: население Москвы варьирует по возрасту, уровню образования, доходу. Или: внутри совокупности «население г. Москвы» существует вариация признаков «возраст», «уровень образования» и «доход».
Вариация – это изменяемость, колеблемость величины признака у различных единиц совокупности, т.е. принятие единицами совокупности разных вариантов значений признака.
Что является причиной такой изменчивости?
Во-первых, индивидуальные особенности изучаемых объектов. Например: коммерческие банки варьируют по величине активов в зависимости от размера уставного фонда и реализуемой финансовой политики; работники предприятия имеют разную производительность труда в зависимости от их квалификации и мотивации, но также на производительность труда влияют состояние здоровья, настроение работника и общая атмосфера в трудовом коллективе.
Во-вторых, изменяемость происходит под воздействием определенных условий, в том числе и непредвиденных (форс-мажорных). Например, вариация городов по численности населения зависит от географического положения города, развитости городской инфраструктуры и экономического положения в регионе. Спрос на туристические поездки в Таиланд в начале 2005 года значительно снизился после разрушений, вызванных серией цунами, что отразилось на выручке туристических операторов, организующих отдых в этой стране.
Именно наличие вариации и изменчивости данных определяет необходимость статистики как науки и делает неизбежным процесс постоянного отслеживания и анализа информации о том, как развивается общество и экономика, как работает та или иная отрасль, насколько эффективно функционирует конкретное предприятие.
Важную роль в статистике играет закон больших чисел – общий принцип, в силу которого количественные закономерности, присущие массовым явлениям, отчетливо проявляются лишь при достаточно большом числе наблюдений. Единичные явления в большей степени подвержены действию случайных и несущественных факторов, чем масса в целом. При большом числе наблюдений случайные отклонения от общей закономерности развития взаимно погашаются. В результате этого обобщающие показатели становятся типичными, отражающими действие только постоянных и существенных факторов.
Статистическое исследование всегда завершается расчетом и анализом различных по виду и форме выражения статистических показателей.
Статистический показатель представляет собой количественную характеристику социально-экономических явлений и процессов в конкретных условиях места и времени.
Статистический показатель непосредственно связан с внутренним содержанием изучаемого явления или процесса, его сущностью. Изучаемые статистикой процессы и явления достаточно сложны и не могут быть описаны одним отдельно взятым показателем. В таких случаях используется система статистических показателей, позволяющих учесть различные характеристики изучаемого объекта или явления. Так, например, изучая промышленное предприятие, нельзя ограничиться только величиной выпуска продукции. Для полной экономической характеристики необходимо учесть численность персонала, производительность его труда, стоимость основных производственных фондов, финансовые показатели – затраты, прибыль, инвестиции в развитие производства.
В отличие от признака статистический показатель получается расчетным путем. Это может быть простой подсчет единиц совокупности, суммирование значений признака части или всех единиц совокупности, сравнение двух или нескольких величин, а также более сложные расчеты.
Все показатели можно классифицировать по охвату единиц совокупности, временной и пространственной определенности (рис. 3).

Рис. 3. Классификация статистических показателей
В Российской Федерации основные вопросы организации статистического учета регулируются Федеральным законом от 29 ноября 2007 г. № 282-ФЗ «Об официальном статистическом учете и системе государственной статистики в Российской Федерации» (с изменениями и дополнениями от 19 октября 2011 г., 16 октября 2012 г., 2 июля 2013 г.).
Основные задачи статистики на уровне государства состоят в обеспечении принципов официального статистического учета и системы государственной статистики, изложенных в Статье 4 ФЗ № 282.
Принципами официального статистического учета и системы государственной статистики являются:
6) согласованность действий субъектов официального статистического учета;
Федеральным органом исполнительной власти, осуществляющим функции по выработке государственной политики и нормативно-правовому регулированию в сфере официального статистического учета, формированию официальной статистической информации о социальных, экономических, демографических, экологических и других общественных процессах в Российской Федерации, а также в порядке и случаях, установленных законодательством Российской Федерации, по контролю в сфере официального статистического учета является Федеральная служба государственной статистики (Росстат).
1. Какие значения имеет термин «статистика»?
2. В чем особенности статистики как науки?
3. Какие существуют отрасли статистики?
4. Что является объектом статистики как науки?
5. Каковы основные категории статистики?
6. Сколько этапов можно выделить в статистическом исследовании?
7. Каким законом регулируются вопросы статистического учета в Российской Федерации? Сколько принципов официального статистического учета сформулировано в этом законе?
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Методологические положения по статистике. – М.: Госкомстат России, 2010.
2. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
Нормативно-правовые акты:
1. Федеральный закон от 29 ноября 2007 г. № 282-ФЗ «Об официальном статистическом учете и системе государственной статистики в Российской Федерации».
Задание 1.
Укажите, к каким видам – количественным или качественным – относятся указанные ниже признаки:
|
Признак |
Вид признака |
|
1. Среднесписочная численность работников предприятия. |
|
|
2. Уровень образования сотрудника. |
|
|
3. Чистая прибыль предприятия. |
|
|
4. Форма собственности предприятия. |
|
|
5. Товарооборота торгового предприятия за месяц. |
|
Задание 2.
Укажите единицу каждой приведенной ниже совокупности:
|
Совокупность |
Единица совокупности |
|
1. Население г. Москвы. |
|
|
2. Торговая сеть универсамов «Пятерочка». |
|
|
3. Совокупность коммерческих банков, обслуживающих юридических лиц с численностью персонала до 100 человек. |
|
|
4. Персонал корпорации ОАО «Газпром». |
|
Цель изучения темы состоит в формировании системы знаний и компетенций о формах и видах получения информации в ходе подготовки и проведения статистического наблюдения.
В результате успешного освоения темы Вы:
Узнаете:
· что такое статистическое наблюдение;
· какие формы наблюдения существуют;
· что такое перепись населения и для чего она проводится.
Приобретете компетенции:
· владение методами теоретического и экспериментального исследования;
· понимание роли и значения информации в развитии современного общества и экономических знаний;
· владение основными методами, способами и средствами получения, хранения, переработки информации;
· умение различать и выбирать вид наблюдения для сбора данных.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· статистическое наблюдение;
· план статистического наблюдения;
· статистическая отчетность;
· специально организованное наблюдение;
· перепись;
· регистровое наблюдение;
· сплошное и несплошное наблюдение;
· непрерывное и прерывное наблюдение;
· непосредственное и документальное наблюдение, опрос;
· ошибки регистрации, ошибки репрезентативности;
· логический контроль, арифметический контроль.
Вопросы темы:
1. Сущность и виды статистического наблюдения.
2. Точность статистического наблюдения.
Теоретический материал по теме
Статистическое наблюдение – это массовый, планомерный, научно организованный сбор данных о социально-экономических явлениях и процессах, заключающийся в регистрации отобранных признаков у каждой единицы изучаемой совокупности. Например, при переписи населения по каждому жителю страны регистрируются сведения о поле, возрасте, семейном положении, образовании и др.
Статистическое наблюдение, как правило, носит массовый характер – для получения наиболее точных данных и выявления закономерностей и взаимосвязей при проведении наблюдения необходимо получить данные от максимально возможного числа изучаемых единиц совокупности.
Любое исследование проводится по заранее разработанному плану. Структура элементов плана статистического наблюдения представлена на рис. 4.

Рис. 4. Содержание плана статистического наблюдения
Основная цель статистического наблюдения – это сбор статистической информации о социально-экономических явлениях и процессах для получения обобщающих характеристик.
Различают три основные формы статистического наблюдения (рис. 5).
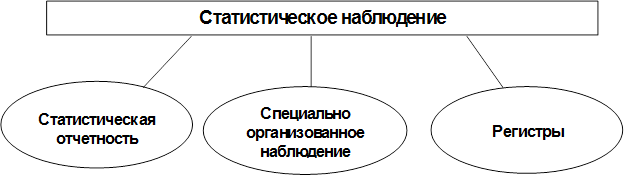
Рис. 5. Формы статистического наблюдения
Статистическая отчетность – это способ получения статистической информации от юридических лиц. Отчетность представляет собой специально разработанные формы, включающие в себя те признаки, которые подлежат регистрации. Формы статистической отчетности разрабатываются и утверждаются органами государственной статистики РФ. Любое юридическое лицо, являющееся субъектом экономики РФ, обязано предоставлять отчетность органам государственной статистики по месту своей регистрации по установленным отчетным формам и в установленные сроки.
Специально организованные статистические наблюдения проводятся для получения данных, не содержащихся в предоставляемой отчетности или необходимых для проверки или уточнения данных, содержащихся в отчетах. Особым их видом является перепись.
Перепись – это специально проводимые широкомасштабные работы по сбору необходимой статистической информации об изучаемых объектах в границах отрасли, региона или страны в целом.
Перепись населения – это организация сбора, обработки и публикации демографических, экономических и социальных данных обо всем населении, проживающем в определенный момент времени в стране.
Принципы переписи населения: всеобщность охвата населения переписью; непосредственное получение сведений путем опроса конкретных людей; самоопределение людей при ответах на вопросы (без предъявления подтверждающих сведения документов); конфиденциальность сообщаемых населением сведений (результаты переписи публикуются только в сводном виде по стране, краю, области).
В 2006 году по состоянию на 1 июля проводилась Всероссийская сельскохозяйственная перепись – массовый сбор данных от юридических и физических лиц, которые имеют земельные участки, предназначенные или используемые для производства сельскохозяйственной продукции, либо имеют сельскохозяйственных животных. Результаты этой переписи имели важное значение для разработки эффективной агропромышленной политики и формирования объективной информации о состоянии продовольственного комплекса, который влияет на продовольственную и экономическую безопасность страны.
Органами статистики проводятся также переписи многолетних насаждений, жилого фонда, незавершенного строительства и пр.
Кроме переписей, к специально организованному наблюдению относятся другие единовременные работы по сбору информации, в частности в рамках социологических или маркетинговых исследований.
Регистровое наблюдение представляет собой постоянный мониторинг состояния и развития наблюдаемых единиц, заключающийся в размещении и своевременной актуализации информации о них в базе данных. В статистической практике ряда стран применяют регистры населения, постоянно актуализируемые списки жителей страны с указанием их основных социально-демографических признаков, и регистры предприятий.
Регистры предприятий содержат данные о времени создания (регистрации) предприятия, его названии и адресе, об организационно-правовой форме, структуре, виде экономической деятельности, количестве занятых, основных экономических показателях из данных бухгалтерской отчетности и др. В России таким регистром является Статистический регистр хозяйствующих субъектов – база данных об организациях, созданных на территории РФ, их местных единицах, индивидуальных предпринимателях и других типах хозяйствующих субъектов. Статистический регистр ведет Федеральная служба государственной статистики.
Классификация видов наблюдения представлена на рис. 6.
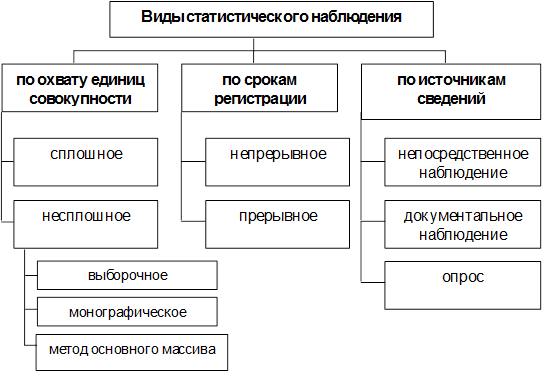
Рис. 6. Виды статистического наблюдения
По охвату единиц совокупности наблюдение бывает двух видов: сплошное и несплошное. При сплошном наблюдении обследованию подвергаются все единицы изучаемой совокупности. Примером сплошного наблюдения могут служить переписи населения.
При несплошном наблюдении обследованию подвергается только часть единиц изучаемой совокупности. Различают следующие виды несплошного наблюдения: выборочное наблюдение, монографическое обследование, метод основного массива.
Выборочным называют наблюдение, основанное на принципе случайного отбора тех единиц изучаемой совокупности, которые должны быть подвергнуты наблюдению. Выборочное наблюдение, при правильной его организации и проведении, дает достаточно достоверные данные для характеристики изучаемой совокупности в целом. Во многих случаях им вполне можно заменить сплошной учет. При этом обеспечивается значительная экономия средств, затрачиваемых на сбор и обработку данных.
Монографическое обследование представляет собой детальное, глубокое изучение и описание отдельных единиц совокупности. Такое исследование проводится с целью выявления имеющихся резервов, оценки результатов экономических экспериментов.
Метод основного массива заключается в том, что обследованию подвергаются наиболее крупные единицы, которые имеют преобладающий удельный вес в совокупности по основному для данного исследования признаку. Например, в ряде отраслей подавляющий объем выпуска продукции приходится на крупные и средние предприятия, поэтому результаты деятельности малых предприятий в этих отраслях практически не отражаются на обобщающих статистических показателях.
По срокам регистрации наблюдение может быть непрерывным (текущим) и прерывным. Непрерывным называют наблюдение, которое ведется постоянно, и регистрация фактов производится по мере их свершения. Так, например, осуществляется регистрация рождений, заключенных браков, разводов и др. в органах ЗАГС.
Прерывное наблюдение повторяется через определенные равные промежутки времени (например, ежегодное предоставление отчетности в органы государственной статистики) или по мере необходимости, без соблюдения строгой периодичности (как, например, перепись многолетних насаждений, проведенная один раз в прошлом веке).
По источнику сведений различают непосредственное наблюдение, документальное наблюдение и опрос.
Непосредственным называют такое наблюдение, при котором сами регистраторы путем непосредственного замера, взвешивания или подсчета устанавливают значение признака и производят запись в формуляре наблюдения. Пример: инвентаризация основных средств на предприятиях.
Документальное наблюдение предполагает запись ответов на вопросы формуляра на основании соответствующих документов. Например: сбор данных об успеваемости студентов вуза на основе зачетно-экзаменационных ведомостей, заполнение форм статистической отчетности на основании данных бухгалтерского учета и т.п.
Опрос – это наблюдение, при котором ответы на вопросы формуляра записываются со слов опрашиваемого (респондента). Этим способом проводятся переписи населения, опросы общественного мнения.
В статистике применяются следующие способы сбора сведений: отчетный, экспедиционный, самоисчисление, анкетный.
Отчетный способ заключается в обязательном представлении хозяйствующими субъектами статистических отчетов о своей деятельности в установленной форме и в установленные сроки.
Экспедиционный способ наблюдения заключается в том, что специально привлеченные и обученные работники посещают каждую единицу наблюдения и сами заполняют формуляр наблюдения. Этим способом собираются сведения при переписях населения.
При способе самоисчисления формуляры заполняют сами опрашиваемые. Обязанность специально привлеченных для получения информации сотрудников состоит в раздаче формуляров, инструктаже опрашиваемых, сборе и проверке правильности заполнения формуляров.
Анкетный способ – это сбор данных с помощью специальных вопросников, рассылаемых определенному кругу лиц или публикуемых в периодической печати. Как правило, этим способом получения информации пользуются при проведении социологических опросов. Также многие крупные производители бытовой техники, мебели и других предметов потребления вкладывают анкеты в упаковку товара с просьбой заполнить и вернуть их производителю по указанному адресу.
Под точностью в статистике понимают степень соответствия данных наблюдения реальным их значениям. Возникающие расхождения называются ошибками. Ошибки определяются как разность или как отношение между этими значениями. Как правило, ошибки возникают при регистрации сведений или при измерении.
Ошибки регистрации возникают вследствие неправильного установления фактов в процессе наблюдения, или ошибочной их записи, или того и другого вместе. Случайные ошибки возникают в результате опечаток, описок, оговорок. Например, при регистрации даты регистратор вместо 15 июня указал 15 июля. При большом числе наблюдений благодаря действию закона больших чисел эти ошибки более или менее взаимно погашаются.
Систематические ошибки наиболее опасны, поскольку приводят к сильному искажению данных. Наиболее показательными такими ошибками являются: занижение или округление населением своего возраста на цифры, оканчивающиеся на 5 или 0; сокрытие экономическими субъектами реальных размеров финансовых результатов их деятельности, стремление респондентов указать заниженное значение своего дохода и т.п.
При несплошном наблюдении возникают ошибки репрезентативности (или ошибки представительности). Они заключаются в том, что значения признаков по отобранной выборочной совокупности не отражают реально существующей картины в совокупности в целом.
С целью выявления ошибок проводится контроль полученных материалов. После проведения наблюдения весь собранный материал проверяют на полноту охвата единиц. Если выявлены упущенные единицы наблюдения, дальнейшие действия зависят от того, представляется возможным восполнение пробелов или нет.
Для проверки качества заполнения формуляров и других документов наблюдения используют логический и арифметический контроль.
Логический контроль состоит в сопоставлении между собой ответов на вопросы формуляра наблюдения и выяснении их логической совместимости. При обнаружении несовместимых ответов пытаются путем дальнейших сопоставлений установить, какой из ответов является верным.
Арифметический контроль состоит в проверке различных расчетов, результаты которых проведены в формуляре наблюдения, в частности: итогов, вычисления процентов, расчетов средних величин и т.п.
1. Что такое перепись населения и почему необходимо ее проводить?
2. Для чего формируются регистры предприятий?
3. К какому виду наблюдения относится регистрация факта смерти или рождения человека?
4. Почему все зарегистрированные хозяйствующие субъекты обязаны предоставлять статистическую отчетность в органы статистики?
5. В чем преимущества и недостатки сплошного и несплошного методов наблюдения?
6. В чем заключаются ошибки регистрации?
7. В каких случаях говорят о наличии ошибок репрезентативности?
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: учебник / Под ред. чл.-корр. РАН И.И. Елисеевой. – М.: Финансы и статистика, 2004.
2. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Интернет-ресурсы:
1. Формы федерального статистического наблюдения. – http://www.gks.ru/metod/forma.html
Задание 1.
Внимательно изучив копии формуляра Всероссийской переписи населения 2002 г. (рис. 7, 8) и 2010 г. (рис. 9, 10), выпишите попарно номера вопросов переписи 2002 г., идентичных (абсолютно совпадающих) по формулировкам вопросам переписи 2010 г. (например: № 2 (2002 г.) – № 2 (2010 г.)).
Задание 2.
Внимательно изучив копии формуляра Всероссийской переписи населения 2002 г. (рис. 7, 8) и 2010 г. (рис. 9, 10), выпишите номера вопросов переписи 2010 г., которых не было в бланках переписи 2002 г.
Задание 3.
С помощью логического контроля проведите проверку приведенных ниже ответов на вопросы переписного листа переписи населения. Отметьте вопросы, в ответах на которые вероятнее всего произведены ошибочные записи:
1. Фамилия, имя, отчество: Иванова Ирина Петровна.
2. Пол: мужской.
3. Возраст: 5 лет.
4. Состоит ли в браке в настоящее время: да.
5. Национальность: русская.
6. Родной язык: русский.
7. Образование: начальное среднее.
8. Место работы: детский сад.
9. Занятие по этому месту работы: медицинская сестра.

Рис. 7. Копия формуляра Всероссийской переписи населения 2002 г. (Д1, лицевая сторона)

Рис. 8. Копия формуляра Всероссийской переписи населения 2002 г. (Д2, оборотная сторона)

Рис. 9. Копия формуляра Всероссийской переписи населения 2010 г. (Лист Л1)

Рис. 10. Копия формуляра Всероссийской переписи населения 2010 г. (Лист Л2)
Ответы к заданиям:
Задание 1. 2(2002) – 2(2010); 3(2002) – 3(2010); 4(2002) – 5(2010); 5(2002) – 4(2010); 6(2002) – 6(2010); 7(2002) – 7(2010); 9.1(2002) – 9.1(2010); 9.2(2002) – 9.2.(2010); 10(2002) – 10(2010); 11.1(2002) – 11.2.(2010); 11.4(2002) – 11.3(2010); 11.6(2002) – 11.5(2010); 13(2002) – 13.1(2010).
Задание 2. 8.2; 9.3; 10.2; 11.4.
Задание 3. 2, 3, 7.
Цель изучения темы состоит в формировании системы знаний и компетенций о методах сбора и систематизации статистической информации, в частности о формах и видах статистической сводки и группировки данных, методике построения группировок, построении и графическом представлении рядов распределения.
В результате успешного освоения темы Вы:
Узнаете:
· что такое сводка и группировка данных;
· какие виды группировок существуют и для чего они применяются;
· как определить, сколько групп можно выделить внутри любой статистической совокупности;
· как оформляются результаты группировки данных;
· что такое ряд распределения и чем он отличается от группировки;
· каким образом можно наглядно представить ряд распределения;
· что такое полигон и гистограмма распределения.
Приобретете компетенции:
· владение методами теоретического и экспериментального исследования;
· понимание роли и значения информации в развитии современного общества и экономических знаний;
· владение основными методами, способами и средствами получения, хранения, переработки информации;
· способность оценивать воздействие макроэкономической среды на функционирование организаций;
· способность анализировать финансовую отчетность и принимать обоснованные решения;
· владение методами построения и анализа статистических группировок по любому набору первичных статистических данных.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· сводка;
· группировка и ее виды;
· группировочный признак;
· интервал, границы интервала, ширина интервала;
· ряд распределения, атрибутивные и вариационные ряды;
· частоты, частости;
· полигон распределения;
· гистограмма распределения;
· плотность распределения.
Вопросы темы:
1. Статистическая сводка и группировка данных.
2. Ряды распределения.
Теоретический материал по теме
Собранные данные необходимо систематизировать и подготовить к последующей обработке. Для упорядочивания исходных данных статистика применяет два основных метода – метод сводки и метод группировки.
Сводка – это научная обработка первичных данных с целью получения обобщенных характеристик изучаемого социально-экономического явления по ряду существенных для него признаков (рис. 11).
По глубине и точности обработки данных различают простую и сложную сводку. Данные можно обрабатывать централизовано – в одной организации или децентрализовано – последовательно передавая результаты сводки от территориальных органов в федеральные (как при обработке отчетности).
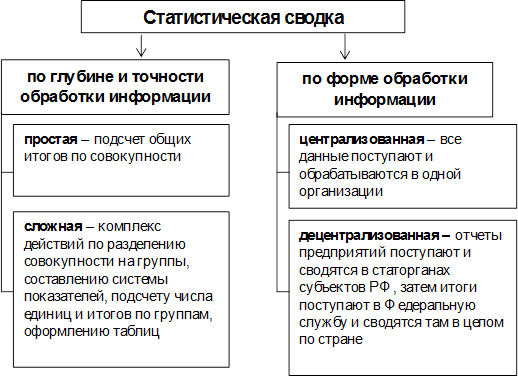
Рис. 11. Виды статистических сводок
Группировкой называется разбиение общей совокупности единиц объекта наблюдения по одному или нескольким существенным признакам на более однородные группы. Группы могут различаться между собой по числу объектов и в качественном отношении.
В соответствии с познавательными задачами различают три основных вида группировок (рис. 12).

Рис. 12. Виды группировок
Типологическая группировка – это разбиение разнородной совокупности единиц наблюдения на отдельные качественно однородные группы и выявление на их основе устойчивых социально-экономических типов явлений. Например: группировка предприятий и организаций по формам собственности; группировка торговых предприятий по их принадлежности к сферам промышленных и продовольственных товаров.
Структурная группировка предназначена для изучения состава совокупности по какому-либо признаку. Например: изучение возрастной структуры безработных в Российской Федерации (табл. 1).
Таблица 1.
Распределение численности безработных по возрастным группам и средний возраст безработных в 2011 г.
(в среднем за год; в процентах к итогу)
|
|
Всего |
Мужчины |
Женщины |
|
Безработные, всего |
100 |
100 |
100 |
|
в том числе в возрасте, лет: |
|
|
|
|
до 20 |
5,7 |
5,9 |
5,6 |
|
20–24 |
20,9 |
21,5 |
20,2 |
|
25–29 |
15,5 |
15,2 |
15,8 |
|
30–34 |
11,7 |
11,8 |
11,6 |
|
35–39 |
9,6 |
9,5 |
9,7 |
|
40–44 |
8,1 |
8,1 |
8,2 |
|
45–49 |
10,3 |
9,7 |
11,0 |
|
50–54 |
10,3 |
9,5 |
11,2 |
|
55–59 |
5,7 |
6,6 |
4,6 |
|
60–72 |
2,2 |
2,1 |
2,3 |
|
Сpедний возpаст безработных, лет |
35,3 |
35,1 |
35,4 |
Аналитическая группировка выявляет взаимосвязи между изучаемыми признаками. В статистике выделяют факторные и результативные признаки. Факторными называются признаки, под воздействием которых изменяются другие, результативные признаки. Взаимосвязь проявляется в том, что с возрастанием или убыванием значения факторного признака систематически возрастает или убывает значение признака результативного, и наоборот.
При построении аналитической группировки, как правило, единицы совокупности группируются по факторному признаку; каждая выделенная группа характеризуется средними величинами результативного признака. Пример аналитической группировки представлен в табл. 2.
Таблица 2.
Группировка зависимости суммы кредитов, выданных коммерческими банками, от размера процентной ставки
|
№ п/п |
Группы банков по величине процентной ставки |
Число банков |
Сумма выданных кредитов, млн руб. |
|
|
всего |
в среднем на один банк |
|||
|
|
А |
1 |
2 |
3 |
|
1. |
11–15 |
7 |
168,1 |
24,0 |
|
2. |
15–19 |
13 |
200,5 |
15,4 |
|
3. |
19–23 |
7 |
54,4 |
7,8 |
|
4. |
23–27 |
3 |
6,8 |
2,3 |
|
Итого |
30 |
429,8 |
14,3 |
|
Данные табл. 2 показывают, что с ростом процентной ставки, под которую выдается кредит, средняя сумма кредита, выдаваемая одним банком, уменьшается. Это говорит о том, что между исследуемыми признаками существует обратная связь.
По способу построения группировки бывают простые и комбинационные. Простой называется группировка, в которой группы образованы только по одному признаку.
Комбинационной называется группировка, в которой образование групп производится по двум и более признакам, взятым в сочетании (комбинации). Рекомендуется сначала группировать единицы по качественным признакам, а затем – по количественным. Например, в группировке водителей автопарка по уровню квалификации (классу) и производительности труда вначале все водители делятся на две группы по классу, а затем внутри каждого класса производится деление по проценту выполнения плана (табл. 3).
Таблица 3.
Группировка водителей автопарка по классу и производительности труда
|
Квалификация водителя |
% выполнения плана |
Количество водителей, чел. |
Средний размер заработной платы, тыс.руб. |
|
I класс |
100–110 110 и более |
5 8 |
14,8 16,3 |
|
Итого по группе |
- |
13 |
- |
|
II класс |
100–110 110 и более |
7 10 |
13,7 14,5 |
|
Итого по группе |
- |
17 |
- |
|
ВСЕГО |
- |
30 |
- |
Построение статистических группировок включает следующие этапы:
1. Определение группировочного признака.
2. Определение числа групп.
3. Расчет ширины интервала группировки.
4. Выбор признаков, которые будут характеризовать выделенные группы.
Группировочным признаком (или основанием группировки) называется количественный или качественный признак, по которому проводится разбиение единиц совокупности на группы.
Число выделяемых групп зависит от вида группировочного показателя, степени его вариации и объема изучаемой совокупности.
Если группировочный признак качественный, то число групп будет равно числу вариантов этого признака. Например, группируя сотрудников по полу, мы получим 2 группы: сотрудники-мужчины и сотрудники-женщины.
При определении числа групп необходимо учесть размах вариации группировочного признака (R), который определяется по формуле:
R = хmax – хmin, (1)
где
Хmax – максимальное значение группировочного признака;
Хmin – минимальное значение группировочного признака.
Чем больше размах вариации группировочного признака, тем большее число групп может быть образовано. Однако при слишком большом их числе возникает проблема «пустых» групп, т.е. не содержащих ни одного объекта.
Число групп можно определить математически или экспертным путем. Математический способ предполагает использование формулы Стерджесса, которая дает хорошие результаты при большом объеме совокупности:
m = 1 + 3,322 ´ lg n, (2)
где
m – число выделяемых групп;
n – общее число единиц совокупности.
Полученное в результате расчетов значение округляют до целого числа по стандартным правилам округления.
Интервал – это значения признака, лежащие в определенных границах. Нижней границей называется наименьшее, а верхней границей – наибольшее значение признака в интервале. Ширина интервала – это разность между его верхней и нижней границами. По ширине интервалы группировки бывают равные (одинаковые) (табл. 4) и неравные (табл. 5).
Таблица 4.
Группы коммерческих банков по величине балансовой прибыли
|
№ группы |
Балансовая прибыль, млн руб. |
Число банков |
|
1. |
200–400 |
40 |
|
2. |
400–600 |
40 |
|
3. |
600–800 |
20 |
|
Итого |
100 |
|
Ширина каждого интервала составляет 200 млн руб:
400 – 200 = 600 – 400 = 800 – 600 = 200
Таблица 5.
Группы фирм по объему инвестиций
|
№ группы |
Объем инвестиций, млн руб. |
Число фирм |
|
1. |
10–20 |
5 |
|
2. |
20–40 |
10 |
|
3. |
40–80 |
12 |
|
Итого |
37 |
|
Ширина интервалов неодинакова:
· 20 – 10 = 10 млн руб.
· 40 – 20 = 20 млн руб.
· 80 – 40 = 40 млн руб.
Ширина равного интервала h определяется по следующей формуле:
![]() , (3)
, (3)
где
хmax, xmin – максимальное и минимальное значения признака в совокупности;
m – число выделяемых в совокупности групп.
Существуют следующие правила округления ширины интервала h:
· Если h имеет один знак до запятой (например: 0,67; 1,487; 3,82), полученные значения округляют до десятых (0,7; 1,5; 3,8.).
· Если h имеет две значащие цифры до запятой (например, 14,876), это значение округляют до целого числа (15).
· В случае, когда h является трех-, четырех- или еще более значимым числом, его величину следует округлить до ближайшего числа, кратного 100 или 50. Например, 652 следует округлить до 650 или до 700.
Интервалы группировки бывают также закрытыми (табл. 6.) и открытыми (табл. 7.).
Таблица 6.
Группировка страховых компаний по величине прибыли
|
Прибыль предприятия, млн руб. |
Число предприятий |
|
20–40 |
5 |
|
40–60 |
15 |
|
60–80 |
20 |
|
80–100 |
10 |
Таблица 7.
Группировка страховых компаний по величине прибыли
|
Прибыль предприятия, млн руб. |
Число предприятий |
|
до 40 |
5 |
|
40–60 |
15 |
|
60–80 |
20 |
|
80 и выше |
10 |
Если максимальные или минимальные значения сильно отличаются от других значений группировочного признака, то для определения ширины интервала используют значения, несколько превышающие минимум, и несколько меньшие, чем максимум. Полученную по формуле (3) величину округляют и используют в качестве ширины интервала, а первый и/или последний интервалы группировки открывают по верхней или нижней границе. Это делается для того, чтобы учесть в открытых интервалах единицы, имеющие аномально большие или малые значения группировочного признака.
Если значение признака у какой-то единицы совпадает с верхней границей интервала (например, 40 млн руб. (табл. 6) – это верхняя граница первого интервала (20–40) и нижняя граница второго (40–60)), то такая единица, как правило, относится к следующему интервалу (ко второму, (40–60)).
Если в основании группировки лежит дискретный признак, то нижняя граница каждого интервала (начиная со второго) берется равной верхней границе предыдущего интервала, увеличенной на 1. Например, группируя страховые компании по числу занятого персонала, можно выделить следующие группы (чел.): (100–150), (151–200), (201–300), (301–400).
Пример. Произведем группировку единиц совокупности, включающей 30 крупнейших по величине страховых премий страховых компаний Российской Федерации за 2012 год (табл. 8, по данным ФСФР, источник: www.fcsm.ru): Для удобства восприятия страховые компании расположены по убыванию величины страховых премий.
Показатели деятельности крупнейших страховых компаний РФ за 2012 год (по данным ФСФР)
|
№ п.п. |
Наименование страховой компании |
Город регистрации |
Страховые премии, млрд руб. |
Страховые выплаты, млрд руб. |
Количество заключенных договоров страхования, млн шт. |
|
1. |
РОСГОССТРАХ |
Люберцы |
97,4 |
41,2 |
26,84 |
|
2. |
СОГАЗ |
Москва |
76,0 |
29,8 |
1,03 |
|
3. |
ИНГОССТРАХ |
Москва |
67,8 |
43,8 |
6,79 |
|
4. |
РЕСО-ГАРАНТИЯ |
Москва |
51,8 |
28,3 |
6,46 |
|
5. |
АЛЬФАСТРАХОВАНИЕ |
Москва |
34,2 |
14,9 |
4,84 |
|
6. |
СОГЛАСИЕ |
Москва |
33,8 |
17,1 |
4,74 |
|
7. |
ВСК |
Москва |
33,6 |
19,4 |
2,95 |
|
8. |
АЛЬЯНС |
Москва |
25,1 |
15,3 |
4,58 |
|
9. |
ВТБ СТРАХОВАНИЕ |
Москва |
22,8 |
7,5 |
0,54 |
|
10. |
СТРАХОВАЯ ГРУППА МСК |
Москва |
20,0 |
14,8 |
4,17 |
|
11. |
ГРУППА РЕНЕССАНС СТРАХОВАНИЕ |
Москва |
18,0 |
13,2 |
2,00 |
|
12. |
МАКС |
Москва |
16,2 |
9,7 |
1,21 |
|
13. |
ДЖЕНЕРАЛИ ППФ СТРАХОВАНИЕ ЖИЗНИ |
Москва |
15,4 |
0,6 |
1,86 |
|
14. |
УРАЛСИБ |
Москва |
13,1 |
7,4 |
1,79 |
|
15. |
ЖАСО |
Москва |
11,8 |
8,2 |
11,75 |
|
16. |
КАПИТАЛ СТРАХОВАНИЕ |
Когалым |
9,4 |
2,7 |
0,08 |
|
17. |
РЕНЕССАНС ЖИЗНЬ |
Москва |
8,7 |
5,2 |
1,17 |
|
18. |
ЦЮРИХ |
Москва |
8,6 |
0,2 |
3,90 |
|
19. |
РОСГОССТРАХ-ЖИЗНЬ |
Москва |
8,4 |
1,7 |
0,35 |
|
20. |
ТРАНСНЕФТЬ |
Москва |
8,3 |
3,9 |
0,13 |
|
21. |
ЮГОРИЯ |
Ханты-Мансийск |
8,3 |
6,1 |
1,12 |
|
22. |
РУССКИЙ СТАНДАРТ СТРАХОВАНИЕ |
Москва |
8,1 |
0,7 |
2,53 |
|
23. |
АЛИКО |
Москва |
7,8 |
1,6 |
0,19 |
|
24. |
ЭНЕРГОГАРАНТ |
Москва |
7,8 |
2,9 |
0,70 |
|
25. |
ГУТА-СТРАХОВАНИЕ |
Москва |
7,4 |
3,5 |
1,52 |
|
26. |
АЛЬФАСТРАХОВАНИЕ-ЖИЗНЬ |
Москва |
6,1 |
0,1 |
1,71 |
|
27. |
ДЖЕНЕРАЛИ ППФ ОБЩЕЕ СТРАХОВАНИЕ |
Москва |
5,4 |
0,1 |
0,67 |
|
28. |
РОССИЯ |
Москва |
5,0 |
2,7 |
0,96 |
|
29. |
СУРГУТНЕФТЕГАЗ |
Сургут |
4,8 |
3,6 |
0,34 |
|
30. |
СОСЬЕТЕ ЖЕНЕРАЛЬ СТРАХОВАНИЕ ЖИЗНИ |
Москва |
4,6 |
0,1 |
0,39 |
|
|
Итого |
|
645,7 |
306,3 |
97,31 |
В качестве группировочного возьмем признак «размер страховых премий». Образуем четыре группы страховых компаний с равными интервалами. Величину интервала определим по формуле (3):
![]()
Согласно правилам округления в качестве ширины интервала возьмем величину 23. Обозначим границы групп:
|
1-я группа – 4,6–27,6
|
3-я группа – 50,6–73,6
|
|
2-я группа – 27,6–50,6 |
4-я группа – 73,6–96,6 |
Теперь необходимо подсчитать количество страховых компаний в каждой группе. В 1-ю группу войдут 23 компании (№№ от 30 до 8 включительно по исходным данным табл. 8), во 2-ю – три компании (№№ 7–5), в 3-ю – две (№№ 4–3) и в 4-ю – две (№№ 2–1).
Поскольку единичные и пустые группы в нашей группировке не обнаружены, можем переходить к завершающему этапу – построению итоговой группировочной таблицы, в которой все показатели будут приведены в разрезе построенных нами групп, а не по индивидуальным страховым компаниям, как в исходных данных. Для этого нужно просто суммировать индивидуальные значения показателей страховых компаний «страховые выплаты» и «количество заключенных договоров» по каждой группе и записать полученные суммы в соответствующие строки и столбцы итоговой таблицы (табл. 9).
Таблица 9.
Группировка крупнейших страховых компаний РФ по величине полученных страховых премий за 2012 год
|
Группы страховых компаний по величине страховых премий, млрд руб. |
Число страховых компаний |
Страховые выплаты, млрд руб. |
Количество заключенных договоров, млн шт. |
|
А |
1 |
2 |
3 |
|
4,6–27,6 |
23 |
111,8 |
43,66 |
|
27,6–50,6 |
3 |
51,4 |
12,53 |
|
50,6–73,6 |
2 |
72,1 |
13,25 |
|
73,6–96,6 |
2 |
71,0 |
27,87 |
|
Итого |
30 |
306,3 |
97,31 |
Структурная группировка страховых организаций на основе данных таблицы 9 будет иметь вид:
Группировка крупнейших страховых компаний РФ по величине полученных страховых премий за 2012 год
|
Группы страховых компаний по величине страховых премий, млрд руб. |
Число страховых компаний |
Страховые выплаты, % от общего размера |
Количество заключенных договоров, % от общего размера |
|
А |
1 |
2 |
3 |
|
4,6–27,6 |
23 |
36,50 |
44,87 |
|
27,6–50,6 |
3 |
16,78 |
12,88 |
|
50,6–73,6 |
2 |
23,54 |
13,62 |
|
73,6–96,6 |
2 |
23,18 |
28,64 |
|
Итого |
30 |
100,00 |
100,00 |
Из таблицы 10 видно, что больше трети (36,50 %) всех страховых выплат и чуть менее половины всех заключенных договоров (44,87 %) приходится на группы страховых компаний с объемом страховых премий от 4,6 до 27,6 млрд руб.
Аналитическая группировка (табл. 11) показывает, что размер страховых премий и количество заключенных договоров находятся между собой в прямой зависимости. А вот величина страховых выплат не имеет четкой прямой взаимосвязи с размером страховых премий, что можно объяснить различием подходов к оценке и возмещению страховых случаев, а также особенностями рыночных стратегий развития и привлечения клиентов у крупнейших страховых компаний.
Аналитическая группировка крупнейших страховых компаний РФ по величине полученных страховых премий за 2012 год
|
Группы страховых компаний по величине страховых премий, млрд руб. |
Число страховых компаний |
Страховые выплаты, млрд руб. |
Количество заключенных договоров, млн шт. |
||
|
всего |
в среднем на 1 страховую компанию |
всего |
в среднем на 1 страховую компанию |
||
|
4,6–27,6 |
23 |
111,8 |
4,9 |
43,66 |
1,90 |
|
27,6–50,6 |
3 |
51,4 |
17,1 |
12,53 |
4,18 |
|
50,6–73,6 |
2 |
72,1 |
36,1 |
13,25 |
6,63 |
|
73,6–96,6 |
2 |
71,0 |
35,5 |
27,87 |
13,94 |
|
Итого |
30 |
306,3 |
10,2 |
97,31 |
3,20 |
Ряд распределения представляет собой простейшую группировку, в которой каждая выделенная группа характеризуется только количеством входящих в нее единиц совокупности. В рассмотренном нами примере с группировкой страховых организаций по величине страховых премий мы также получили ряд распределения – он записан в графах А и 1 таблицы 11.
Различают атрибутивные и вариационные ряды распределения (рис. 13).
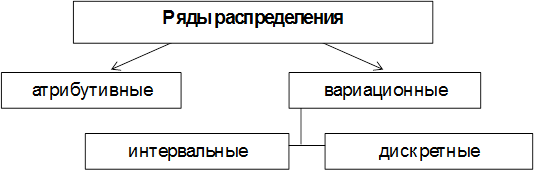
Рис. 13. Виды рядов распределения
Атрибутивными называют ряды распределения, построенные по качественным признакам.
Вариационными называют ряды распределения, построенные по количественному признаку. Вариационный ряд состоит из двух элементов: вариантов и частот.
Вариантами называются отдельные значения признака. Варианты признака обозначаются как Хi. Частотами называются численности отдельных вариант или каждой группы вариационного ряда. Частоты показывают, как часто встречаются те или иные значения признака в изучаемой совокупности и обозначаются через fi. Сумма всех частот определяет объем совокупности. Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100 %.
Дискретный вариационный ряд характеризуют распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Например, группы студентов по баллу в сессию (табл. 12).
таблица 12.
Распределение студентов по баллам в сессию (данные условные)
|
Балл (оценка) |
Количество студентов |
Удельный вес студентов, % |
|
5 |
34 |
29,82 |
|
4 |
37 |
32,46 |
|
3 |
33 |
28,95 |
|
2 |
10 |
8,77 |
|
Итого |
114 |
100,00 |
Интервальный вариационный ряд распределения – это ряд распределения, в котором группировочный признак задан интервалами значений. Например, распределение консалтинговых фирм по величине прибыли (табл. 13).
Таблица 13.
Ряд распределение консалтинговых фирм по величине прибыли за 2012 г. (данные условные)
|
Прибыль, млн. руб. |
Количество фирм |
|
20–40 |
5 |
|
40–60 |
15 |
|
60–80 |
20 |
|
80–100 |
10 |
Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строят полигон или гистограмму.
Полигон используется для изображения дискретных вариационных рядов. По оси абсцисс (Х) в одинаковом масштабе откладываются значения признака, а по оси ординат (Y) – частоты. Полученные на пересечении осей X и Y точки соединяются прямыми линиями, в результате чего получают ломаную линию, называемую полигоном распределения (рис. 14).
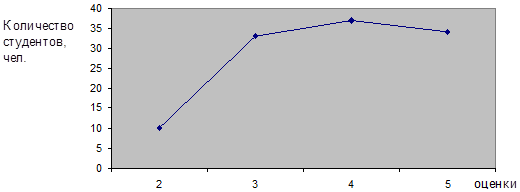
Рис. 14. Полигон распределения студентов по баллам в сессию (см. табл. 12)
Гистограмма распределения применяется для изображения интервального вариационного ряда. При ее построении на оси Х откладываются величины интервалов, а на оси Y – частоты, которые изображаются прямоугольниками, построенными на соответствующих интервалах. Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить прямыми линиями (рис. 15).
При построении гистограммы распределения вариационного ряда с неравными интервалами по оси Y наносят не частоты, а плотность распределения признака в соответствующих интервалах. Плотность распределения – это частота, рассчитанная на единицу ширины интервала.

Рис. 15. Гистограмма и полигон распределения консалтинговых фирм по величине прибыли за 2012 г. (см. табл. 13)
1. В чем заключается основная задача метода группировки?
2. Какие виды группировок применяются?
3. Что такое ряд распределения и чем он отличается от группировки?
4. Как можно определить число групп при группировке данных?
5. Может ли качественный признак являться основанием группировки?
6. В чем отличие ряда распределения от статистической групировки?
7. Можно ли построить гистограмму по данным о распределении семей по числу детей?
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Задание 1.
Вы начали кампанию по улучшению качества продукции на вашей бумажной фабрике и для этих целей собрали большое количество докладных записок о проблемах потребителей. Представленная в каждой докладной записке проблема кодируется следующим образом: А – отсутствие бумаги; Б – бумага слишком толстая; С – бумага слишком тонкая; D – ширина бумаги не соответствует стандарту; E – не тот цвет бумаги; F – края бумаги крупно обрезаны. Собранная информация приведена ниже:
А, А, E, A, A, A, B, A, A, A, B, A, B, F, F, A, A, A, A, A, B, A, A, A, C, D, F, A, A, E, A, C, A, A, A, F, F, D.
Обобщите этот набор данных, вычислив (с точностью до 0,01) процент проблем каждого вида в общем количестве проблем.
Задание 2.
По данным о ходе приватизации жилых помещений в РФ (табл. 14) постройте группировку областей Центрального федерального округа по % приватизированных жилых помещений от общего числа жилых помещений, подлежащих приватизации. Выделите три группы областей с равными по ширине интервалами. При помощи структурной группировки по каждой выделенной вами группе областей определите (с точностью до 0,01), долю (в %) приватизированных в 2011 году жилых помещений в целом по группе от общего числа приватизированных в 2011 году жилых помещений Центрального федерального округа. Результаты оформите в итоговой таблице 15, дав таблице название.
Таблица 14.
Приватизация жилых помещений в РФ по состоянию на 01 января 2012 г.
|
|
Приватизировано жилых помещений в 2011 г., тыс. ед. |
Приватизировано жилых помещений с начала приватизации на 1 января 2012 г. |
|
|
Всего, тыс. ед. |
в % от общего числа жилых помещений, подлежащих приватизации |
||
|
Российская Федерация |
340,1 |
28897,4 |
75,8 |
|
Центральный федеральный округ |
98,2 |
7962,1 |
73,5 |
|
Белгородская область |
2,3 |
235,2 |
86,6 |
|
Тверская область |
4,6 |
346,3 |
81,0 |
|
Брянская область |
2,8 |
224,0 |
80,1 |
|
Рязанская область |
2,4 |
254,4 |
80,1 |
|
Орловская область |
1,9 |
138,6 |
79,4 |
|
Ярославская область |
4,0 |
346,6 |
79,2 |
|
Липецкая область |
2,0 |
213,9 |
77,6 |
|
Воронежская область |
7,5 |
366,1 |
76,7 |
|
Владимирская область |
4,1 |
371,2 |
76,0 |
|
Ивановская область |
2,6 |
257,9 |
75,7 |
|
Тамбовская область |
1,7 |
175,9 |
75,6 |
|
Калужская область |
3,0 |
243,3 |
75,5 |
|
Костромская область |
2,2 |
166,5 |
73,6 |
|
Тульская область |
4,5 |
406,1 |
73,1 |
|
Смоленская область |
2,7 |
232,3 |
72,5 |
|
г. Москва |
28,4 |
2284,4 |
71,9 |
|
Московская область |
19,6 |
1523,7 |
67,9 |
|
Курская область |
2,1 |
175,6 |
65,3 |
Таблица 15.
|
Группы областей по % приватизированных жилых помещений от общего числа подлежащих приватизации |
Количество областей ЦФО |
Приватизировано жилых помещений за 2011 год |
|
|
Всего, тыс. ед. |
В % от общего объема |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 3.
По данным табл. 14 постройте группировку областей Центрального федерального округа (ЦФО), выделив две группы областей – области, в которых % приватизированных жилых помещений ниже, чем в общем по ЦФО, и области, в которых % приватизированных жилых помещений выше, чем в общем по ЦФО. При помощи структурной группировки по каждой группе определите общее количество приватизированного жилья с начала приватизации (в тыс. ед. и в %) с точностью до 0,01. Результаты оформите в таблице 16, дав ей название.
Таблица 16.
|
Группы областей по % приватизированных жилых помещений от общего числа подлежащих приватизации |
Количество областей ЦФО |
Приватизировано жилых помещений с начала приватизации на 1 января 2012 г. |
|
|
Всего, тыс. ед. |
В % от общего количества |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цель изучения темы состоит в формировании системы знаний и компетенций о видах статистических показателей, выраженных абсолютными и относительными величинами, методике их расчета и анализа.
В результате успешного освоения темы Вы:
Узнаете:
· классификацию основных статистических показателей;
· какие показатели относятся к абсолютным;
· какие существуют единицы измерения показателей;
· как рассчитывают относительные показатели.
Приобретете компетенции:
· владение методами теоретического и экспериментального исследования;
· понимание роли и значения информации в развитии современного общества и экономических знаний;
· владение основными методами, способами и средствами получения, хранения, переработки информации;
· способность оценивать воздействие макроэкономической среды на функционирование организаций;
· способность анализировать финансовую отчетность и принимать обоснованные решения;
· владение методами расчета и анализа статистических показателей, выраженных абсолютными и относительными величинами.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· индивидуальные абсолютные показатели;
· сводные абсолютные показатели;
· относительный показатель динамики;
· относительный показатель плана;
· относительный показатель реализации плана;
· относительный показатель структуры;
· относительный показатель координации;
· относительный показатель интенсивности;
· относительный показатель уровня экономического развития;
· относительный показатель сравнения.
Вопросы темы:
1. Абсолютные показатели.
2. Относительные показатели.
Теоретический материал по теме
Исходной формой статистических показателей являются показатели в абсолютном выражении, или абсолютные величины. Статистические показатели в форме абсолютных величин характеризуют размеры изучаемых статистикой процессов и явлений, а именно: их массу, площадь, объем, протяженность, отражают их временные характеристики, а также могут представлять объем совокупности, т.е. число составляющих ее единиц.
Индивидуальные абсолютные показатели получают непосредственно при сборе данных как результат замера, взвешивания, подсчета и оценки интересующего количественного признака у конкретного объекта – человека, предприятия, домохозяйства. Индивидуальные абсолютные показатели могут рассчитываться как разность. Например: разность между численностью работников предприятия на конец и на начало года, разность между выручкой от реализации предприятия и суммой затрат.
Сводные абсолютные показатели характеризуют общий объем признака, объем совокупности или ее части. Их получают в результате сводки и группировки индивидуальных значений. К таким показателям относятся общая численность занятых в отрасли, совокупные активы коммерческих банков региона и т.п.
Абсолютные статистические показатели всегда имеют единицы измерения. Различают натуральные, стоимостные и трудовые единицы измерения (рис. 16).

Рис. 16. Виды единиц измерения абсолютных показателей
В международной практике используются такие натуральные единицы измерения, как тонны, килограммы, квадратные, кубические и простые метры, мили, километры, галлоны, литры, штуки и т.д. Например, в России за 2011 г. было добыто 512 млн т нефти и 671 млрд м3 газа.
В группу натуральных также входят условно-натуральные измерители, используемые в тех случаях, когда какой-либо продукт имеет несколько разновидностей и общий объем можно определить только исходя из общего для всех разновидностей потребительского свойства. Так, различные виды органического топлива переводятся в условное топливо с теплотой сгорания 29,3 МДж/кг (7000 ккал/кг), мыло разных сортов – в условное мыло с 40 %-ным содержанием жирных кислот, консервы различного объема – в условные консервные банки объемом 353,4 см3 и т.д. Перевод в условные единицы измерения осуществляется на основе специальных коэффициентов, рассчитываемых как отношение потребительских свойств отдельных разновидностей продукта к эталонному значению. Так, например, 100 т торфа, теплота сгорания которого – 24 МДж/кг, будут эквивалентны 81,9 т условного топлива (100 * 24,0 / 29,3), а 100 т нефти при теплоте сгорания 45 МДж/кг будут оцениваться в 153,6 т условного топлива (100 * 45,0/29,3).
В отдельных случаях для характеристики какого-либо явления или процесса используется произведение двух единиц. Например, грузооборот и пассажирооборот, оцениваемые соответственно в тонно-километрах и пассажиро-километрах.
В условиях рыночной экономики наибольшее применение имеют стоимостные единицы измерения, позволяющие получить денежную оценку социально-экономических явлений и процессов. Так, одним из важнейших стоимостных показателей в системе национальных счетов, характеризующим общий уровень развития экономики страны, является валовой внутренний продукт, который в России за 2012 год составил 62 599,1 млрд руб. в текущих ценах (в номинальном выражении).
При анализе и сопоставлении стоимостных показателей необходимо иметь в виду, что в условиях высоких или относительно высоких темпов инфляции они становятся несопоставимыми. Так, сравнивать ВВП России в текущих ценах за 2012 год с его величиной, например, за 1995 год нецелесообразно, так как содержание рубля за этот период существенно изменилось. Для подобных сравнений осуществляют пересчет показателей в сопоставимые цены.
К трудовым единицам измерения, позволяющим учитывать общие затраты труда на предприятии, трудоемкость отдельных операций технологического процесса, относятся человеко-дни и человеко-часы.
Почему важно всегда учитывать единицы измерения показателей? Потому что один и тот же показатель может принимать различные количественные выражения в зависимости от выбранных единиц измерения. Например, партия продукции может характеризоваться следующими величинами: 1000 штук упаковок или 200 килограмм в натуральном выражении; 350 тыс. рублей – в стоимостном выражении; 50 чел.-ч. – в трудовых единицах измерения.
Единство единиц измерения позволяет сравнивать различные объекты, определять соотношения между ними, изучать структуру общественных явлений и процессов по различным показателям.
Относительный показатель представляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических процессов и явлений. Без относительных показателей невозможно измерить интенсивность развития изучаемого явления во времени, оценить уровень развития одного явления на фоне других, осуществить пространственно-территориальные сравнения, в том числе и на международном уровне.
Абсолютный показатель, находящийся в числителе, называется текущим, или сравниваемым. Показатель, с которым производится сравнение и который находится в знаменателе, называется основанием, или базой сравнения. Рассчитываемая таким образом относительная величина показывает, во сколько раз сравниваемый абсолютный показатель больше базисного, какую составляет от него долю, или сколько единиц первого приходится на 1, 100, 1000 и т.д. единиц второго.
Относительные показатели могут:
· выражаться в коэффициентах (долях единицы);
· выражаться в процентах (%);
· выражаться в промилле (%0);
· выражаться в продецимилле (%00);
· быть именованными числами.
Если база сравнения принимается за 1, то относительный показатель выражается в коэффициентах, если база принимается за 100, 1000 или 10000, то показатель соответственно выражается в (%), (%0) и (%00).
Именованный относительный показатель получается в результате соотнесения разноименных абсолютных показателей. Его наименование представляет собой сочетание наименований единиц измерения сравниваемых показателей.
Все используемые на практике относительные статистические показатели можно подразделить на следующие виды:
1) относительные показатели динамики;
2) относительные показатели плана;
3) относительные показатели реализации плана;
4) относительные показатели структуры;
5) относительные показатели координации;
6) относительные показатели интенсивности и уровня экономического развития;
7) относительные показатели сравнения.
Относительный показатель динамики (ОПД).
ОПД получают путем деления величины показателя, относящейся к одному временному промежутку (моменту), на величину этого же показателя за другой, как правило, прошедший промежуток или момент времени. Рассчитывая ОПД, мы сопоставляем величины одного и того же показателя, взятые за различные временные промежутки.
ОПД представляет собой отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) к уровню этого же процесса или явления в прошлом:
![]() (4)
(4)
Рассчитанная таким образом величина показывает, во сколько раз текущий уровень превышает предшествующий (базисный) или какую долю от последнего составляет. Данный показатель может быть выражен кратным отношением или переведен в проценты.
Различают относительные показатели динамики с постоянной и переменной базой сравнения. Если сравнение осуществляется с одним и тем же базисным уровнем, например первым годом рассматриваемого периода, получают относительные показатели динамики с постоянной базой (базисные). При расчете относительных показателей динамики с переменной базой (цепных) сравнение осуществляется с предшествующим уровнем, т.е. основание относительной величины последовательно меняется.
Для примера воспользуемся данными таблицы 17.
Таблица 17.
Число абонентских устройств радиотелефонной (сотовой) связи в РФ в 2008–2011 гг. (млн шт., на конец года)
|
Год |
2008 |
2009 |
2010 |
2011 |
|
Объем производства |
199,5 |
230,5 |
237,7 |
256,1 |
Рассчитаем ОПД с переменной и постоянной базой сравнения:
|
Переменная база сравнения (цепные показатели) |
Постоянная база сравнения (базисные показатели) |
|
|
|
|
|
|
|
|
|
Относительные показатели динамики с переменной и постоянной базой сравнения взаимосвязаны между собой следующим образом: произведение всех относительных показателей с переменной базой равно относительному показателю с постоянной базой за исследуемый период. Так, для рассчитанных показателей (предварительно переведя их из процентов в коэффициенты) получим:
1,1554 * 1,0312 * 1,0770 = 1,2832
Относительные показатели плана и реализации плана. Все субъекты финансово-хозяйственной деятельности, от небольших индивидуальных частных предприятий и до крупных корпораций, осуществляют как оперативное, так и стратегическое планирование, а также сравнивают реально достигнутые результаты с ранее намеченными. Для этих целей используются относительные показатели плана (ОПП) и реализации плана (ОПРП):
![]() (5)
(5)
![]() (6)
(6)
ОПП характеризует относительную высоту планового уровня, т.е. во сколько раз намечаемый размер показателя превысит фактически достигнутый уровень или сколько процентов от него составит. ОПРП показывает, на сколько % выполнено плановое задание, то есть отражает фактический достигнутый объем производства или реализации в процентах или коэффициентах по сравнению с плановым уровнем.
Предположим, оборот торговой фирмы в 2011 г. составил 5,0 млн руб. Исходя из проведенного анализа складывающихся на рынке тенденций, руководство фирмы считает реальным в следующем году довести оборот до 5,6 млн руб. В этом случае относительный показатель плана, представляющий собой отношение планируемой величины к фактически достигнутой, составит 112,0 % (5,6 : 5,0 * 100 %). Предположим теперь, что фактический оборот фирмы за 2012 г. составил 5,7 млн руб. Тогда относительный показатель реализации плана, определяемый как отношение фактически достигнутой величины к ранее запланированной, составит 101,8 % (5,7 : 5,6 * 100 %).
Между относительными показателями плана, реализации плана и динамики существует следующая взаимосвязь:
ОПП * ОПРП = ОПД (7)
В нашем примере: 1,120 * 1,018 =
1,140, или ![]()
Основываясь на этой взаимосвязи, по любым двум известным величинам всегда можно определить третью неизвестную величину.
Относительный показатель структуры (ОПС) представляет собой соотношение структурных частей изучаемого объекта и их целого:
![]() (8)
(8)
ОПС выражается в долях единицы или в процентах. Рассчитанные величины, соответственно называемые долями или удельными весами, показывают, какой долей обладает или какой удельный вес имеет та или иная часть в общем итоге.
Рассмотрим структуру привлеченных кредитными организациями вкладов в РФ в 2012 г. (табл. 18):
Таблица 18.
Вклады (депозиты) юридических и физических лиц в рублях и иностранной валюте,
привлеченные кредитными организациями в РФ в 2012 г.
(на начало года; млрд руб.)
|
|
Объем |
|
|
млрд руб. |
% к итогу |
|
|
Вклады всего |
19 235 |
100,0 |
|
в том числе: |
||
|
- юридических лиц |
7 382 |
38,4 |
|
- физических лиц |
11 853 |
61,6 |
Рассчитанные в последней графе таблицы проценты представляют собой относительные показатели структуры (в данном случае – удельные веса). Их анализ показывает, что доля вкладов юридических лиц в общем объеме привлеченных кредитными организациями вкладов в 2012 г. составляет 38,4 % (7 382 : 19 235 * 100), а вклады физических лиц составляют 61,6 % (11 853 : 19 235 * 100) от общего объема всех депозитов, привлеченных кредитными организациями.
Следует обратить внимание, что сумма удельных весов, характеризующих структурные части одной совокупности, всегда должна быть строго равна 100 % или 1.
Относительный показатель координации (ОПК) представляет собой отношение одной части совокупности к другой части этой же совокупности:
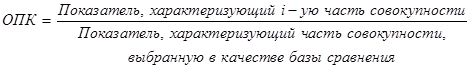 (9)
(9)
В качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. В результате узнают, во сколько раз данная часть больше базисной или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу (иногда – на 100, 1000 и т.д. единиц) базисной структурной части. Так, на основе данных таблицы 18 мы можем вычислить, что на каждый рубль привлеченных вкладов физических лиц в 2012 г. приходился 0,62 руб. вкладов юридических лиц (7 382 : 11 853), а если за базу сравнения принять объем вкладов юридических лиц и рассчитать показатель координации (11 853 : 7 382 = 1,61), то мы узнаем, что в 2012 г. объем вкладов физических лиц был в 1,61 раза больше объема вкладов юридических лиц, и на 1 руб. вкладов юридических лиц приходился 1,61 руб. вкладов физических лиц.
Относительный показатель интенсивности (ОПИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды:
![]() (10)
(10)
Данный показатель получают сопоставлением уровней двух взаимосвязанных в своем развитии явлений. Поэтому наиболее часто он представляет собой именованную величину, но может быть выражен и в процентах, промилле, продецимилле.
Например, для определения уровня обеспеченности населения легковыми автомобилями рассчитывается число автомашин, приходящихся на 100 семей, для определения плотности населения рассчитывается число людей, приходящихся на 1 кв. км.
Так, на конец 2011 г. общая численность мигрантов, прибывших в РФ, составляла 320,1 тыс. чел., а численность населения РФ – 143,0 млн чел. Отсюда следует, что ОПИ, характеризующий в данном случае уровень миграционного прироста, составлял 0,00022 = 0,3201 : 143,0, или на каждые 10 000 человек населения приходилось 22 человека мигрантов.
Разновидностью относительного показателя интенсивности является относительный показатель уровня экономического развития, характеризующий производство продукции в расчете на душу населения и играющий важную роль в оценке развития экономики государства или региона. В расчетах используют среднюю численность населения (например, за один год).
Например, размер ВВП России в 2012 году составил 62 599,1 млрд руб. в текущих ценах. Для того чтобы сделать вывод об уровне развития экономики, необходимо сопоставить его со среднегодовой численностью населения страны (143,0 млн чел),. В результате размер ВВП на душу населения в 2012 г. составляет 437,8 тыс. руб. (62 599,1 : 143,0).
Относительный показатель сравнения (ОПСр) представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.):
![]() (11)
(11)
Для выражения данного показателя могут использоваться как коэффициенты, так и проценты.
Например, согласно официальным статистическим данным, в 2012 году в РФ самые высокие среднедушевые денежные доходы были у населения Центрального федерального округа – 29 574,7 руб., в том числе в г. Москве – 48 343,4 руб., а самые низкие у населения Северо-Кавказского федерального округа – 17 131,9 руб. Таким образом, можно сделать вывод, что размер среднедушевых денежных доходов населения СКФО в 1,7 раз ниже, чем в ЦФО, и в 2,8 раз ниже, чем в г. Москве.
1. Что характеризуют абсолютные показатели?
2. Почему важно всегда учитывать единицы измерения показателей и какие виды единиц измерения существуют?
3. Какие различают виды относительных показателей?
4. В какие единицах измерения выражаются относительные показатели?
5. Укажите, к какому виду показателей относятся показатели, приведенные ниже:
· коэффициент рождаемости (отношение числа родившихся к общей численности населения);
· отношение величины прибыли предприятия за II квартал 2013 года к величине прибыли за I квартал 2013 года;
· количество рабочих-ремонтников, приходящихся на 10 водителей автобусного парка;
· отношение величины фактических затрат на производство за май 2013 года к запланированному ранее на май размеру затрат.
6. На сколько процентов реализован план по выпуску продукции, если планировалось увеличить выпуск на 14 %, а по итогам месяца выпуск увеличился на 19,7 %?
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Методологические положения по статистике. – М.: Госкомстат России, 2010.
5. Курс социально-экономической статистики: учебник для вузов / Под ред. М.Г. Назарова. – М.: Финстатинформ, ЮНИТИ–ДАНА, 2005.
Задание 1.
Число корпоративных клиентов ОАО АКБ «Х» на 1 января 2013 г. составило 50 000. Руководство банка приняло решение о расширении бизнеса и объявило о необходимости увеличения клиентской базы на менее чем на 2,5 % за каждые полгода. Определите, на сколько минимально должно увеличиться количество корпоративных клиентов банка к концу 2013 г. при условии выполнения требуемого руководством размера увеличения клиентской базы?
Задание 2.
Предприятие планировало увеличить выпуск продукции в первом полугодии 2013 г. по сравнению со вторым полугодием 2012 г. на 15 %. Фактический же объем продукции составил 135,7 % от уровня второго полугодия 2012 г. Определите, на сколько процентов реализовано плановое задание.
Задание 3.
По данным о занятости населения РФ определите, как изменился уровень безработицы населения (отношение числа безработных к численности экономически активного населения) за период с 2000 по 2011 гг. в абсолютном выражении и в %. Уровень безработицы рассчитайте в промилле – на 1000 человек экономически активного населения.
Численность экономически активного населения, занятых и безработных в РФ (тысяч человек)
|
|
2000 |
2011 |
|
Численность экономически активного населения, всего |
72332 |
75752 |
|
в том числе: |
|
|
|
занятые в экономике |
65273 |
70732 |
|
безработные |
7059 |
5020 |
Задание 4.
Имеются следующие данные о внешнеторговом обороте России (млрд долл. США):
|
|
2006 |
2011 |
||
|
млрд долл. США |
В % |
млрд долл. США |
В % |
|
|
Внешнеторговый оборот всего, |
467,9 |
|
845,8 |
|
|
в том числе: |
|
|
|
|
|
Экспорт |
303,6 |
|
522,0 |
|
|
Импорт |
164,3 |
|
323,8 |
|
|
Расчет показателей координации |
||||
|
ОПК Экспорт/Импорт |
|
|
||
|
ОПК Импорт/Экспорт |
|
|
||
а) Вычислите относительные показатели структуры и занесите их в соответствующие графы таблицы.
б) При помощи показателей координации определите, сколько долларов США экспорта приходилось на 1 доллар США импорта и сколько долларов США импорта приходилось на 1 доллар экспорта в 2006 и 2011 гг. Результаты расчетов изложите в таблице.
Цель изучения темы состоит в формировании системы знаний о категории и видах средних величин, овладении методами расчета и интерпретации статистических показателей, выраженных средними величинами.
В результате успешного освоения темы Вы:
Узнаете:
· что такое средняя величина и для чего она применяется;
· что такое логическая формула средней величины;
· какие виды средних величин существуют и как они рассчитываются;
· что такое структурные средние и что они характеризуют;
· как рассчитываются структурные средние.
Приобретете компетенции:
· владение методами теоретического и экспериментального исследования;
· понимание роли и значения информации в развитии современного общества и экономических знаний;
· владение основными методами, способами и средствами получения, хранения, переработки информации;
· способность оценивать воздействие макроэкономической среды на функционирование организаций;
· способность анализировать финансовую отчетность и принимать обоснованные решения;
· способность оценивать эффективность использования различных систем учета и распределения затрат, иметь навыки калькулирования и анализа себестоимости продукции;
· способность обосновывать решения в сфере управления оборотным капиталом;
· умение обоснованно выбирать вид средней величины в зависимости от особенностей исходной числовой информации;
· владение методами расчета и анализа статистических показателей в форме средних величин и формулирования обоснованных выводов на основе рассчитанных значений.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· средняя величина;
· определяющее свойство средней величины;
· исходное соотношение средней величины (ИСС);
· средняя арифметическая простая;
· средняя арифметическая взвешенная;
· средняя гармоническая взвешенная;
· средняя геометрическая;
· средняя квадратическая;
· средняя хронологическая;
· мода;
· медиана.
Вопросы темы:
1. Сущность и исходное соотношение средней величины.
2. Средняя арифметическая и ее свойства.
3. Средняя гармоническая, квадратическая и геометрическая.
4. Средняя хронологическая.
5. Структурные средние.
Теоретический материал по теме
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина.
Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности колеблются под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время в отдельные дни и на отдельных биржах эти акции в силу обстоятельств могут продаваться по более высокому или заниженному курсу. В средней взаимопогашаются случайные отклонения, и учитываются изменения, вызванные действием основных факторов. Это позволяет средней отражать типичный уровень признака, независимо от индивидуальных особенностей отдельных единиц.
Категорию средней можно раскрыть через понятие определяющего свойства. Согласно этому понятию средняя, являясь обобщающей характеристикой всей совокупности, ориентируется на определенную величину, связанную со всеми единицами изучаемой совокупности. Эту величину можно представить в виде функции:
f (х1, х2, ..., хn) (12)
Если в функции (12) все величины х1,
х2, ... , хn заменить их средней величиной
![]() , то значение
этой функции должно остаться прежним:
, то значение
этой функции должно остаться прежним:
![]() (13)
(13)
На практике среднюю можно определить через исходное соотношение средней (ИСС) или ее логическую формулу:
![]()
Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней. Например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:
![]()
Средний размер одного вклада в банк определяется как:
![]()
Чаще других на практике используется средняя арифметическая, которая, как и все средние, может быть простой или взвешенной.
Средняя арифметическая простая используется в тех случаях, когда расчет осуществляется по несгруппированным данным.
Предположим, шесть торговых предприятий фирмы имеют следующий объем товарооборота за месяц:
|
Торговое предприятие |
1 |
2 |
3 |
4 |
5 |
6 |
|
Товарооборот (млн руб.) |
25 |
18 |
27 |
32 |
15 |
21 |
Среднемесячный товарооборот в расчете на одно предприятие определяет следующее исходное соотношение:
![]()
Используя условные обозначения, запишем формулу средней арифметической простой:
![]() (14)
(14)
Подставив в формулу данные, рассчитаем среднюю:
![]()
Средняя арифметическая взвешенная используется, когда все или отдельные значения осредняемого признака повторяются, т.е. для расчета средней величины по сгруппированным данным или рядам распределения.
Рассмотрим следующий условный пример.
Таблица 19.
Сделки по акциям эмитента «ХХХ» за торговую сессию
|
Сделка |
Курс продажи, руб. |
Количество проданных акций, шт. |
Удельный вес, % |
|
1. |
420 |
700 |
37,8 |
|
2. |
440 |
200 |
10,8 |
|
3. |
410 |
950 |
51,4 |
Определим по данному дискретному вариационному ряду средний курс продажи 1 акции, что можно сделать, используя исходное соотношение:
![]()
Чтобы получить общую сумму сделок, необходимо по каждой сделке курс продажи (Хi) умножить на количество проданных акций (fi) и полученные произведения сложить:
![]()
Расчет среднего курса продажи произведен по формуле средней арифметической взвешенной:
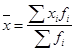 (15)
(15)
В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Если для расчета средней по данным табл. 19 использовать удельные веса, преобразовав формулу (15), получим:
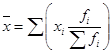 (16)
(16)
Или можно выразить удельный вес в долях единицы:
![]()
При расчете средней по интервальному вариационному ряду от интервалов переходят к их серединам. При этом ширина открытых интервалов (первого и последнего) условно приравнивается к ширине интервалов, примыкающих к ним (второго и предпоследнего). Рассмотрим следующий пример (табл. 20).
Таблица 20.
Распределение сотрудников предприятия по возрасту
|
Возраст (лет) |
Число сотрудников (чел.) |
|
до 25 |
8 |
|
25–30 |
32 |
|
30–40 |
68 |
|
40–50 |
49 |
|
50–60 |
21 |
|
60 и более |
3 |
|
Итого: |
181 |
Для определения среднего возраста персонала найдем середины возрастных интервалов: 22,5 (для интервала до 25), 27,5 (для интервала 25–30), 35,0 (для интервала 30–40), 45,0 (для интервала 40–50), 55,0 (для интервала 50–60), 65,0 (для интервала 60 и более).
Используя среднюю арифметическую взвешенную, определим средний возраст работников данного предприятия:
![]()
На практике наиболее часто встречаемая при расчете средних ошибка заключается в игнорировании весов. Например, имеются следующие данные:
Таблица 21.
Себестоимость продукции «Z»
|
Предприятие |
Себестоимость единицы продукции, руб. |
|
1. |
37 |
|
2. |
39 |
Можно ли по имеющимся данным определить среднюю себестоимость единицы продукции по двум предприятиям вместе? Можно, но только в том случае, когда объемы производства данной продукции на двух предприятиях совпадают. Тогда средняя себестоимость составит 38,0 руб. ((37 + 39) : 2). Однако если на первом предприятии произведено 50 единиц продукции, а на втором – 700, для расчета средней себестоимости потребуется уже средняя арифметическая взвешенная:
![]()
Вывод: использовать среднюю арифметическую невзвешенную можно только тогда, когда точно установлено отсутствие весов или их равенство.
Средняя арифметическая обладает математическими свойствами, которые более полно раскрывают ее сущность и в ряде случаев используются для ее расчета. Рассмотрим эти свойства.
1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:
![]() (17)
(17)
Проверим свойство на примере расчета среднего курса продажи акций (табл. 19). За счет округления среднего курса правая и левая части равенства в данном случае будут несколько отличаться:
417,03 ´ 1 850 = 420 ´ 700 + 440 ´ 200 + 410 ´ 950
2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:
![]() (18)
(18)
Для нашего примера:
(420 – 417,03) ´ 700 + (440 – 417,03)
´ 200 + (410 – 417,03) ´ 950 ![]() 0
0
3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С.
Рассмотрим это свойство на упрощенном примере по ряду
данных xi = 3, 4, 5. Средняя величина для данного
ряда равна 4. Рассчитаем сумму квадратов отклонений от ![]() = 4
и от величины С, приняв ее за вариант xi = 3:
= 4
и от величины С, приняв ее за вариант xi = 3:
|
|
|
|
|
|
|
( |
|
3 |
3 – 4 = -1 |
(-1)2= 1 |
|
3 |
3 – 3 = 0 |
(0) 2= 0 |
|
4 |
4 – 4 = 0 |
02 = 0 |
|
4 |
4 – 3 = 1 |
1 2 = 1 |
|
5 |
5 – 4 = 1 |
12 = 1 |
|
5 |
5 – 3 = 2 |
22 = 4 |
|
|
|
|
|
|
|
|
|
Итого |
- |
2 |
|
Итого |
0 |
5 |
![]()
Каким бы большим или малым мы ни брали число С, сумма квадратов отклонений индивидуальных значений признака от нее всегда будет больше суммы квадратов их отклонений от средней на величину:
![]() (19)
(19)
4. Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину А:
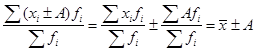 (20)
(20)
Так, если все курсы продажи акций увеличить на 15 руб., то средний курс также увеличится на 15 руб.:
![]()
5. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз:
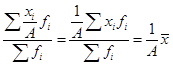 (21)
(21)
Предположим, курс продажи в каждом случае вырос в 2 раза. Тогда и средний курс также увеличится на 100 %:
![]()
6. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:
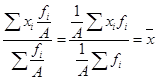 (22)
(22)
Так, в нашем примере удобнее было бы рассчитывать среднюю, предварительно поделив все веса на 100:
![]()
Средняя гармоническая взвешенная используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель. Другими словами, когда в исходных данных нам известны индивидуальные усредняемые значения хi, но нет прямой информации о количестве объектов, т.е. о частотах fi, однако эти данные можно получить при помощи простых расчетов. Например, известна цена 1 кг товара – 50 руб. и общий объем его реализации – 250 руб. Прямого указания на количество реализованных килограмм товара нет, но, разделив 250 на 50, мы легко узнаем, что всего было продано 5 кг. Рассмотрим расчет средней гармонической взвешенной на примере данных таблицы 22.
Таблица 22.
Реализация товара на трех рынках города за II квартал 2012 г.
|
Рынок |
Цена товара за 1 кг, руб. xi |
Выручка от реализации, тыс. руб., Wi = xi * fi |
|
А |
95 |
1900 |
|
Б |
80 |
2800 |
|
В |
90 |
2070 |
Средняя цена любого товара может быть определена только на основе следующего исходного соотношения:
![]()
Общую выручку легко получить простым суммированием выручек по трем рынкам. Данные же о количестве реализованного товара в кг отсутствуют, но их можно узнать, разделив размер выручки от реализации каждого рынка на цену товара. Определим искомую среднюю:
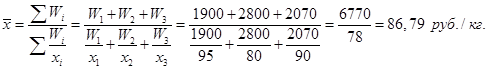
Таким образом, всего было реализовано 78 кг товара, а средняя цена реализации за II квартал 2012 г. составила 86 руб. 79 коп. за 1 кг. В данном случае расчет произведен по формуле средней гармонической взвешенной (23) , где Wi – выручка от реализации, представляющая собой произведение цены товара (хi, руб.) на объем его реализации (fi, кг.)
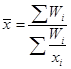 , (23)
, (23)
где
![]() .
.
Средняя геометрическая рассчитывается по формулам:
![]() – невзвешенная (24)
– невзвешенная (24)
![]() – взвешенная (25)
– взвешенная (25)
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста, что будет рассмотрено в соответствующей теме.
Средняя квадратическая. В основе вычислений ряда сводных расчетных показателей лежит средняя квадратическая:
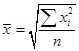 – невзвешенная (26)
– невзвешенная (26)
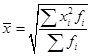 – взвешенная (27)
– взвешенная (27)
Данный вид средней используется при расчете показателей вариации.
Средний уровень моментного ряда динамики рассчитывается по формуле средней хронологической. Для моментного равноотстоящего ряда динамики при расчете среднего уровня используют формулу средней хронологической простой:
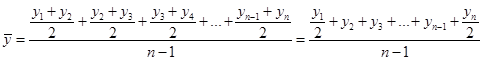 (28)
(28)
или
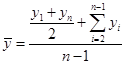
Например, требуется найти среднесписочную месячную численность работников предприятия по данным об их численности на 1-е число каждого месяца в первом квартале 2013 г. (чел.):
|
1/I |
1/II |
1/III |
1/IV |
|
347 |
350 |
349 |
351 |
Это моментный ряд с равноотстоящими уровнями, поэтому среднемесячная численность работников фирмы за первый квартал 2013 года составила:
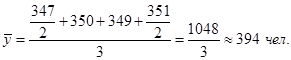
Средний уровень моментных рядов динамики с неравноотстоящими уровнями определяется по формуле средней хронологической взвешенной:
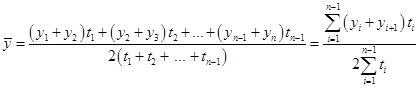 (29)
(29)
где t – продолжительность интервала времени между соседними уровнями.
Например, известна списочная численность рабочих организации на некоторые даты 2012 г. (чел.). Ряд динамики имеет неравноотстоящие уровни во времени:
|
01.01 |
01.03 |
01.06 |
01.09 |
01.01.2013 |
|
530 |
570 |
520 |
430 |
550 |
Среднегодовая численность работников за 2012 г. (по формуле 29) составит:
![]()
Наиболее часто используемыми в экономической практике структурными средними являются мода и медиана.
Мода (Мо) представляет собой значение признака, повторяющееся с наибольшей частотой.
Медианой (Ме) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Рассмотрим определение моды и медианы по несгруппированным данным. Предположим, что 9 торговых фирм города реализуют товар А по следующим оптовым ценам (тыс. руб.).
4,4 4,3 4,4 4,5 4,3 4,3 4,6 4,2 4,6
Так как чаще всего встречается цена 4,3 тыс. руб., то она и будет модальной. Для определения медианы необходимо провести ранжирование:
4,2 4,3 4,3 4,3 4,4 4,4 4,5 4,6 4,6
Центральной в этом ряду является цена 4,4 тыс. руб., следовательно, она и будет медианой. Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений.
В отличие от моды, медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальному закону распределения совокупности. Медиана используется в случаях, когда средняя не позволяет объективно оценить исследуемую совокупность из-за сильного влияния на нее максимальных и минимальных значений. Проиллюстрируем познавательное значение медианы следующим примером.
Допустим, нам необходимо дать характеристику среднего дохода группы людей, насчитывающей 100 человек, из которых 99 имеют доходы в интервале от 30 до 60 тыс. руб. в месяц, а месячные доходы последнего составляют 200 тыс. руб.:
|
№ п.п.
|
1 |
2 |
3 |
… |
50 |
51 |
… |
99 |
100 |
|
Доход, (тыс. руб.) |
30 |
31 |
33 |
… |
42 |
44 |
… |
60 |
200 |
Средняя арифметическая покажет средний доход в 120–140 тыс. руб., который не только значительно меньше дохода сотого человека, но и имеет мало общего с доходами основной части группы. Медиана, равная 43 тыс. руб. (= (42 + 44) : 2), позволит дать объективную характеристику уровня доходов 99 % данной группы людей.
Рассмотрим расчет Мо и Ме по сгруппированным данным (табл. 23).
Таблица 23.
Распределение торговых предприятий города по уровню цен на товар А
|
Цена, руб. (xi) |
Число предприятий, fi |
Накопленные частоты, Si |
|
52 |
12 |
12 |
|
53 |
48 |
60 (= 48 + 12) |
|
54 |
56 |
116 (= 56 + 48 + 12) |
|
55 |
60 |
176 (= 60 + 56 + 48 + 12) |
|
56 |
14 |
190 (= 14 + 60 + 56 + 48 + 12) |
|
Всего |
190 |
- |
В дискретных рядах распределения мода – это значение, имеющее наибольшую частоту. Цену 55 руб. установили максимальное число предприятий (60), следовательно, она является модальной.
Для определения медианы находят номер медианной единицы ряда:
![]() , (30)
, (30)
где n – объем совокупности.
В нашем случае: ![]() .
.
Полученное дробное значение, всегда имеющее место при четном числе единиц совокупности, указывает, что точная середина ряда находится между 95 и 96 предприятиями. Необходимо определить, в какой группе находятся предприятия с этими порядковыми номерами. Это можно сделать, по накопленной частоте Si. Очевидно, что магазинов с этими номерами нет в первой группе, где всего лишь 12 торговых предприятий, нет их и во второй группе (12 + 48 = 60). 95 и 96 предприятия находятся в третьей группе (12 + 48 + 56 = 116) и, следовательно, медианой является цена 54 руб.
Определение моды и медианы по интервальным рядам требует проведения расчетов на основе следующих формул:
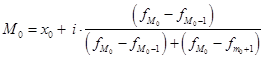 , (31)
, (31)
где
x0 – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
i – ширина модального интервала;
![]() – частота модального интервала;
– частота модального интервала;
![]() – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;
![]() – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
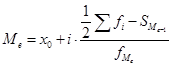 , (32)
, (32)
где
x0 – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);
i – ширина медианного интервала;
![]() – накопленная
частота интервала, предшествующего медианному;
– накопленная
частота интервала, предшествующего медианному;
![]() – частота медианного интервала.
– частота медианного интервала.
Рассчитаем моду и медиану по данным таблицы 24.
Таблица 24.
Распределение населения региона по уровню денежного дохода
|
Среднедушевой денежный доход, руб. |
Удельный вес населения, % |
|
2 400 и менее |
2,4 |
|
2 400–2 500 |
15,4 |
|
2 500–2 600 |
20,1 |
|
2 600–2 700 |
17,2 |
|
2 700–2 800 |
12,8 |
|
2 800–2 900 |
9,2 |
|
2 900–3 000 |
6,5 |
|
3 000–3 100 |
4,5 |
|
3 100–3 200 |
3,2 |
|
3 200–3 300 |
2,3 |
|
свыше 3300 |
6,4 |
|
Всего |
100,0 |
Интервал с границами 2 500–2 600 в данном распределении будет модальным, так как он имеет наибольшую частоту (20,1 %). По формуле (31) определим моду:
![]()
Для определения медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит 1/2 суммы накопленных частот (в нашем случае 50 %):
|
Интервал |
Накопленная частота, % |
|
2 400 и менее |
2,4 |
|
2 400–2 500 |
17,8 |
|
2 500–2 600 |
37,9 |
|
2 600–2 700 |
55,1 |
Медианным является интервал с границами 2 600 – 2 700. Определим медиану по формуле 32:
![]()
Соотношение моды, медианы и средней арифметической
указывает на характер распределения признака в совокупности, позволяет оценить
его асимметрию. Если Мо < Me < ![]() , имеет место правосторонняя асимметрия,
при
, имеет место правосторонняя асимметрия,
при ![]() < Me < Мо следует
сделать вывод о левосторонней асимметрии ряда.
< Me < Мо следует
сделать вывод о левосторонней асимметрии ряда.
На основе полученных в последнем примере значений структурных средних можно заключить, что наиболее распространенным, типичным является среднедушевой доход порядка 2 560 руб. в месяц. В то же время более 1/2 населения располагает доходом свыше 2 670 руб. при среднем уровне 2 735 руб. (средняя арифметическая взвешенная). Из соотношения этих показателей следует вывод о правосторонней асимметрии распределения населения по уровню среднедушевых денежных доходов, что позволяет предполагать достаточную емкость рынка дорогих товаров повышенного качества и товаров престижной группы.
1. Что такое средняя величина и каковы ее основные виды?
2. Что представляет собой исходное соотношение средней величины?
3. В каких случаях применяются взвешенные средние величины? Почему при расчете средней величины важно учитывать веса вариантов показателя?
4. Какими математическими свойствами обладает средняя арифметическая величина?
5. В каких случаях применяется средняя гармоническая величина?
6. Какой вид средних величин используется для расчета среднего значения по моментным рядам динамики?
7. Что такое мода и для чего она применяется?
8. Можно ли рассчитать моду по интервальному ряду распределения?
9. Что характеризует медиана?
10. Можно ли вычислить медиану по ряду распределения, не рассчитывая накопленные частоты?
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Салин В.Н., Чурилова Э.Ю. Практикум по курсу «Статистика» (в системе STATISTICA). – М.: Социальные отношения, 2006.
5. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Задание 1.
Распределение рабочих предприятия по тарифному разряду имеет следующий вид:
|
Тарифный разряд |
1 |
2 |
3 |
4 |
5 |
6 |
|
Число рабочих, чел. |
2 |
5 |
18 |
12 |
9 |
4 |
Определите средний уровень квалификации рабочих предприятия, модальное и медианное значения тарифного разряда.
Задание 2.
По данным о размере месячного товарооборота сети торговых предприятий определите средний размер месячного товарооборота на одно предприятие, модальное и медианное значения товарооборота.
|
Товарооборот в месяц, млн руб. |
Число торговых предприятий |
|
|
|
|
до 10 |
14 |
|
|
|
|
10–20 |
26 |
|
|
|
|
20–30 |
24 |
|
|
|
|
30–40 |
16 |
|
|
|
|
40–50 |
12 |
|
|
|
|
50 и более |
8 |
|
|
|
|
Итого |
100 |
|
|
|
Задание 3.
Производственная деятельность одного из отделений корпорации за месяц характеризуется следующими данными:
|
Предприятие |
Общие затраты на производство, тыс. руб. |
Затраты на 1 руб. произведенной продукции, коп. |
|
1. |
2323,4 |
75 |
|
2. |
8215,9 |
71 |
|
3. |
4420,6 |
73 |
|
4. |
3525,3 |
78 |
Определите средние затраты на 1 руб. произведенной продукции в целом по отделению.
Задание 4.
По данным об остатках оборотных средств предприятия на начало месяца (тыс. руб.) определите среднемесячный размер остатков оборотных средств за 2012 год.
|
01.01.12 |
01.04.12 |
01.07.12 |
01.10.12 |
01.01.13 |
|
200 |
250 |
190 |
210 |
220 |
Цель изучения темы состоит в формировании компетенций о системе показателей, используемых для анализа вариации, особенностях методики их расчета, интерпретации и практическом применении.
В результате успешного освоения темы Вы:
Узнаете:
· почему необходимо изучать вариацию;
· какие показатели вариации существуют и для чего они используются;
· как рассчитываются и интерпретируются показатели вариации;
· какими математическими свойствами обладают показатели вариации и как влияет на их величину изменение всех значений данных или перевод в другую шкалу измерений.
Приобретете компетенции:
· владение методами теоретического и экспериментального исследования;
· понимание роли и значения информации в развитии современного общества и экономических знаний;
· владение основными методами, способами и средствами получения, хранения, переработки информации;
· способность анализировать финансовую отчетность и принимать обоснованные решения;
· способность оценивать эффективность использования различных систем учета и распределения затрат; иметь навыки калькулирования и анализа себестоимости продукции;
· способность обосновывать решения в сфере управления оборотным капиталом;
· умение измерять силу вариации признака при помощи абсолютных и относительных показателей;
· способность рассчитывать показатели вариации и делать выводы по их значениям;
· способность оценивать количественную однородность любого набора данных;
· умение рассчитывать значения показателей вариации при систематическом изменении всех значений исследуемого признака.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· вариация, или изменчивость;
· отклонение от средней;
· размах вариации;
· среднее линейное отклонение;
· дисперсия;
· среднее квадратическое отклонение;
· линейный коэффициент вариации;
· коэффициент вариации.
Вопросы темы:
1. Причины изучения вариации.
2. Показатели вариации и способы их расчета.
3. Математические свойства показателей вариации.
Теоретический материал по теме
Одна из причин, по которой существует необходимость в проведении статистического анализа и постоянном сборе и обновлении информации о социальных и экономических явлениях, состоит в том, что данные изменчивы.
Вариацию (от лат. variatio – «изменение, различие»), или изменчивость, можно определить как степень различия между отдельными значениями признака или показателя.
Почему важно изучать вариацию? В чем ценность информации о том, насколько отличаются значения признака друг от друга?
Ситуация, в которой присутствует изменчивость, всегда связана с долей риска и неопределенностью в будущем. Систематическое воздействие различных факторов и условий вызывает изменение отдельных вариантов признаков или показателя в целом. В большинстве случаев обнаружить такое воздействие и тем самым снизить риск возможно, изучая колебания или индивидуальные различия значений, а не обобщающие величины.
Например, биржевой или финансовый аналитик для прогнозирования игры на бирже или анализа поведения конкретной ценной бумаги извлечет больше полезной информации, изучая колебания курса акции, чем среднюю величину курса этой акции. Менеджера по персоналу при изучении производительности труда работников компании будут больше интересовать причина и размер отклонения количества обработанных за день каждым сотрудником заказов от среднего количества заказов, установленного нормой или рассчитанного для данной категории работников. А по тому, насколько мало или велико среднее отклонение от нормы в разных бригадах (отделах, сменах), менеджер сможет судить об их однородности с точки зрения производительности отдельных сотрудников и принять меры для ее выравнивания и повышения в целом по предприятию.
Показатели изменчивости индивидуальных значений используют для организации контроля качества на производстве, оценки доходности финансовых вложений, сравнительном анализе конкурентных возможностей предприятий, планировании затрат, маркетинговых исследованиях, для построения статистических моделей и во многих других случаях.
Каким образом можно получить количественную оценку степени изменчивости (или колеблемости) признака и сделать вывод о степени различия между отдельными его значениями?
Очевидно, что для оценки различия между значениями необходимо сравнить их друг с другом или с некоей постоянной, или объединяющей все эти значения величиной. Согласно определяющему свойству, такой объединяющей все варианты признака величиной является их средняя – или типичный размер признака.
Несмотря на то, что средняя является условным центром распределения вариантов признака, она не дает представления о том, как отдельные значения группируются вокруг нее, сосредоточены ли они вблизи или значительно удалены от центра (рис. 17).
Таблица 25.
|
Итоги продаж за месяц |
|
|
№ менеджера |
Количество договоров |
|
1 |
9 |
|
2 |
13 |
|
3 |
15 |
|
4 |
19 |
|
5 |
16 |
|
6 |
20 |
|
7 |
32 |
|
8 |
25 |
|
9 |
17 |
|
10 |
14 |
|
Итого |
180 |
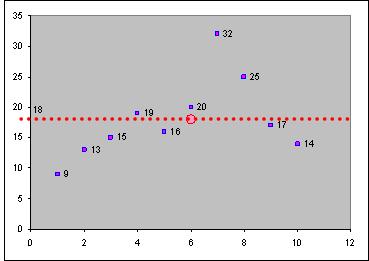
Рис. 17. Количество договоров на сервисное обслуживание, заключенных менеджерами по продажам в течение месяца
Примечание.
На графике по оси Х отмечены N менеджеров, а по оси Y – количество заключенных ими договоров (по данным табл. 25). Очевидно, что среднее количество заключенных договоров на одного менеджера составляет 18. Средний уровень продаж отмечен на графике пунктирной линией. Степень удаленности от средней определяется длинной вертикального отрезка от каждой точки на графике, обозначающей количество заключенных соответствующим менеджером договоров, до пунктирной линии.
Чем ближе расположены значения признака к средней, тем, очевидно, больше их близость по отношению друг к другу и тем выше однородность совокупности в целом.
Для количественной характеристики колеблемости признака необходимо оценить расстояние между каждым индивидуальным значением признака и общей для них средней величиной, которое определяется как разность между их значениями. Эту разность в статистике называют отклонением от средней величины (рис. 18.).
Таблица 26.
|
Итоги продаж за месяц |
||
|
№ менеджера |
Количество договоров |
Отклонение от 18 (от средней величины) |
|
1 |
9 |
–9 |
|
2 |
13 |
–5 |
|
3 |
15 |
–3 |
|
4 |
19 |
1 |
|
5 |
16 |
–2 |
|
6 |
20 |
2 |
|
7 |
32 |
14 |
|
8 |
25 |
7 |
|
9 |
17 |
–1 |
|
10 |
14 |
–4 |
|
Итого |
180 |
0 |
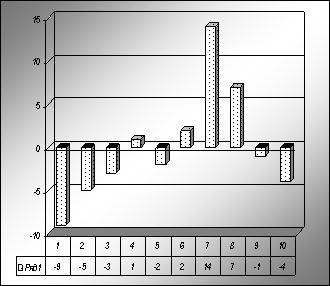
Рис. 18. Гистограмма отклонения количества заключенных договоров каждым менеджером от среднего значения, равного 18
Вычислив среднее из индивидуальных отклонений, мы узнаем величину типичного стандартного расстояния от средней величины.
Найденное число покажет, насколько в среднем отличается каждое значение признака в данной совокупности от средней величины, и будет служить мерой случайности отклонений отдельных значений.
Для количественного измерения степени близости значений отдельных единиц к средней используется система абсолютных и относительных показателей. В общем виде система показателей вариации представлена на рис. 19.

Рис. 19. Основные показатели вариации
Размах вариации – это разность между наибольшим (xmax) и наименьшим (xmin) значениями вариантов.
R = xmax - xmin (33)
Пример 1. Определим показатель размаха вариации по данным табл. 27.
Таблица 27.
Группы предприятий по объему товарооборота
|
Товарооборот, млн. руб. |
Число предприятий fi |
|
90-100 |
28 |
|
100-110 |
48 |
|
110-120 |
20 |
|
120-130 |
4 |
|
ИТОГО |
100 |
R = 130 - 90 = 40 млн. руб.
Размах показывает, что товарооборот предприятий изменяется (колеблется) в пределах от 90 до 130 млн руб., а общая ширина диапазона принимаемых значений (амплитуда колебаний) составляет 40 млн руб.
Размах измеряется в тех же абсолютных единицах, что и значения признака. Размах устанавливает ширину интервала, занимаемого значениями данных, но не отражает отклонений всех вариантов признака в ряду. Поскольку размах зависит только от крайних значений, его величина в большей мере подвержена воздействию случайности, так как в совокупности аномально большие или маленькие значения данных могут быть получены под влиянием случайных причин.
Чтобы дать обобщающую характеристику распределению
отклонений, исчисляют среднее линейное отклонение ![]() ,
которое учитывает различие всех единиц изучаемой совокупности.
,
которое учитывает различие всех единиц изучаемой совокупности.
Среднее линейное отклонение показывает стандартное отличие значения каждого варианта от общей средней величины и определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета их знака (по модулю):
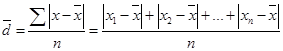 (34)
(34)
Необходимость использования модуля связана со свойством средней арифметической (см. тему 5), согласно которому сумма индивидуальных отклонений от средней арифметической всегда равна нулю. Среднее линейное отклонение измеряется в тех же абсолютных единицах, что и значения признака.
Порядок расчета среднего линейного отклонения:
1) по значениям признака находят среднюю арифметическую;
2)
определяют отклонения каждого
значения xi от средней ![]() ;
;
3)
рассчитывается сумма абсолютных
величин отклонений: ![]() ;
;
4) сумма абсолютных величин отклонений делится на число значений.
Пример 2. Рассчитаем среднее линейное отклонение стажа работников одной смены по данным табл. 28.
Таблица 28.
Стаж работников I смены бригады рабочих на предприятии
|
Таб. номер рабочего |
Стаж работы, лет ( |
|
|
|
А |
1 |
2 |
3 |
|
3 440 |
2 |
- 8 |
8 |
|
3 537 |
3 |
- 7 |
7 |
|
3 825 |
12 |
2 |
2 |
|
2 171 |
15 |
5 |
5 |
|
2 845 |
18 |
8 |
8 |
|
Итого |
50 |
0 |
30 |
Средний стаж работы на одного рабочего смены составляет 10 лет (50 : 5 = 10). Отклонения стажа каждого рабочего от среднего стажа, равного 10 годам, рассчитаны в графе 2, их сумма равна нулю.
Среднее линейное отклонение составляет:
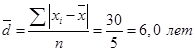 ,
,
т.е. стаж работы каждого работника данной смены в среднем отличается от их среднего значения на 6 лет.
Если данные наблюдения представлены в виде дискретного
или интервального ряда распределения с частотами, ![]() исчисляется
по формуле средней арифметической взвешенной:
исчисляется
по формуле средней арифметической взвешенной:
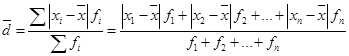 (35)
(35)
Порядок расчета взвешенного среднего линейного отклонения:
1) вычисляется средняя арифметическая взвешенная;
2)
определяются абсолютные отклонения
вариантов от средней ![]() ;
;
3)
полученные отклонения умножаются
на частоты ![]() ;
;
4)
находится сумма взвешенных
отклонений без учета знака:![]() ;
;
5)
сумма взвешенных отклонений
делится на сумму частот: 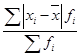 .
.
Для нахождения ![]() по
интервальному ряду распределения вначале находят середины каждого интервала
(как среднюю арифметическую из значений границ) и используют их для расчета
отклонений от общей средней аналогичным образом.
по
интервальному ряду распределения вначале находят середины каждого интервала
(как среднюю арифметическую из значений границ) и используют их для расчета
отклонений от общей средней аналогичным образом.
Пример 3. Рассчитаем среднее линейное отклонение по данным о производительности труда работников одной смены по данным таблицы 29.
Таблица 29.
Производительность труда работников I смены бригады рабочих на предприятии
|
Количество деталей, обрабатываемых 1 рабочим, шт. |
Количество рабочих, чел. |
xi |
xi fi (гр.3 * гр.2) |
|
(гр.5*гр.2) |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
40 - 44 |
2 |
42 |
84 |
5 |
10 |
|
45 - 49 |
1 |
47 |
47 |
0 |
0 |
|
50 - 54 |
2 |
52 |
104 |
5 |
10 |
|
Итого |
5 |
- |
235 |
- |
20 |
Для нахождения средней арифметической вначале были рассчитаны середины каждого интервала и записаны в графу 3. Эти значения показывают, сколько в среднем деталей обрабатывает за смену один работник по каждой группе производительности труда. Данные значения мы обозначаем как Хi и будем использовать для дальнейших расчетов.
Средняя производительность труда одного рабочего данной смены составляет 235 : 5 = 47 деталей:
Индивидуальные отклонения от средней (без учета знака) указаны в графе 5. Взвешенные отклонения – в графе 6, их сумма составляет 20 единиц.
Следовательно:
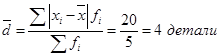 .
.
Это значит, что в среднем каждый работник данной смены обрабатывает за рабочее время на 4 детали меньше или больше, чем средний уровень производительности по смене, составляющий 47 деталей.
Несмотря на то, что среднее линейное отклонение учитывает колеблемость всех значений признака, при его расчете в некотором смысле нарушается элементарное правило математики, так как отклонения от среднего значения суммируются без учета знаков.
Избежать указанного недочета позволяет возведение каждого индивидуального отклонения от средней в квадрат. Рассчитав среднюю величину из возведенных в квадрат отклонений, можно вернуться к исходному порядку данных путем извлечения квадратного корня. Найденное число будет также характеризовать типичное отклонение вариантов признака от средней величины в данной совокупности.
На практике квадратические оценки признаются более состоятельными, поскольку они не нарушают математических правил, а размер погрешности от возведения в квадрат является минимальным. Это объясняется вторым свойством средней арифметической величины (см. тему 5), согласно которому сумма квадратов отклонений от средней всегда меньше, чем аналогичная величина, рассчитанная от любого другого числа.
Основными показателями вариации, для расчета которых используются квадратические оценки, являются дисперсия и среднее квадратическое отклонение.
Дисперсия –
это средняя арифметическая из квадратов отклонений каждого значения признака от
общей средней. Дисперсия обычно называется средним квадратом отклонений и
обозначается ![]() . В зависимости от исходных
данных дисперсия может вычисляться как средняя арифметическая простая или
взвешенная.
. В зависимости от исходных
данных дисперсия может вычисляться как средняя арифметическая простая или
взвешенная.
Если каждый вариант признака повторяется только один раз, используют простую (невзвешенную) формулу:
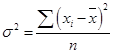 (36)
(36)
Если варианты признака повторяются неодинаковое количество раз, используют взвешенную формулу:
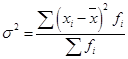 (37)
(37)
Среднее квадратическое отклонение (в литературе также часто используется термин «стандартное
отклонение») представляет собой квадратный корень из дисперсии и обозначается ![]() .
.
Формулы для его расчета следующие:
· среднее квадратическое отклонение невзвешенное:
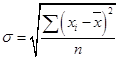 (38)
(38)
· среднее квадратическое отклонение взвешенное:
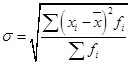 (39)
(39)
Математические преобразования формул (38) и (39) приводят к упрощенному виду формулы, которая часто оказывается более удобной на практике, особенно при расчете s по несгруппированным данным:
![]() , (40)
, (40)
где
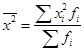 (41)
(41)
Среднее квадратическое отклонение является обобщающей характеристикой абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.) и показывает, насколько в среднем отличается значение каждого варианта признака от среднего значения для данной совокупности.
Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Между ними имеется соотношение:
![]() (42)
(42)
Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.
Для вычисления среднего квадратического отклонения необходимо рассчитать дисперсию.
Порядок расчета дисперсии по взвешенной формуле:
1) определяют среднюю арифметическую взвешенную;
2)
рассчитывают отклонения вариантов
от средней:![]() ;
;
3)
возводят в квадрат отклонение
каждого варианта от средней: ![]() ;
;
4)
умножают квадраты отклонений на
веса (частоты): ![]() ;
;
5)
суммируют полученные произведения:
![]() ;
;
6)
полученную сумму делят на сумму
весов: 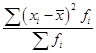 .
.
Пример 4. Найдем дисперсию и среднее квадратическое отклонение по данным о размере квартальной премии сотрудников одного из отдела фирмы (табл. 30).
Таблица 30.
Размер квартальной премии сотрудников отдела обслуживания фирмы
|
Премия, тыс. руб. (xi) |
Число сотрудников, fi |
xi fi |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
8 |
7 |
56 |
-2 |
4 |
28 |
|
9 |
10 |
90 |
-1 |
1 |
10 |
|
10 |
15 |
150 |
0 |
0 |
0 |
|
11 |
12 |
132 |
1 |
1 |
12 |
|
12 |
6 |
72 |
2 |
4 |
24 |
|
ИТОГО |
50 |
500 |
0 |
- |
74 |
Исчислим среднюю арифметическую взвешенную:
500 : 50 = 10 тыс. руб.
Значения отклонений от средней и их квадратов представлены в таблице 30 в графах 4 и 5.
Определим дисперсию: 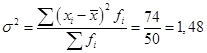 .
.
Среднее квадратическое отклонение будет равно:
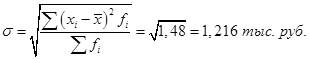
Это значит, что размер премии каждого сотрудника отдела обслуживания отличается от среднеквартальной величины премии по отделу, равной 10 тыс. руб., на 1 216 руб.
Если исходные данные представлены в виде интервального ряда распределения, то сначала надо определить средины каждого интервала, и далее рассчитывать показатели вариации аналогичным образом.
Пример 5. Рассчитаем дисперсию и среднее квадратическое отклонение по данным о распределении ценных бумаг по уровню доходности (табл. 31).
Таблица 31.
Распределение ценных бумаг по уровню доходности, %
|
Доходность 1 ценной бумаги, % |
Количество ценных бумаг, fi |
xi |
xifi |
|
|
|
|
14–16 |
100 |
15 |
1500 |
-3,4 |
11,56 |
1156 |
|
16–18 |
300 |
17 |
5100 |
-1,4 |
1,96 |
588 |
|
18–20 |
400 |
19 |
7600 |
0,6 |
0,36 |
144 |
|
20–22 |
200 |
21 |
4200 |
2,6 |
6,76 |
1352 |
|
ИТОГО |
1000 |
- |
18400 |
|
|
3240 |
Средняя доходность одной ценной бумаги равна:
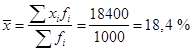
Исчислим дисперсию: 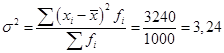 .
.
Среднее квадратическое отклонение составит: ![]() .
.
Следовательно, с каждой ценной бумаги владелец может получить в среднем на 1,8 % больше или меньше, чем величина средней доходности – 18,4 %.
Для характеристики меры вариации изучаемого признака исчисляются показатели в относительных величинах. Они позволяют сравнивать характер вариации признака в разных совокупностях. Относительные показатели вариации рассчитывают как отношение типичного отклонения к средней величине, умножаемое на 100 %.
Линейный коэффициент вариации характеризует долю среднего линейного отклонения от общего размера средней величины и рассчитывается по формуле:
![]() (43)
(43)
Коэффициент вариации рассчитывается как отношение среднего квадратического отклонения к средней величине:
![]() (44)
(44)
Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем, используемым для оценки типичности средних величин. Если V больше 40 %, то это говорит о большой колеблемости признака в изучаемой совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33,3 %.
Пример 6. По данным таблицы 31 рассчитаем коэффициент вариации.
![]()
Это означает, что ценные бумаги однородны по проценту доходности (т.к. V = 9,78 % < 33 %).
Следует отметить, что коэффициент вариации может быть более 100 %, что бывает при наличии значений, сильно отличающихся от средней величины, например, отрицательных значений или аномально больших или малых значений отдельных вариантов. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине и для более качественного ее исследования необходимо разбить ее на более однородные части или с помощью специальных методов исключить влияние на среднюю аномальных вариантов.
На практике часто возникают ситуации, которые системно оказывают влияние на все значения исследуемого признака. Например, при системном сокращении или повышении расценок, переходе к использованию для расчетов условных единиц, переходе с одной валюты на другую (с доллара США к евро или фунтам стерлингов), при изменении шкалы измерений. Такие изменения отражаются в систематическом увеличении или уменьшении каждого значения показателя на некоторые фиксированные величины или в несколько раз. При таких изменениях необходимости в перерасчете всех показателей вариации не возникает, так как они обладают рядом математических свойств, зная которые, можно легко определить их величину по совокупности обновленных данных. Рассмотрим основные свойства на примере данных о затратах на производство единицы продукции трех отделений корпорации, каждое из которых в среднем ежемесячно производит 2 тыс. единиц продукции (табл. 32).
Таблица 32.
Затраты на производство единицы продукции по корпорации
|
Отделение корпорации |
Затраты на единицу продукции, руб. (Хi) |
Средний объем производства, единиц продукции в месяц |
|
А |
1 |
2 |
|
1 отделение |
10 |
2 000 |
|
2 отделение |
12 |
2 000 |
|
3 отделение |
14 |
2 000 |
|
Итого |
- |
6 000 |
Так как каждое отделение производит одинаковое количество продукции, для расчета обобщающих показателей – средней, дисперсии, среднего квадратического отклонения – можно воспользоваться невзвешенной формулой. Промежуточные расчеты показателей представлены в таблице 33.
Таблица 33.
Затраты на производство единицы продукции по корпорации
|
№ отделения |
Хi |
|
|
|
А |
1 |
2 |
3 |
|
1 отделение |
10 |
- 2 |
4 |
|
2 отделение |
12 |
0 |
0 |
|
3 отделение |
14 |
+ 2 |
4 |
|
Итого |
36 |
0 |
8 |
|
|
|
|
|
|
|
|
|
Средние затраты на единицу продукции корпорации составляют 12 руб. Риск превышения затрат на единицу продукции составляет 1,632 руб. – величину среднего квадратического отклонения. Общие производственные затраты в месяц составляют в среднем:
12 * 6000 = 72 000 руб.
Свойство 1. Уменьшение или увеличение всех значений признака на одинаковую величину не меняет величины дисперсии, среднего квадратического отклонения и размаха вариации.
![]() (45)
(45)
Проверим, как повлияет на величину показателей вариации снижение затрат на единицу продукции на 2 руб. в результате оптимизации производственных процессов при неизменном объеме производства (табл. 34).
Таблица 34.
Затраты на производство единицы продукции по корпорации
|
№ отделения |
(Хi - 2) |
(Хi - 2) - |
((Хi - 2) - |
|
А |
1 |
2 |
3 |
|
1 |
8 |
- 2 |
4 |
|
2 |
10 |
0 |
0 |
|
3 |
12 |
+ 2 |
4 |
|
Итого |
30 |
0 |
8 |
|
|
|
|
|
|
Как мы видим, при снижении затрат на производство единицы продукции на 2 руб. риск превышения затрат на единицу продукции остался неизменным – 1,63 руб., также как и величины дисперсии, и размаха вариации. Но это не означает, что корпорации не нужно оптимизировать производство: за счет снижения затрат на единицу общие производственные затраты корпорации составили: 10 * 6000 = 60 000 руб., что на 12 тыс. руб. (или на 16,6 %) меньше, чем было до оптимизации – 72 000 руб.
Свойство 2. Увеличение всех значений признака в k раз (k – любое число) увеличивает дисперсию в k2 раз, среднее квадратическое отклонение и размах – в k раз. (Если k<0, то коэффициент берется по модулю). Коэффициент вариации при этом не меняется.
![]() (46)
(46)
Предположим условную ситуацию, что все затраты на единицу продукции в результате двойного удорожания цен на сырье выросли в два раза. Как это (при неизменном объеме производства) отразится на риске увеличения затрат на единицу продукции по сравнению с исходным уровнем (по данным табл. 32)? Проверим расчеты (табл. 35).
Таблица 35.
Затраты на производство единицы продукции по корпорации
|
№ отделения |
(Хi * 2) |
(Хi * 2) – |
((Хi * 2)
– |
|
А |
1 |
2 |
3 |
|
1 |
20 |
–4 |
16 |
|
2 |
24 |
0 |
0 |
|
3 |
28 |
+4 |
16 |
|
Итого |
72 |
0 |
32 |
|
|
|
|
|
|
|
|
|
Как мы видим, при увеличении затрат на производство единицы продукции в 2 раза размах вариации вырос в 2 раза. Риск превышения затрат на единицу продукции составляет 3,266 руб., т.е. также в два раза больше, чем первоначальный 1,632 руб. (3,266 : 1,632 = 2). Соответственно, для получения оценки риска от увеличения затрат на единицу продукции в два раза достаточно исходное среднее квадратическое отклонение 1,632 умножить на 2.
Размер дисперсии составил 10,6667. Это в 4 раза больше, т.е. в 22 раз, чем исходное значение (10,6667 : 2,6667 = 3,9999 ≈ 4 (из-за округлений)).
Коэффициент вариации остался неизменным – 13,6 %, как и до двукратного увеличения затрат на единицу произведенной продукции.
Свойство 3. Дисперсия
отклонений значений признака от произвольного числа А (Xi – А)2
увеличивает дисперсию отклонений от средней ![]() на
число, равное возведенной в квадрат разнице между средней и этим числом А, т.е.
на
на
число, равное возведенной в квадрат разнице между средней и этим числом А, т.е.
на ![]() .
.
![]() (47)
(47)
Для иллюстрации свойства предположим, что руководство корпорации решило оценить уровень риска при условии, что средние затраты на единицу продукции в корпорации остались бы на уровне прошлого года – 15 руб. Проверим действие свойства, рассчитав отклонения затрат на единицу продукции от 15 (табл. 36).
Таблица 36.
Затраты на производство единицы продукции по корпорации
|
№ отделения |
Хi |
Хi - 15 |
(Хi - 15)2 |
|
А |
1 |
2 |
3 |
|
1 отделение |
10 |
-5 |
25 |
|
2 отделение |
12 |
-3 |
9 |
|
3 отделение |
14 |
-1 |
1 |
|
Итого |
36 |
0 |
35 |
![]() ,
,
где
![]() .
.
Свойство подтверждено:
11,6667 - 2,6667 = 9 = (12 - 15)2 = (-3)2
1. Что такое изменчивость, или вариация данных?
2. Какой показатель и почему используют для оценки изменчивости?
3. Что характеризует среднее квадратическое отклонение? В каких единицах оно измеряется?
4. В каких случаях для расчета показателей вариации используются взвешенные формулы?
5. Для чего применяется коэффициент вариации? В каких единицах он измеряется?
6. Как изменится дисперсия, если все значения признака увеличить на 100?
7. Как отразится на величине коэффициента вариации сокращение каждого значения признака в 4 раза?
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Салин В.Н., Чурилова Э.Ю. Практикум по курсу «Статистика» (в системе STATISTICA). – М.: Социальные отношения, 2006.
5. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Задание 1.
По данным о ценах на финансовый актив нескольких компаний-конкурентов определите, является ли предлагаемая вашей компанией цена 24 тыс. руб. конкурентоспособной относительно цен конкурентов. Является ли отличие цены вашей компании от цен конкурентов типичным? Следует ли вашей компании каким-либо образом изменить установленную цену, если компания придерживается стратегии ценовой консолидации с конкурентами? Каким будет среднеквадратическое отклонение цены актива по всем конкурентам, если все компании решат увеличить первоначальную цену актива на 20 %?
|
№ компании |
Цена актива, тыс. руб. |
|
|
|
|
1 |
29 |
|
|
|
|
2 |
31 |
|
|
|
|
3 |
35 |
|
|
|
|
4 |
29 |
|
|
|
|
5 |
35 |
|
|
|
|
6 |
27 |
|
|
|
|
7 |
38 |
|
|
|
|
8 |
24 |
|
|
|
|
9 |
34 |
|
|
|
|
10 |
38 |
|
|
|
|
Итого |
|
|
|
|
Задание 2.
Оцените однородность распределения строительных фирм по объему инвестиций по следующим данным:
|
Объем инвестиций, млн руб. |
Число фирм |
|
|
|
|
|
|
6–8 |
4 |
|
|
|
|
|
|
8–10 |
6 |
|
|
|
|
|
|
10–12 |
32 |
|
|
|
|
|
|
12–14 |
34 |
|
|
|
|
|
|
14–16 |
27 |
|
|
|
|
|
|
16–18 |
10 |
|
|
|
|
|
|
18–20 |
7 |
|
|
|
|
|
|
Итого: |
120 |
|
|
|
|
|
Задание 3.
Средний квадрат отклонений индивидуальных значений признака от их средней величины равен 100, а средняя величина – 15. Определите, чему равен средний квадрат отклонений индивидуальных значений признака от величины, равной 10 и 25.
Цель изучения темы состоит в формировании системы знаний и компетенций о видах выборочного наблюдения, применяемого в статистических исследованиях, его преимуществах, основных показателях и способах их расчета.
В результате успешного освоения темы Вы:
Узнаете:
· какие виды выборочного наблюдения существуют и для чего они применяются;
· основные задачи выборочного наблюдения и преимущества его применения;
· какими показателями характеризуются результаты выборочного наблюдения;
· что такое средняя и предельная ошибка выборки и каковы особенности их расчета для выборок различных видов.
Приобретете компетенции:
· владение методами количественного анализа и моделирования, теоретического и экспериментального исследования;
· понимание роли и значения информации в развитии современного общества и экономических знаний;
· владение основными методами, способами и средствами получения, хранения, переработки информации;
· способность анализировать финансовую отчетность и принимать обоснованные решения;
· умение применять количественные и качественные методы анализа при принятии управленческих решений и строить экономические, финансовые и организационно-управленческие модели;
· умение определять вид выборки и рассчитывать ее необходимый объем;
· способность распространять результаты выборочного наблюдения на генеральную совокупность и формулировать выводы по полученным результатам.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· выборочное наблюдение;
· генеральная и выборочная совокупность;
· повторный и бесповторный отбор;
· собственно случайная выборка, таблица случайных чисел;
· механическая (систематическая) выборка;
· стратифицированная случайная выборка;
· средняя ошибка выборки;
· предельная ошибка выборки.
Вопросы темы:
1. Теоретические основы выборочного наблюдения.
2. Виды выборочного наблюдения. Способы и методы отбора единиц в выборочную совокупность.
3. Средняя и предельная ошибка выборки. Построение доверительных границ для среднего и доли.
4. Определение объема выборочной совокупности.
Теоретический материал по теме
Выборочным наблюдением называется такое несплошное обследование, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность. Полученные статистические характеристики сопровождаются указанием на точность оценивания, которая зависит от репрезентативности (представительности) выбранной совокупности, т.е. от того, насколько качественно она отражает закономерность генеральной совокупности.
Генеральной совокупностью (основой выборки) называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Количество единиц генеральной совокупности обозначается через N.
Выборочная совокупность – это небольшой набор объектов, извлеченных из генеральной совокупности по определенным правилам. Количество единиц выборочной совокупности обозначается через n.
Доля выборочных единиц в объеме генеральной совокупности, выраженная в процентах, называется долей отбора (процентом выборки) и определяется следующим образом:
![]() (48)
(48)
Например, при объеме генеральной совокупности в 2 000 единиц и выборочной в 500 единиц, говорят о 25-процентной выборке.
Единицами отбора называют элементы отбора при формировании выборочной совокупности. Единицей наблюдения выступает объект, признаки которого подлежат регистрации. Единица наблюдения может не совпадать с единицей отбора.
Если исследуется количественный признак, то
непосредственной задачей выборочного наблюдения выступает оценка среднего и
суммарного значений. Генеральное среднее значение определяется по данным
генеральной совокупности и обозначается через ![]() .
Формула для его расчета имеет вид:
.
Формула для его расчета имеет вид:
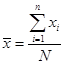 (49)
(49)
Выборочное среднее (![]() )
является оценкой генерального среднего и определяется по формуле:
)
является оценкой генерального среднего и определяется по формуле:
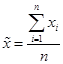 (50)
(50)
Генеральная дисперсия единиц количественного признака определяется по формуле:
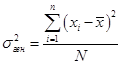 (51)
(51)
Так как генеральная дисперсия по большей части в ходе исследования остается неизвестной, то условно ее принимают равной дисперсии, рассчитываемой по выборочным данным:
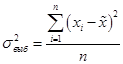 (52)
(52)
При малочисленных выборках (менее 30 объектов) в формулу необходимо внести поправку – уменьшить знаменатель на единицу:
![]() (53)
(53)
Помимо определения характеристик количественных признаков можно произвести оценку характеристик альтернативных показателей. Численность единиц, обладающих изучаемыми признаками в генеральной совокупности, обозначается через M, а в выборочной – через m. Тогда доля единиц, обладающих исследуемыми признаками в генеральной совокупности, определяется как:
![]() , (54)
, (54)
где
М – численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака.
В выборочной совокупности:
![]() , (55)
, (55)
где
m – численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака.
Генеральная дисперсия доли альтернативного признака рассчитывается по формуле:
![]() , (56)
, (56)
где
p – генеральная доля, то есть доля единиц, обладающих определенным вариантом или вариантами изучаемого признака во всей генеральной совокупности;
q – доля единиц, не обладающих исследуемым признаком (q = 1 – p).
Выборочная дисперсия доли:
![]() , (57)
, (57)
где
w – выборочная доля, то есть доля единиц, обладающих определенным вариантом или вариантами изучаемого признака в выборочной совокупности.
Основные преимущества выборочного метода по сравнению со сплошным заключаются в следующем:
1. Быстрота получения результатов обследования за счет снижения объема наблюдаемой совокупности из-за отбора и обработки данных только по определенной части ее единиц.
2. Значительное снижение стоимости наблюдения.
3. Возможность лучшей организации проведения обследования за счет минимизации влияния ошибок регистрации в силу меньшего количества обследуемых единиц генеральной совокупности.
4. Возможность расширения программы наблюдения в силу снижения численности наблюдаемых единиц и возможности включения в программу исследования более широкого круга регистрируемых признаков.
5. Возможность использования в случаях, когда проведение сплошного наблюдения методологически невозможно. Например, при статистическом исследовании качества продукции выборочное наблюдение становится единственно возможным, так как данные виды исследования связаны с порчей или уничтожением продукции. Если генеральная совокупность объектов изучения бесконечно велика и нет возможности обследовать каждую единицу, также используется выборочный метод наблюдения (например, маркетинговые обследования покупателей, изучение пассажиропотоков и т.п.).
Наиболее существенным недостатком выборочного наблюдения является наличие ошибок репрезентативности – ситуаций, при которых выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Это может быть вызвано наличием как случайных, так и систематических ошибок репрезентативности, связанных с нарушением принципов формирования выборочной совокупности.
Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность.
В зависимости от состава и структуры генеральной совокупности различают виды выборок и способы отбора единиц.
Способ отбора единиц в выборочную совокупность может быть повторным или бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения. Число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется.
На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности неизвестен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков. Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Так, например, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.
При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.
Различают следующие методы отбора единиц из генеральной совокупности:
· метод индивидуального отбора, при котором в выборочную совокупность извлекаются отдельные единицы генеральной совокупности, например: при обследовании коммерческих банков – банки, при обследовании населения – конкретные люди и т.д. Применяется при организации собственно случайной, механической и типической выборок;
· метод группового отбора предполагает извлечение единиц из генеральной совокупности группами, например, бригадами, микрорайонами и т.д. Такой отбор применяется при серийной выборке;
· метод комбинированного отбора, при котором вначале отбираются группы единиц, а затем из них случайным образом извлекаются конкретные единицы совокупности.
Каждый метод отбора может быть реализован как повторным, так и бесповторным способами.
Выбор вида выборок определяется задачами исследования и, прежде всего, полнотой и особенностями информации, которой располагает исследователь об объекте наблюдения. Наиболее распространенными видами выборок, применяемыми на практике, являются:
· собственно случайная выборка;
· механическая (систематическая) выборка;
· типическая (стратифицированная, расслоенная) выборка.
Собственно случайная выборка заключается в отборе единиц из генеральной совокупности в целом, без разделения ее на группы, подгруппы или серии отдельных единиц. При этом единицы отбираются в случайном порядке, не зависящем ни от последовательности расположения единиц в совокупности, ни от значений их признаков. Простая случайная выборка строится исходя из следующих правил:
1) каждый объект генеральной совокупности имеет одинаковую вероятность быть отобранным;
2) объекты отбираются независимо друг от друга.
Одним из способов извлечения случайной выборки является применение таблицы случайных чисел для получения номера каждого отобранного объекта генеральной совокупности. Сам объект затем находят в основе выборки. Таблица случайных чисел представляет собой организованную в виде таблицы последовательность чисел, в которой каждая из цифр от 0 до 9 встречается независимо друг от друга с вероятностью 1/10. Составить таблицы случайных чисел можно, например, с помощью датчика случайных чисел. Его содержат все современные статистические пакеты, а также MS Excel («Вставка функций» – «Математические» – «Случайное число»). Для проведения отбора могут быть использованы цифры любого столбца данной таблицы, при этом необходимо учитывать объем генеральной совокупности.
Для получения механической (систематической) выборки необходимо выбрать в основе выборки одну случайную начальную точку (за счет этого вносится в выборку элемент случайности) и затем производить отбор элементов в основе выборки с некоторым постоянным шагом. При таком способе отбора генеральная совокупность делится на столько групп, сколько единиц наблюдения должно войти в выборку, и из каждой группы отбирается одна единица. Единицы генеральной совокупности нумеруются числами от 1 до N, после чего отбираются каждые N/n-е объекты для выборки, находящиеся на равном расстоянии друг от друга (n – объем выборки, N – объем генеральной совокупности).
Величина N/n называется шагом, или интервалом отбора между выбираемыми элементами. Например, если для 1000 единиц требуется создать 5-процентную выборочную совокупность, то объем выборки будет 50 единиц, интервал отбора составит 1000 / 50 = 20. Это значит, что в выборку попадет каждый 20-й элемент генеральной совокупности.
Существуют два способа формирования основы механической выборки: по неранжированным (по отношению к изучаемым признакам) данным и по ранжированной генеральной совокупности.
В первом случае результаты механического отбора будут являться реализацией случайного бесповторного отбора, так как единицы наблюдения располагаются в случайном порядке. Усилить данную случайность возможно выбором начальной точки отсчета случайным образом из интервала, соответствующего первому шагу отбора.
Во втором случае единицы наблюдения определенным образом упорядочиваются по величине изучаемого признака и отбор осуществляется в соответствии с его шагом N/n, начиная с единицы, являющейся серединой первого интервала.
Однако метод систематического отбора имеет серьезные недостатки из-за невозможности оценить точность получаемой выборки. Недопустимо использование систематической выборки в случае повторяемости некоторого ее фрагмента, который по размеру соответствует и интервалу отбора. Например, если во время упаковки на конвейере каждому 20-му изделию уделяют особое внимание и по воле случая при шаге выборки № 20 вы отберете в свою систематическую выборку именно эти изделия, то результаты систематической выборки будут полностью бесполезны в отношении репрезентативности качества других обычных изделий.
Стратифицированную случайную выборку применяют, когда генеральная совокупность содержит ясные, известные, легко идентифицированные группы. Такие группы также называются слоями (стратами), в связи с чем типический отбор называют также стратифицированным, или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.
Стратифицированную выборку получают путем осуществления случайной выборки отдельно в каждой страте генеральной совокупности. Существуют следующие два вида организации отбора внутри типической группы:
· пропорционально объему типических групп;
· пропорционально степени колеблемости значений признака у единиц наблюдения в группах.
При проведении отбора пропорционально объему типических групп число единиц, подлежащих отбору из каждой группы, определяется следующим образом:
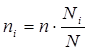 , (58)
, (58)
где
ni – количество извлекаемых единиц для выборки из i-й типической группы;
n – общий объем выборки;
Ni – количество единиц генеральной совокупности, составивших i-ю типическую группу;
N – общее количество единиц генеральной совокупности.
Размеры выборки для каждой из страт могут быть разными. Для одних страт процесс отбора может быть сложнее и дороже, чем для других, и для этих страт используются меньшие по размеру выборки. Другие страты могут иметь большую изменчивость, и поэтому для них требуется использовать большие по размеру выборки. Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым.
Из одной и той же генеральной совокупности объемом N единиц можно извлечь множество различных выборок заданного объема n. Тогда в каждом случае рассчитанные отклонения выборочных характеристик от генеральных будут различны. Если определить среднюю из ошибок всех возможных выборок заданного объема, то получим их обобщающую характеристику – среднюю ошибку выборки (μ), которая показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной.
Ошибка выборки, или отклонение выборочной средней от средней генеральной, находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности и в обратной зависимости – от объема выборки. Таким образом, среднюю ошибку выборки можно представить как
![]() (59)
(59)
При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующая зависимость:
![]() (60)
(60)
В связи с тем, что на практике в большинстве случаев
из генеральной совокупности в определенный момент времени производится только
одна выборка, дисперсия изучаемого признака по этой выборке и используется при
расчете ошибки. При достаточно большом объеме выборки отношение ![]() близко к 1.
близко к 1.
При бесповторном отборе необходимо учитывать поправку
на конечность совокупности ![]() .
.
При стратифицированной выборке в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, поэтому при типизации генеральной совокупности исключается влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.
Формулы для определения средней ошибки выборки индивидуальны для различных способов отбора (повторного и бесповторного), видов используемых выборок и оцениваемых статистических показателей (таблица 37).
Таблица 37.
Формулы для расчета средней ошибки выборки (μ)
|
|
Способ отбора |
|
|
повторный |
бесповторный |
|
|
Вид выборки |
Собственно случайная выборка |
|
|
При оценке среднего |
|
|
|
При оценке доли |
|
|
|
При оценке суммарного значения признака |
|
|
|
Вид выборки |
Систематическая (механическая) выборка |
|
|
При оценке среднего |
- |
|
|
При оценке доли |
- |
|
|
При оценке суммарного значения признака |
- |
|
|
Вид выборки |
Стратифицированная (типическая) выборка |
|
|
При оценке среднего |
|
|
|
При оценке доли |
|
|
|
При оценке суммарного значения признака |
|
|
|
где w (1 – w) – выборочная дисперсия доли;
|
||
Для определения возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки (Δ), которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы:
![]() (61)
(61)
Уровень предельной ошибки выборки зависит от следующих факторов:
· от степени вариации единиц генеральной совокупности;
· от объема выборки;
· от выбранных схем отбора – повторного и бесповторного;
· от уровня доверительной вероятности.
Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки при достаточно большом объеме выборочной совокупности подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.
Значения интеграла Лапласа при различных величинах t табулированы и представлены в статистических справочниках. Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше – по таблице распределения Стьюдента. При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:
|
Значение доверительной вероятности P |
0,6827 |
0,8664 |
0,9545 |
0,9973 |
|
Значение коэффициента доверия t |
1,000 |
1,500 |
2,000 |
3,000 |
Например, если при расчете предельной ошибки выборки мы используем значение t = 2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки.
Построение доверительных интервалов для генеральной средней и доли осуществляется следующим образом:
![]() (62)
(62)
Определение границ генеральной средней и доли состоит из следующих этапов:
· нахождение выборочного значения средней (или доли);
· определение средней ошибки выборки в соответствии с выбранной схемой отбора и видом выборки;
· задание доверительной вероятности Р и определение коэффициента доверия t;
·
вычисление предельной ошибки
выборки ![]() ;
;
· построение доверительного интервала для среднего (доли).
Пример 1. Для изучения среднего размера расходов на стоматологическую страховку, которую готовы заплатить служащие банка в год, из 1350 банковских работников было обследовано 810 человек методом случайного повторного отбора. В результате были получены следующие данные (таблица 38).
Таблица 38.
Результаты выборочного обследования банковских служащих на предмет размера расходов на стоматологическую страховку
|
Размер страховки, дол. |
до 250 |
250–500 |
500–750 |
750–1000 |
1000–1250 |
1250–1500 |
|
|
Количество человек |
80 |
105 |
134 |
231 |
169 |
91 |
810 |
Определите с вероятностью 0,954:
а) предельную ошибку выборки и границы для генеральной средней;
б) в каких границах находится генеральная доля банковских служащих, готовых израсходовать на страховку не более 1000 долл.
Решение:
1. По результатам выборочного обследования рассчитаем среднее значение и дисперсию выборочной совокупности, для чего необходимо рассчитать середины интервалов группировочного признака «размер расходов» (табл. 38). Для удобства расчетов построим вспомогательную таблицу 39.
Таблица 39.
Вспомогательная таблица для расчета среднего размера страховки и дисперсии
|
Размер страховки, долл. xi |
Количество человек fi |
Середина интервала,
|
|
|
|
до 250 |
80 |
125 |
10 000 |
1 250 000 |
|
250–500 |
105 |
375 |
39 375 |
14 765 625 |
|
500–750 |
134 |
625 |
83 750 |
52 343 750 |
|
750–1000 |
231 |
875 |
202 125 |
176 859 375 |
|
1 000–1 250 |
169 |
1125 |
190 125 |
213 890 625 |
|
1 250–1 500 |
91 |
1375 |
125 125 |
172 046 875 |
|
Итого: |
810 |
- |
650 500 |
631 156 250 |
Выборочная средняя составит: ![]() долл.
долл.
Выборочная дисперсия изучаемого признака:
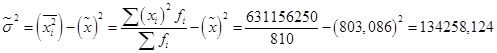
Выборочное среднеквадратическое отклонение составит: ![]() долл.
долл.
2. Определим среднюю ошибку повторной случайной выборки: ![]() .
.
3. Определим предельную ошибку выборки с заданной вероятностью. Для этого по таблице значений вероятности функции нормального распределения находим величину коэффициента доверия t, соответствующего вероятности 0,954. При F(t) = 0,954, t = 2.
Предельная ошибка выборки с вероятностью 0,954 равна: ![]() .
.
Найдем доверительные границы для среднего значения размера страховки:
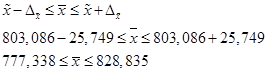
Таким образом, в 954 случаях из 1000 средний объем денежных средств, которые служащие готовы потратить на стоматологическую страховку в год, не будет превышать 828,8 долл. и не будет меньшим, чем 777,3 долл.
Теперь определим, в каких границах в генеральной совокупности находится доля банковских служащих, готовых израсходовать на страховку не более 1000 долл.
4. Рассчитаем выборочную долю. Количество банковских работников, готовых потратить на страховку не более 1000 долл., в выборочной совокупности составляет 550 ед., следовательно: m = 550, n = 810, w = m / n= 550 / 810 = 0,679.
5. Рассчитаем выборочную дисперсию доли:
![]()
6. Средняя ошибка выборки при использовании повторной
схемы отбора составит: ![]() .
.
Предположим, что была использована бесповторная схема отбора. Тогда средняя ошибка выборки с учетом поправки на конечность совокупности составит:
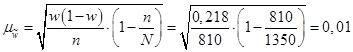
7. Определим предельную ошибку выборки. При значении вероятности р = 0,954 по таблице нормального распределения получаем значение коэффициента доверия t = 2.
![]()
8. Определим границы для генеральной доли с вероятностью 95,4 % для бесповторного отбора:
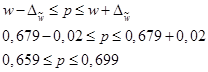
Следовательно, с вероятностью 0,954 можно утверждать, что в генеральной совокупности доля сотрудников, готовых израсходовать на стоматологическую страховку не более 1 000 долл. в год, не меньше 65,9 % и не больше 69,9 %.
Пример 2. Руководство регионально-распределенной корпорации дало поручение провести исследование частоты обращения сотрудников к недавно введенной в эксплуатацию корпоративной базе знаний, содержащей сведения об истории реализации корпорацией проектов, инструкции по действию и ответы на вопросы о действиях сотрудника в сложных производственных ситуациях, экспресс-курсы повышения квалификации и другую справочную информацию. Для этих целей была использована 15 % бесповторная типическая выборка, типические группы которой соответствуют региональному отделению. При отборе, пропорциональному объему типических групп, получены данные (таблица 40).
Таблица 40.
Результаты обследования сотрудников корпорации
|
Региональное отделение |
Всего сотрудников, чел. Ni |
Обследовано в результате выборочного наблюдения, чел., ni |
Среднее число обращений одного сотрудника к корпоративной базе знаний за полгода, |
Внутригрупповая выборочная дисперсия, |
|
А |
650 |
98 |
11 |
9 |
|
Б |
610 |
92 |
8 |
15 |
|
В |
580 |
87 |
5 |
18 |
|
Г |
360 |
54 |
6 |
24 |
|
Д |
350 |
52 |
10 |
12 |
|
Итого: |
2550 |
383 |
- |
- |
Общий объем выборочной совокупности составит:
![]()
Количество сотрудников, которое необходимо обследовать в каждом региональном отделении, определим согласно формуле:
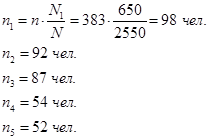
1. Выборочная средняя, основываясь на значениях средних типических групп, составит:
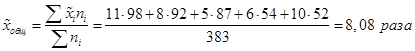
2. Средняя из внутригрупповых дисперсий равна:
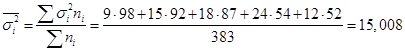
3. Средняя ошибка выборки:
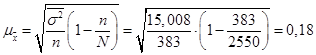
С вероятностью 0,954 находим предельную ошибку выборки:
![]()
4. Доверительные границы для среднего находятся в пределах:
![]()
![]()
Важным вопросом, особенно на этапе проектирования выборочного наблюдения, является определение объема выборочной совокупности.
Чем больше объем выборки, тем меньше значения средней и предельной ошибок выборочного наблюдения и, следовательно, тем уже границы генеральной средней и генеральной доли. В то же время необходимо учитывать, что большой объем выборки приводит к удорожанию обследования, увеличению сроков сбора и обработки материалов, требует привлечения дополнительного персонала и соответствующего материально-технического обеспечения. Затраты всех ресурсов на 20–30 %-ное выборочное наблюдение уже сопоставимы с расходами на сплошное обследование. При этом не следует забывать, что статистические характеристики, полученные по выборочной совокупности, всегда имеют вероятностную основу и всегда будут уступать результатам сплошного наблюдения по точности и надежности. Поэтому при подготовке выборочного наблюдения необходимо определить тот минимально необходимый объем выборки, который обеспечит требуемую точность полученных статистических характеристик при заданном уровне вероятности.
Предельную ошибку повторной собственно случайной выборки можно записать через среднюю ошибку:
![]() (63)
(63)
Отсюда можно вывести формулу для определения необходимого объема собственно случайной повторной выборки:
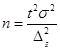 (64)
(64)
Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если мы получили, что необходимый объем выборки составляет 598,1 единицы, то для достижения желаемого результата обследованием должны быть охвачены 599 единиц.
Пример 3. Вам необходимо провести исследование с вероятностью 95,4 %, посвященное оценке удовлетворенности качеством работы менеджеров, отвечающих за поддержку клиентов по телефону. Качество обслуживания оценивается клиентами в баллах по пятибалльной шкале. Из прошлых исследований известно, что среднее квадратическое отклонение в оценках качества составляет 0,5 балла. Предельно допустимая ошибка данного исследования не должна превышать 5 %. Какое минимальное количество респондентов вам необходимо опросить в порядке собственно случайной повторной выборки для решения данной проблемы?
Решение:
Поскольку при вероятности 0,954 значение t = 2, находим необходимый объем выборки:
![]()
Следовательно, обследованию необходимо подвергнуть не менее 400 респондентов на предмет оценки удовлетворенности качеством работы менеджеров из службы поддержки.
В соответствии с формулой 16 необходимый объем выборки будет тем больше, чем выше заданный уровень вероятности и чем сильнее варьирует наблюдаемый признак. В то же время повышение допустимой предельной ошибки выборки приводит к снижению необходимого ее объема.
При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение:
![]() (65)
(65)
Это значение подставляется в формулу 64 в качестве значения дисперсии.
Необходимый объем собственно случайной бесповторной выборки определяется по следующей формуле:
![]() (66)
(66)
При этом важно помнить, что в процессе проведения вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц. Например, подставив в данную формулу общее количество заказов, выраженное в тысячах единиц, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах единиц, как это иногда бывает в других расчетах. Результат вычислений будет неверен.
Пример 4. Требуется определить объем выборки для исследования удовлетворенности постоянных клиентов качеством работы персональных менеджеров с вероятностью 95,4 %. Качество работы оценивается клиентами в баллах по пятибалльной шкале. Из прошлых исследований известно, что среднее квадратическое отклонение в оценках качества составляет 0,5 балла. Предельно допустимая ошибка данного исследования не должна превышать 0,05. Какое минимальное количество постоянных клиентов вам необходимо опросить в порядке собственно случайной бесповторной выборки, если общий список постоянных клиентов компании составляет 1000 человек?
Решение:
![]()
Следовательно, для обеспечения репрезентативности данных исследования выборочному обследованию методом бесповторного отбора необходимо подвергнуть не менее 286 постоянных клиентов компании.
Для определения численности механической выборки используют формулы, применяемые при собственно случайном бесповторном отборе. При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление в меньшую сторону для получения целочисленного интервала отбора.
Пример 5. Вы контролируете работу 284 супермаркетов вашего района. Определим, сколько из них необходимо отобрать в порядке механического отбора для выявления нарушений политики вашей компании с ошибкой +/-2 нарушения и с вероятностью 0,95. По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение численности нарушений составляет 3 единицы.
Решение:
Расчет проведем, используя формулу 66:
![]()
С учетом полученного необходимого объема выборки (9 супермаркетов) определим интервал отбора: 284 / 9 = 31,56. Определенный таким способом интервал всегда округляется в меньшую сторону, так как при округлении в большую сторону произведенная выборка не достигнет рассчитанного по формуле необходимого объема. Следовательно, в нашем примере, из общего списка супермаркетов необходимо отобрать для обследования каждый 31-й магазин. При этом процент отбора составит 3,2 % (100 % / 31, или 9 / 284).
1. Какие преимущества и недостатки по сравнению со сплошным наблюдением имеет выборочное наблюдение?
2. В чем отличие бесповторного от повторного отбора?
3. Что показывает предельная ошибка выборки? От каких основных факторов зависит ее уровень?
4. Что показывает средняя ошибка выборки?
5. Что понимается под доверительной вероятностью и коэффициентом доверия? Какая существует между ними зависимость?
6. В чем отличие механического отбора от случайного?
7. Какие проблемы возникают при использовании систематической выборки?
8. Что представляет собой стратифицированная выборка?
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Салин В.Н., Чурилова Э.Ю. Практикум по курсу «Статистика» (в системе STATISTICA). – М.: Социальные отношения, 2006.
3. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
5. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Задание 1.
Определите вид выборки – собственно случайная, механическая, стратифицированная – использованный при проведении исследования, указанного в таблице.
|
Содержание исследования |
Вид выборки |
|
А) Выборочное обследование бюджетов домашних хозяйств Центрального федерального округа, реализованное по областям ЦФО (внутри областей домашние хозяйства отбирались случайным образом пропорционально общему количеству домохозяйств). |
|
|
Б) Опрос покупателей телевизоров по анкетам, вложенным в упаковку продукта. |
|
|
В) Выборочное обследование размера расходов посетителей ресторана за неделю, проведенное путем анализа каждого 10-го чека из общего списка чеков за выбранную неделю. |
|
|
Г) Обследование прохожих города на предмет выяснения степени владения каким-либо иностранным языком. |
|
|
Д) Обследование 25 % студентов вуза на предмет их карьерных планов, проведенное по каждому факультету отдельно. |
|
Задание 2.
Определите необходимый объем выборки для обследования среднедушевых денежных доходов населения области методом собственно случайного повторного отбора, чтобы с вероятностью 0,997 предельная ошибка выборки не превышала 300 руб, если известно, что среднее квадратическое отклонение величины среднедушевого денежного дохода составляет 2783 руб.
Задание 3.
Количество корпоративных клиентов-юридических лиц банка составляет 750. Планируется проведение механического выборочного обследования с целью определения уровня удовлетворенности работой новой системы интернет-банкинга (в баллах по пятибалльной системе). Определите сколько и каких клиентов из общего списка необходимо опросить, чтобы с вероятностью 0,9545 предельная ошибка не превысила 0,3 балла, если известно, что дисперсия оценок системы интернет-банкинга клиентами составляет 3,85.
Цель изучения темы состоит в формировании системы знаний и компетенций об основных статистических категориях выявления и оценки силы взаимосвязи между социально-экономическими явлениями, способах расчета, оценки и интерпретации показателей взаимосвязи между социально-экономическими явлениями, выраженными неколичественными признаками.
В результате успешного освоения темы Вы:
Узнаете:
· какие виды взаимосвязи существуют в экономическом анализе;
· какие методы используются при изучении связей между социально-экономическими явлениями;
· что представляют собой линейная и нелинейная связи;
· что означает взаимная сопряженность признаков и каким образом подготовить исходные данные для ее оценки;
· с помощью каких коэффициентов измеряется взаимосвязь между качественными признаками.
Приобретете компетенции:
· владение методами количественного анализа, теоретического и экспериментального исследования;
· владение основными методами, способами и средствами получения, хранения, переработки информации, навыками работы с компьютером как средством управления информацией;
· понимание роли и значения информации в развитии современного общества и экономических знаний;
· способность оценивать воздействие макроэкономической среды на функционирование организаций и органов государственного и муниципального управления;
· умение применять количественные и качественные методы анализа при принятии управленческих решений;
· умение различать виды взаимосвязи;
· умение строить и анализировать диаграмму рассеяния;
· умение составлять таблицы взаимной сопряженности качественных признаков размерностью 2х2 и большей;
· умение выбирать вид и рассчитывать значения коэффициентов взаимосвязи между качественными признаками.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· факторные и результативные признаки;
· функциональная связь;
· корреляционная связь;
· прямая и обратная связь;
· линейная и нелинейная связь;
· ложная корреляция;
· диаграмма рассеяния;
· таблица сопряженности;
· коэффициент ассоциации;
· коэффициент контингенции;
· коэффициент взаимной сопряженности Пирсона;
· коэффициент взаимной сопряженности Чупрова;
· показатель взаимной сопряженности.
Вопросы темы:
1. Классификация видов и методов изучения взаимосвязи.
2. Графический метод выявления взаимосвязи.
3. Изучение взаимосвязи между качественными признаками.
Теоретический материал по теме
Исследование объективно существующих связей между социально-экономическими явлениями и процессами является важнейшей задачей статистики. Понимание, как изменение одного из исследуемых показателей отразится на изменении другого, необходимо при регулировании и управлении любыми системами и процессами, чтобы правильно оценивать последствия принимаемых управленческих решений.
Большинство финансово-экономических процессов – это результат одновременного взаимодействия большого числа составляющих их элементов, представляющих собой выраженные в форме показателей различные количественные и качественные признаки.
Признаки по их сущности и значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменения других связанных с ними признаков, называются факторными, или просто факторами и обозначаются Х. Признаки, изменяющиеся под действием факторов, называются результативными и обозначаются Y.
При исследовании взаимосвязи между одним факторным и одним результативным признаками или между двумя факторными признаками говорят о двумерных данных, а при изучении влияния нескольких факторных признаков на один результативный – о многомерных данных.
В статистике различают функциональную и корреляционную связи. Функциональной называют связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
Если зависимость проявляется не в каждом отдельном случае, а в общем, среднем, при большом числе наблюдений, то такая зависимость называется корреляционной. При корреляционной связи изменение среднего значения результативного признака обусловлено изменением признака-фактора и при одинаковом значении факторного признака величина признака-результата у разных единиц совокупности может в силу индивидуальных особенностей различаться.
Связи между явлениями и их признаками классифицируются по направлению, тесноте (силе связи) и аналитическому выражению (рис. 20)
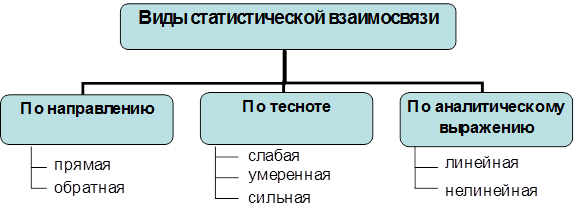
Рис. 20. Классификация видов взаимосвязи
По направлению выделяют связь прямую и обратную. Прямая – это связь, при которой с увеличением или с уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного признака. Так, рост объемов производства способствует увеличению прибыли предприятия. В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении – с увеличением или с уменьшением значений факторного признака происходит уменьшение или увеличение значений признака-результата. Так, снижение себестоимости единицы производимой продукции вызывает рост прибыли.
Для измерения тесноты связи используют значение коэффициента корреляции. Он изменяется в пределах от -1 до +1. Знак (+) говорит о прямой связи, а (-) об обратной (табл. 41):
Таблица 41.
Количественные критерии оценки тесноты связи
|
Значение коэффициента корреляции |
Теснота связи |
|
до ±0,3 |
практически отсутствует |
|
±0,3 – ±0,5 |
слабая |
|
±0,5 – ±0,7 |
умеренная |
|
±0,7 – ±1,0 |
сильная |
По аналитическому выражению выделяют связи линейные и нелинейные. Если
статистическая связь между явлениями X и Y может быть
приблизительно выражена уравнением прямой линии (![]() ),
то ее называют линейной. Если же связь может быть выражена уравнением
какой-либо кривой линии, например параболы (
),
то ее называют линейной. Если же связь может быть выражена уравнением
какой-либо кривой линии, например параболы (![]() ),
то такую связь называют нелинейной, или криволинейной.
),
то такую связь называют нелинейной, или криволинейной.
Для выявления и анализа связи статистика использует следующие основные методы:
· графический метод – построение диаграммы рассеяния;
· метод корреляционного анализа – выявление наличия, силы и направления взаимосвязи между признаками;
· метод регрессионного анализа – построение модели взаимосвязи, позволяющей получать расчетные значения результативного показателя на основе значений факторного признака.
Причинную обусловленность и корреляцию нельзя считать синонимами. Корреляция не всегда дает объяснение, почему исследуемые переменные в двумерной совокупности связаны между собой. Следует иметь в виду, что корреляция бывает и без причинной обусловленности: она представляет собой число, которое говорит, что большим значениям одного фактора соответствуют большие значения другого (или наоборот). Корреляция всего лишь указывает, что между этими величинами наблюдается определенное соответствие.
Наиболее распространенной причиной существования корреляции без причинной обусловленности является наличие некоторого скрытого третьего фактора, создающего впечатление, будто одна переменная выступает причиной другой. Однако реальной причиной для каждой из этих двух переменных является неизвестная третья.
Под термином ложная корреляция понимают высокую корреляцию, которая обеспечивается действием третьего фактора. Например, если рассчитать значение коэффициента корреляции между такими показателями, как «размер ущерба имуществу от пожара» и «количество пожарных, участвовавших в тушении пожара», то это будет величина, близкая к 1. Однако, конечно же, нельзя утверждать, что причиной высокого размера ущерба является большое количество пожарных, действиями которых и нанесен ущерб имуществу. Безусловно, пожарные, заливая огонь пеной или водой, могут нечаянно повредить электрокабели или офисную технику, но в любом случае причиной высокой корреляции между ущербом имуществу и количеством пожарных является третий фактор – масштаб самого пожара. Чем более сложный и масштабный пожар, тем больший урон имуществу он наносит и тем большее число пожарных требуется для его тушения.
Графический метод предполагает изображение взаимосвязи двух признаков с помощью диаграммы рассеяния (поля корреляции). Диаграмма рассеяния представляет каждую единицу совокупности в виде точки в пространстве двух измерений, соответствующих двум факторам. Переменная, которая рассматривается как «причина», обозначается х и указывается на оси абсцисс. Переменная, изменяющаяся под влиянием этой причины, обозначается y и указывается по оси ординат.
Для построения диаграммы рассеяния необходимо в
системе координат на оси Х отложить значения факторного признака, а на
оси Y – результативного и каждое пересечение линий,
проводимых через эти оси, обозначить соответствующими точками. Чем сильнее
связь между признаками, тем теснее будут группи
роваться точки вокруг определенной линии,
выражающей форму связи (рис. 21).
![]()

Рис. 21. Диаграмма рассеяния (поле корреляции)
При отсутствии связи диаграмма рассеяния точек имеет вид либо круглого, либо овального облака (причем овал может быть направлен как горизонтально, так и вертикально, но не иметь наклона) (рис. 22).
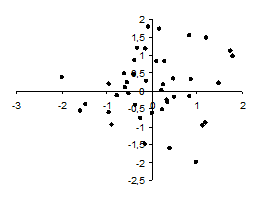
Рис. 22. Диаграмма рассеяния, свидетельствующая об отсутствии взаимосвязи между двумя признаками
Легче всего поддается анализу и интерпретации двумерная совокупность данных, выраженная в форме линейной взаимосвязи. Визуально взаимосвязь проявляется в том, что точки на диаграмме рассеяния концентрируются вокруг условной прямой линии. Они могут как довольно тесно концентрироваться, почти точно попадая на прямую линию (рис. 23), так и быть разбросаны достаточно широко, образуя некоторое облако (рис. 24).
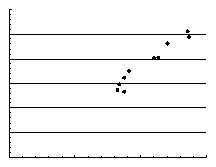
Рис. 23. Диаграмма рассеяния, выражающая линейную положительную взаимосвязь
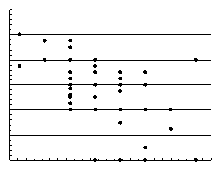
Рис. 24. Диаграмма рассеяния, выражающая линейную отрицательную взаимосвязь
При нелинейной взаимосвязи точки на диаграмме рассеяния группируются вокруг некоторой кривой линии. Поскольку разновидностей кривых линий существует множество, анализ такой взаимосвязи существенно осложнен. Приведем пример двух наиболее распространенных видов нелинейной связи (рис. 25 и 26):
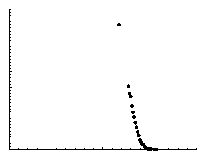
Рис. 25. Диаграмма рассеяния, характеризующая взаимосвязь, выраженную уравнением гиперболы
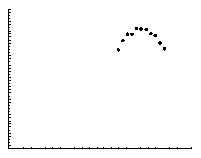
Рис. 26. Диаграмма рассеяния, характеризующая взаимосвязь, выраженную уравнением параболы
Пример 1. Построим диаграмму рассеяния по данным таблицы 42 и охарактеризуем тип взаимосвязи, которую иллюстрирует диаграмма рассеяния.
Таблица 42.
Итоги работы менеджеров по продаже полиграфической продукции
|
Менеджер проекта |
Величина списка контактов, тыс. чел. |
Объем продаж, тыс. руб. |
|
1 |
168 |
5178 |
|
2 |
21 |
2370 |
|
3 |
94 |
3591 |
|
4 |
39 |
2056 |
|
5 |
249 |
7325 |
|
6 |
43 |
2449 |
|
7 |
589 |
15708 |
|
8 |
41 |
2469 |
При построении диаграммы рассеяния для данной двумерной совокупности данных необходимо, во-первых, определить факторный и результативный признаки. Так как затраченные усилия влияют на результат, следовательно, число контактов с клиентами признаем факторным признаком и изображаем его на горизонтальной оси, а объем продаж – результативным признаком и располагаем его по вертикальной оси. Далее изображаем точки, иллюстрирующие, как величина объема продаж изменяется от количества контактов. Нанеся все точки на график, получим диаграмму рассеяния, которая представлена на рис. 27.
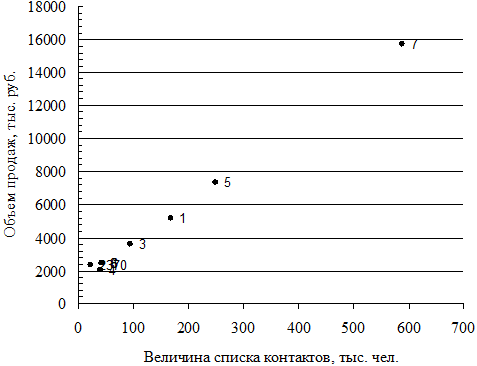
Рис. 27. Взаимосвязь между количеством контактов и объемом продаж полиграфической продукции
На диаграмме рассеяния представлена информация как о каждой отдельной единице совокупности, так и о взаимосвязи между ними. Взаимосвязь между количеством контактов и объемом продаж можно признать положительной: точки на диаграмме выстраиваются снизу вверх при движении слева направо. Это свидетельствует о том, что менеджеры, имеющие больше количество контактов с клиентами, обеспечили компании и большие объемы сбыта (чем больше значения х, тем выше расположены точки на диаграмме). Полученную взаимосвязь можно признать линейной, что видно и по форме области концентрации точек на диаграмме рассеяния, которые практически выстраиваются в прямую линию.
Значения бизнес-показателей, анализируемых в ходе исследования, не всегда имеют количественное выражение. При обработке информации менеджер-аналитик часто сталкивается с показателями, выраженными в номинальной шкале, например: пол, должность сотрудника, уровень профессионального образования и т.п. Также информация может быть представлена по альтернативным признакам, принимающим только два варианта «да» (1) и «нет» (0) (например: курение сотрудника, наличие или отсутствие у него детей, наличие/отсутствие замечаний за нарушение производственной дисциплины и т.п.). При экспресс-опросах, например, по результатам обучающих мероприятий, используются вопросы, призванные выявить степень удовлетворенности участников обучения его результатами (удовлетворен / не удовлетворен), изменение отношения к предмету обучения (изменилось / не изменилось, ниже среднего / среднее / выше среднего, улучшилось / не изменилось / ухудшилось). Такие показатели являются качественными, и известные методы количественного анализа для их анализа и исследования неприменимы.
Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух вариантов, применяются коэффициенты ассоциации и контингенции.
Для их вычисления строится таблица сопряженности [2 х 2], которая показывает связь между двумя явлениями, каждое из которых состоит из двух качественно отличных друг от друга значений признака (например, изделие годное или бракованное). Как правило, в строках располагают варианты факторного признака, а в столбцах – результативного. Если признак один и тот же, а различие состоит в объектах, то в строках и столбцах используют одинаковый порядок расположения вариантов. Например, исследуя взаимосвязь между факторным признаком «наличие высшего образования у родителей (имеют / не имеют)» и «наличие высшего образования у детей (имеют / не имеют)», вариант «имеет высшее образование» следует расположить в первой строке и в первом столбце таблицы сопряженности этих признаков.
Таблица 43.
Таблица взаимной сопряженности для вычисления коэффициентов ассоциации и контингенции
|
y x |
I |
II |
Всего: |
|
I |
n11 |
n12 |
n11+n12 |
|
II |
n21 |
n22 |
n21+n22 |
|
Всего: |
n11+n21 |
n12+n22 |
n11+n12+n21+n22 |
Коэффициент ассоциации Ка вычисляют по формуле:
![]() , (67)
, (67)
где
n11 – число единиц, имеющих значения x1 и y1;
n12 – число единиц, имеющих значения x1 и y2;
n21 – число единиц, имеющих значения x2 и y1;
n22 – число единиц, имеющих значения x2 и y2.
Коэффициент ассоциации принимает значения в интервале [-1; 1]. При равенстве коэффициента ассоциации нулю говорят об отсутствии связи между изучаемыми признаками.
Коэффициент контингенции Кк считается более надежной мерой связи и определяется по формуле:
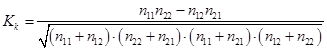 (68)
(68)
Коэффициент контингенции принимает значения в интервале [0; 1]. Коэффициент контингенции принимает нулевое значение при отсутствии связи между изучаемыми показателями и равен единице – при функциональной зависимости между ними.
Коэффициент контингенции всегда
меньше коэффициента ассоциации. Связь считается подтвержденной, если ![]() или
или![]() .
.
Пример 2. Исследуем связь между активностью участия студентов в практических занятиях и результатом тестирования по теме курса. Результаты обследования характеризуются следующими данными (таблица 44).
Таблица 44.
Зависимость результата тестирования по теме от активности участия студентов в практических занятиях
|
Участие в практическом занятии |
Количество студентов |
Из них |
|
|
успешно сдали тест по теме |
не сдали тест по теме |
||
|
Активное Пассивное |
100 100 |
78 32 |
22 68 |
|
Итого |
200 |
110 |
90 |
![]()
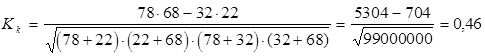
Таким образом, связь между результатом прохождения итогового тестирования по теме и активностью участия студента в практическом занятии сильная и прямая.
Когда хотя бы один из качественных признаков принимает более двух вариантов значений, то для определения тесноты связи применяются коэффициенты взаимной сопряженности Пирсона и Чупрова. Вспомогательная таблица, используемая для расчета коэффициентов, имеет следующий вид:
Таблица 45.
Вспомогательная таблица для расчета коэффициентов взаимной сопряженности Пирсона и Чупрова
|
Y Х |
I |
II |
III |
… |
Всего |
|
I |
nx1y1 |
nx1y2 |
nx1y3 |
… |
nx1 |
|
II |
nx2y1 |
nx2y2 |
nx2y3 |
… |
nx2 |
|
III |
nx3y1 |
nx3y2 |
nx3y3 |
… |
nx3 |
|
… |
… |
… |
… |
… |
… |
|
Итого |
ny1 |
ny2 |
ny3 |
… |
n |
Коэффициент Пирсона КП и коэффициент Чупрова КЧ вычисляются по следующим формулам:
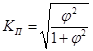 (69)
(69)
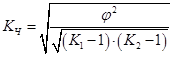 (70)
(70)
где
K1 – число значений (групп) первого признака;
K2 – число значений (групп) второго признака;
![]() – показатель взаимной
сопряженности.
– показатель взаимной
сопряженности.
Показатель взаимной сопряженности ![]() определяется
как сумма отношений квадратов частот каждой клетки таблицы к произведению
итоговых частот соответствующего столбца и строки.
определяется
как сумма отношений квадратов частот каждой клетки таблицы к произведению
итоговых частот соответствующего столбца и строки.
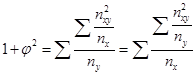 (71)
(71)
Вычитая из этой суммы «1»,
получим величину![]() :
:
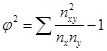 (72)
(72)
Коэффициенты взаимной сопряженности принимают значения в интервале [0; 1]. Равенство коэффициентов нулю означает отсутствие связи, равенство единице – полную взаимосвязь.
Пример 3. С помощью коэффициентов взаимной сопряженности Пирсона и Чупрова исследуем взаимосвязь показателей «частота опозданий сотрудника» и «оценка качества работы сотрудника его руководителем».
Таблица 46.
Зависимость оценки качества работы сотрудника его руководителем от частоты опозданий сотрудника
Решение:
1. Рассчитаем показатель взаимной
сопряженности ![]() :
:
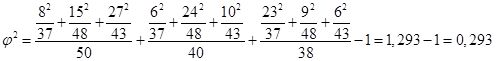
2. Найдем значения коэффициентов взаимной сопряженности согласно формулам:
![]()
![]()
Таким образом, связь между частотой опозданий сотрудников и оценкой качества их работы руководителем можно признать статистически значимой и средней по силе влияния.
1. В чем различия между функциональной и корреляционной связью?
2. В каких случаях можно говорить о прямой, а в каких – об обратной зависимости между изучаемыми признаками?
3. Что такое диаграмма рассеяния и как она строится?
4. Как выглядит расположение точек на диаграмме рассеяния:
а) при нелинейной связи между x и y;
б) при отсутствии взаимосвязи между x и y?
5. Что такое ложная корреляция?
6. Что представляет собой таблица сопряженности? Какие размерности таблиц сопряженности вы знаете?
7. Для каких качественных данных используется расчет коэффициента ассоциации и контингенции?
8. Когда для оценки взаимосвязи используются коэффициенты взаимной сопряженности Пирсона и Чупрова?
9. Как интерпретируются количественные значения коэффициентов взаимной сопряженности? Какие критические значения для них существуют?
10. Какие коэффициенты следует применить для оценки взаимосвязи между показателями:
а) «пол сотрудника» и «наличие ученой степени»?
б) «уровень образования сотрудника (полное среднее, среднее профессиональное, высшее)» и «оценка степени корпоративной лояльности» (высокая, средняя, низкая)»?
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Задание 1.
При помощи диаграммы рассеяния оцените направление взаимосвязи между показателями, указанными в таблице.
|
Номер п.п. |
Данные для анализа взаимосвязи |
Направление взаимосвязи |
|||||||||||||||||||||||||||
|
1. |
|
|
|||||||||||||||||||||||||||
|
2. |
|
|
Задание 2.
По итогам проведения тренинга были получены следующие результаты анкетирования его участников (таблицы ниже).
Посещаемость занятий сотрудниками
|
Пол |
иногда пропускал |
посещал всегда |
Итого: |
|
мужской |
7 |
5 |
12 |
|
Женский |
2 |
6 |
8 |
|
Итого |
9 |
11 |
20 |
Таблица сопряженности оценки сотрудниками качества работы тренера и общей удовлетворенности посещением тренинга
|
оценка тренера |
оценка тренинга |
Итого: |
||
|
удовлетворительно |
хорошо |
отлично |
||
|
удовлетворительно |
4 |
1 |
0 |
5 |
|
хорошо |
1 |
6 |
1 |
8 |
|
отлично |
0 |
2 |
5 |
7 |
|
Итого: |
5 |
9 |
6 |
20 |
При помощи известных вам методов определите:
а) повлиял ли пол сотрудника на посещение занятий тренинга?
б) есть ли взаимосвязь (и если есть, то какая) между оценкой участником тренинга работы тренера и общей оценкой его удовлетворенностью посещением тренинга?
Цель изучения темы состоит в формировании системы знаний и компетенций о статистических методах, применяемых для анализа взаимосвязи между социально-экономическими явлениями, построения ее моделей, оценке и интерпретации параметров этих моделей.
В результате успешного освоения темы Вы:
Узнаете:
· в чем разница между корреляционным и регрессионным анализом;
· основные условия применения корреляционного анализа;
· для чего используется линейный коэффициент корреляции и как интерпретируется его значение;
· основные условия применения регрессионного анализа;
· для чего используется парная линейная регрессия;
· основные правила интерпретации показателей связи.
Приобретете компетенции:
· владение методами количественного анализа и моделирования, теоретического и экспериментального исследования;
· владение основными методами, способами и средствами получения, хранения, переработки информации, навыками работы с компьютером как средством управления информацией;
· понимание роли и значения информации в развитии современного общества и экономических знаний;
· способность оценивать воздействие макроэкономической среды на функционирование организаций и органов государственного и муниципального управления;
· умение применять количественные и качественные методы анализа при принятии управленческих решений и строить экономические, финансовые и организационно-управленческие модели;
· способность оценивать эффективность использования различных систем учета и распределения затрат, иметь навыки калькулирования и анализа себестоимости продукции и способностью принимать обоснованные управленческие решения на основе данных управленческого учета;
· способность обосновывать решения в сфере управления оборотным капиталом и выбора источника финансирования;
· способность рассчитывать парный линейный коэффициент корреляции и делать по нему выводы;
· способность рассчитывать параметры линейного и нелинейного уравнения регрессии;
· способность интерпретировать коэффициенты регрессии и эластичности.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· корреляционный анализ;
· регрессионный анализ;
· линейный коэффициент корреляции Пирсона;
· уравнение регрессии;
· коэффициент регрессии;
· парная линейная регрессия;
· теоретическое корреляционное отношение;
· коэффициент эластичности.
Вопросы темы:
1. Корреляционный анализ.
2. Регрессионный анализ.
Теоретический материал по теме
Корреляционный анализ используется для количественного определения тесноты и направления связи между признаками при помощи коэффициента корреляции. Знаки при коэффициенте корреляции характеризуют направление связи между изучаемыми признаками, а по его значению характеризуют силу или тесноту связи между признаками. Корреляционный анализ дает ответы на следующие вопросы:
· существует ли между рассматриваемыми признаками взаимосвязь вообще?
· если связь существует, то каково ее направление: значения результативного признака растут или уменьшаются под влиянием факторного?
· насколько тесной является эта взаимосвязь?
Для проведения корреляционного анализа необходимо выполнение следующих условий:
1. Признаки, между которыми исследуется взаимосвязь, должны иметь количественное выражение, т.е. каждая единица совокупности должна характеризоваться двумя числами – значением факторного и значением результативного признаков.
2. Данные по каждому признаку должны иметь одинаковую размерность и методологию расчета. Например, изучая зависимость заработной платы сотрудника от стажа его работы, нельзя, чтобы у части сотрудников стаж был указан в месяцах, а у части – в годах, или у одних брался номинальный (до вычета налогов), а у других – реальный размер заработной платы. В данных не должно быть пропусков (например, неизвестен стаж хотя бы у одного сотрудника). Единицы, имеющие пропуски в значениях факторного или результативного признаков, исключаются из исходных данных.
3. Рассматриваемая совокупность должна быть однородна по составу единиц и существенна по их количеству. Например, качество анализа будет выше, если рассматривать взаимосвязь зарплаты и стажа по категориям сотрудников (вспомогательные работники, рабочие, административный персонал, менеджеры и т.п.), используя данные как можно большего числа сотрудников каждой категории.
Если по аналитическому выражению связь между признаками можно описать уравнением прямой, для выявления наличия, направленности и тесноты связи рассчитывают линейный коэффициент корреляции.
Линейный коэффициент корреляции Пирсона, обозначаемый r, характеризует тесноту и направление связи между двумя признаками в случае наличия между ними линейной зависимости.
Линейный коэффициент корреляции изменяется в пределах
от -1 до +1: ![]() . Корреляция, равная 1, указывает
на идеальную взаимосвязь в виде прямой линии, причем более высокие значения
одной переменной соответствуют предсказуемым более высоким значениям другой
переменной. Корреляция, равная -1, указывает на отрицательную идеальную
взаимосвязь в виде прямой линии, причем одна переменная уменьшается с ростом
другой.
. Корреляция, равная 1, указывает
на идеальную взаимосвязь в виде прямой линии, причем более высокие значения
одной переменной соответствуют предсказуемым более высоким значениям другой
переменной. Корреляция, равная -1, указывает на отрицательную идеальную
взаимосвязь в виде прямой линии, причем одна переменная уменьшается с ростом
другой.
Абсолютное значение коэффициента корреляции указывает на силу взаимосвязи, а знак (+ или -) указывает направление (увеличение или уменьшение) связи. В таблице 47 показано, как следует интерпретировать связь в каждом конкретном случае.
Таблица 47.
Интерпретация значения линейного коэффициента корреляции
|
Значение r |
Характеристика связи |
Интерпретация связи |
Наглядное представление связи |
|
r = 0 |
Взаимосвязь отсутствует |
- |
Совершенно случайное облако, не имеющее ориентации ни вверх, ни вниз при движении вправо |
|
Близко к 0, но > 0 |
незначительная положительная взаимосвязь |
С увеличением факторного признака слабо возрастает результативный признак |
Точки данных образуют случайное облако с незначительной ориентацией вверх и вправо |
|
Близко к 1 |
сильная положительная взаимосвязь |
С увеличением факторного признака увеличивается результативный признак |
Точки данных довольно плотно сгруппированы (с небольшим разбросом) вокруг прямой линии, направленной вверх и вправо |
|
Близко к 0, но < 0 |
незначительная отрицательная взаимосвязь |
С увеличением факторного признака незначительно уменьшается результативный – и наоборот |
Точки данных образуют случайное облако с незначительной ориентацией вниз и вправо |
|
Близко к -1 |
сильная отрицательная взаимосвязь |
С увеличением факторного признака уменьшается результативный, и наоборот |
Точки данных довольно плотно сгруппированы (с небольшим разбросом) вокруг прямой линии, направленной вниз и вправо |
|
r = 1 |
функциональная |
Определенному значению факторного признака соответствует строго одно значение результативного |
Идеальная положительная взаимосвязь: все точки данных располагаются строго на прямой линии, направленной вверх и вправо |
|
r = -1 |
Идеальная отрицательная взаимосвязь: все точки данных располагаются строго на прямой линии, направленной вниз и вправо |
Расчет линейного коэффициента корреляции осуществляется по формуле:
![]() , (73)
, (73)
где
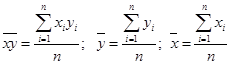 ;
;
![]() ;
;
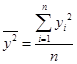 ;
;
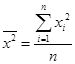 ;
;
n – число наблюдений.
Вычисление линейного коэффициента корреляции удобно проводить при помощи вспомогательной таблицы (табл. 48):
Таблица 48.
Вспомогательная таблица для расчета линейного коэффициента корреляции
|
№ объекта, n |
Факторный признак, хi |
Результативный признак, yi |
yi2 (гр. 3 * гр. 3) |
xi2 (гр. 2 *гр. 2) |
xiyi (гр. 2 *гр. 3) |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
x1 |
y1 |
y12 |
x12 |
x1∙y1 |
|
2 |
x2 |
y2 |
y22 |
x22 |
x2∙y2 |
|
… |
… |
… |
… |
… |
… |
|
n |
Xn |
Yn |
Yn2 |
Xn2 |
Xn∙Yn |
|
Итого |
|
|
|
|
|
|
Среднее значение |
|
|
|
|
|
Если преобразовать формулу 73, то линейный коэффициент корреляции можно вычислить, используя итоговые суммы из таблицы 48:
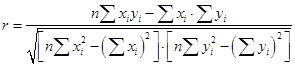 (74)
(74)
Числитель выражает взаимодействие двух переменных и определяет знак корреляции. Если между переменными существует сильная положительная взаимосвязь, числитель примет положительное значение, если сильная обратная – числитель примет отрицательное значение. Знаменатель формул 73 и 74 всегда положителен, т.к. он является произведением средних квадратических отклонений по X и Y, которые всегда больше нуля, т.к. рассчитываются как квадратный корень из дисперсии.
Пример 1. Определим тесноту взаимосвязи между величиной товарооборота и количеством обслуженных клиентов десяти крупнейших туристических компаний/групп по итогам 2011 г. (по данным kommersant.ru, табл. 49).
Таблица 49.
Показатели деятельности крупнейших туристических компаний/групп по итогам 2011 г.
(по данным kommersant.ru)
|
№ п.п. |
Компания/группа (бренды) |
Товарооборот (млрд руб.) y |
Количество клиентов (млн. чел.), x |
Расчетные графы |
||
|
у2 |
х2 |
ху |
||||
|
1. |
OTI Россия (Coral Travel; Sunmar Tour, A-Class Travel, Blue Sky) |
29,5 |
1,05 |
870,25 |
1,1025 |
30,98 |
|
2. |
«Библио-Глобус» |
15,8 |
0,52 |
249,64 |
0,2704 |
8,22 |
|
3. |
TUI Russia & CIS |
15,4 |
0,51 |
237,16 |
0,2601 |
7,85 |
|
4. |
Приморское агентство авиационных компаний (Всероссийская сеть «БИЛЕТУР») |
11,8 |
0,63 |
139,24 |
0,3969 |
7,43 |
|
5. |
Трансаэро Тур |
6,3 |
0,36 |
39,69 |
0,1296 |
2,27 |
|
6. |
«Южный крест» |
5,6 |
0,17 |
31,36 |
0,0289 |
0,95 |
|
7. |
Клуб путешествий «Крылья» |
5,6 |
0,47 |
31,36 |
0,2209 |
2,63 |
|
8. |
Академсервис |
5,5 |
0,57 |
30,25 |
0,3249 |
3,14 |
|
9. |
PAC Group |
5,3 |
0,16 |
28,09 |
0,0256 |
0,85 |
|
10. |
«КМП групп» |
4,0 |
0,20 |
16,00 |
0,0400 |
0,80 |
|
Итого |
104,8 |
4,64 |
1 673,04 |
2,7998 |
65,11 |
|
|
Среднее значение |
10,48 |
0,464 |
167,304 |
0,27998 |
6,511 |
|
Диаграмма рассеяния, представленная на рис. 28, отображает положительную по направлению и близкую к линейной взаимосвязь между товарооборотом компаний (результативный признак y) и количеством обслуженных клиентов (факторный признак x) – точки на графике поднимаются вверх при движении по оси x, ось области концентрации облака точек имеет вид, наиболее близкий по форме к прямой линии.
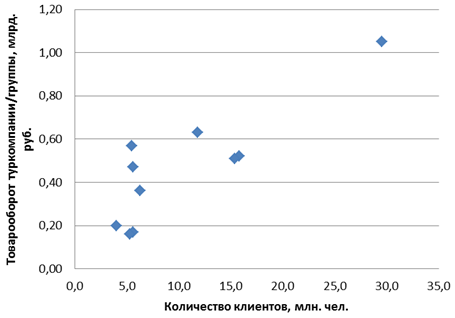
Рис. 28. Диаграмма рассеяния, характеризующая взаимосвязь между величиной товарооборота и количеством обслуженных клиентов наиболее крупных по итогам 2011 г. туристических компаний/групп
Подтвердим предположение о наличии положительной связи на основании расчета линейного коэффициента корреляции.
1. Используя формулу (73), получаем:
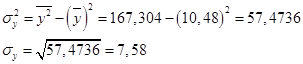
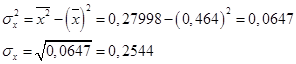
![]()
2. По формуле (74) значение коэффициента корреляции составило:
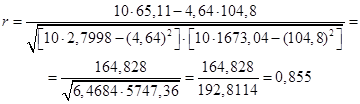
Таким образом, можно сделать вывод, что между величиной товарооборота туристической компании и количеством обслуженных ею клиентов существует сильная по тесноте и прямая по направлению взаимосвязь.
Существенно облегчить и ускорить расчет показателей взаимосвязи позволяет широко распространенный стандартный табличный редактор MS Excel. Для расчета величины парного линейного коэффициента корреляции Пирсона необходимо в редакторе данных построить таблицу с исходными значениями анализируемых показателей и ввести вручную или вызвать с помощью меню специальную команду-функцию PEARSON.
Синтаксис этой команды имеет следующий вид:
=PEARSON(массив 1; массив 2) (75)
Параметры команды, указанные в скобочках, задаются пользователем и имеют следующее значение:
Массив 1 – диапазон данных в исходной таблице, как правило, в столбце, в котором указаны значения факторного показателя x;
Массив 2 – диапазон данных в исходной таблице, как правило, в столбце, в котором указаны значения результативного показателя y.
Вводить команду PEARSON можно в командной строке редактора или непосредственно в ячейке, в которой мы хотим получить значение коэффициента взаимосвязи.
Проиллюстрируем использование MS Excel для расчета взаимосвязи показателей примера 1 (таблица 49).
Исходные данные о товарообороте и количестве клиентов крупнейших туристических компаний РФ в 2011 г. оформлены в MS Excel в виде таблицы, представленной на рис. 29.
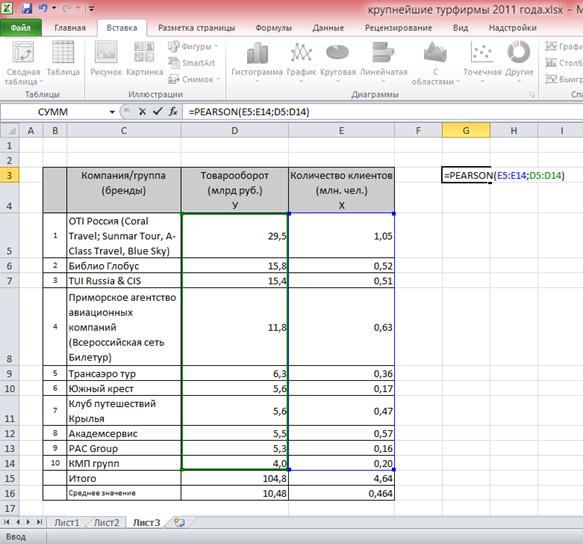
Рис. 29. Иллюстрация применения команды PEARSON в MS Excel
В этой таблице в столбце Е, а именно в ячейках с Е5 по Е14, указаны данные о количестве клиентов компаний – показатель x, а в столбце D ячейки D5:D14 содержат данные о товарообороте туркомпаний – показатель y. Очень важно проверить, чтобы формат ячеек, содержащих данные, был именно числовым, а не текстовым, поскольку текстовые и пустые ячейки при расчете коэффициента корреляции Пирсона в MS Excel не учитываются, что искажает результат вычислений и не позволяет правильно оценить взаимосвязь между показателями!
Установим курсор в ячейку G3 и воспользуемся командой PEARSON. Для этого в ячейку мы введем следующие символы: «=PEARSON(» (кавычки не вводятся!) (рис. 29). После ввода начальных символов команды MS Excel выведет на экран для подсказки внизу ячейки синтаксис формулы и будет ждать действий пользователя по заданию ее параметров. Далее произведем следующие действия:
· для задания параметра «массив1» выделим курсором область ячеек от E5 до E14, которая содержит значения количества клиентов – факторного показателя x;
· после этого наберем в нашей ячейке G3 или в командной строке MS Excel символ «;» (точка с запятой);
· для задания параметра «массив2» выделим курсором область ячеек от D5 до D14, где указаны значения товарооборота туркомпаний – результативного показателя y.
Если все действия были совершены верно, то подстрочная подсказка исчезнет, а в ячейке и в командной строке MS Excel отобразится функция PEARSON с введенными пользователем параметрами (рис. 29).
Убедившись, что параметры команды заданы верно, нажмем на клавишу Enter и увидим (рис. 30), что в выбранной нами ячейке G3 указано значение 0,855074.
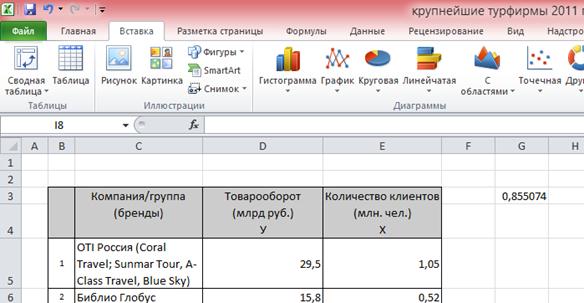
Рис. 30. Иллюстрация результата применения команды PEARSON в MS Excel
Важный момент: если нажать клавишу Enter до момента ввода параметра «массив2» или допустить ошибку при указании диапазонов данных, так что массивы получатся не равными по количеству объектов (например, в параметре «массив1» указать (E5:E14), а в «массив2» – (D6:D13)), то MS Excel вместо результата выведет в выбранной вами ячейке значение «#Н/Д».
Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (результативного признака) обусловлено влиянием одной или нескольких независимых величин (факторных признаков), и в выборе математической модели функции, при помощи которой эту взаимосвязь можно описать. Цель моделирования – получить аналитическое выражение взаимосвязи в виде математической функции, которая позволяет предсказывать значение одной переменной (признака) на основании другой.
Математическую функцию, описывающую зависимость у от х, называют уравнением регрессии, а параметры этой модели – параметрами, или коэффициентами регрессии.
Уравнение регрессии описывает теоретическую линию, вокруг которой концентрируются точки на диаграмме рассеяния и которая определяет основное направление взаимосвязи между признаками x и у. (рис. 31).

Рис. 31. Диаграмма рассеяния (поле корреляции)
Для построения уравнения регрессии необходимо выполнение следующих требований:
· факторный и результативный признаки должны иметь количественное выражение;
· совокупность исходных данных должна быть однородной, значительной по объему и математически описываться непрерывной функцией;
· взаимосвязи между явлениями должны описываться линейной или приводимой к линейной форме зависимостью.
Соблюдение данных требований позволяет построить статистическую модель, наилучшим образом описывающую взаимосвязь между признаками.
Парная линейная регрессия позволяет получить аналитическое выражение связи между двумя признаками – результативным и факторным, описываемое уравнением прямой линии.
Уравнение парной линейной регрессии имеет вид:
![]() , (76)
, (76)
где
![]() – расчетное
значение результативного признака y при определенном значении
факторного признака x;
– расчетное
значение результативного признака y при определенном значении
факторного признака x;
а0 показывает усредненное влияние на результативный признак не учтенных в уравнении факторных признаков;
а1 – коэффициент регрессии, показывающий, насколько в среднем изменится значение результативного признака при изменении факторного на единицу собственного измерения.
Определить тип уравнения можно, исследуя зависимость графически. Существуют другие способы, позволяющие определить вид уравнения связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, между ними существует линейная связь, а при обратной зависимости – гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая, или степенная регрессия.
Оценка параметров уравнения регрессии a0
и a1 осуществляется методом наименьших квадратов. Этот метод
позволяет найти такие параметры модели, при которых расчетные значения ![]() были бы максимально близки к исходным
значениям у. Поскольку в статистке за меру отличия чаще всего
принимается отклонение, то методом наименьших квадратов находятся параметры
модели, при которых минимизируется сумма квадратов отклонений эмпирических
(фактических) значений результативного признака от теоретических, полученных по
линейному уравнению регрессии.
были бы максимально близки к исходным
значениям у. Поскольку в статистке за меру отличия чаще всего
принимается отклонение, то методом наименьших квадратов находятся параметры
модели, при которых минимизируется сумма квадратов отклонений эмпирических
(фактических) значений результативного признака от теоретических, полученных по
линейному уравнению регрессии.
Для нахождения параметров линейной парной регрессии методом наименьших квадратов необходимо решить систему нормальных уравнений, которая имеет следующий вид:
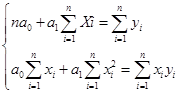 (78)
(78)
где
n – объем исследуемой совокупности (число единиц наблюдения);
xi, уi – значения факторного и результативного признаков у i-й единицы.
Рассчитать параметры линейного уравнения регрессии можно при помощи стандартного табличного редактора MS Excel.
Для начала напомним, что с точки зрения математики линейная функция – это прямая линия, которая проходит в двумерной системе координат. Параметр a0 – это точка, в которой прямая линия пересекает ось y, т.е. в этой точке значение х = 0. За расположение прямой в системе координат отвечает угол наклона прямой линии (отношение величины подъема линии к ее длине), а именно – параметр a1: если наклон имеет знак «+», то линия поднимается слева на право, если наклон равен «0» – линия идет горизонтально оси х, а если знак «-», то линия опускается слева на право.
В MS Excel существует встроенная функция «НАКЛОН», которая позволяет легко получить значение коэффициента a1 по исходным данным y и х методом наименьших квадратов.
Синтаксис этой команды имеет следующий вид:
=НАКЛОН(известные значения_y; известные значения_х) (79)
Параметры команды, указанные в скобочках, задаются пользователем и имеют следующее значение:
Известные значения_y – диапазон данных в исходной таблице, как правило, в столбце, в котором указаны значения результативного показателя y;
Известные значения_х – диапазон данных в исходной таблице, как правило в столбце, в котором указаны значения факторного показателя x.
Диапазоны данных задаются пользователем и очень важно сделать это правильно, поскольку, например, перепутав местами диапазоны х и y, Вы дадите программе команду вычислять коэффициент регрессии уже для другого случая взаимосвязи – исследования влияния значений y на значения х, что не входит в наши планы и неверно, поскольку y будет рассматриваться программой как факторный признак, а не как признак-результат.
Расчет параметра a0 в среде MS Excel также упрощается. Для начала необходимо рассчитать средние значения показателей y и х, вычислить параметр a1, а затем произвести расчет параметра a0 по следующей формуле:
![]() (80)
(80)
Таким образом, расчет параметров уравнения регрессии при помощи MS Excel зависит от точности действий пользователя при вводе исходных данных и задании параметров специальной встроенной для этого команды-функции.
Пример 2. Быстродействие компьютеров, объединенных в сеть, при возникновении перегрузок, как правило, снижается. Естественно, чем больше загрузка компьютера x, тем большим должно быть время реакции y. Под временем реакции понимается интервал с момента нажатия клавиши Enter до момента выдачи компьютером ответа на введенный вами запрос.
Таблица 50.
Показатели быстродействия компьютера
|
Время реакции компьютера, сек. |
Загрузка компьютера от полной его мощности, % |
|
0,31 |
20,2 |
|
0,69 |
22,7 |
|
2,27 |
41,7 |
|
0,57 |
24,6 |
|
1,28 |
20,0 |
|
0,88 |
39,0 |
|
2,11 |
33,4 |
|
4,84 |
63,9 |
|
1,60 |
35,8 |
|
5,06 |
62,3 |
Предположим наличие линейной зависимости между рассматриваемыми показателями. Построим расчетную таблицу для определения параметров линейного уравнения регрессии времени реакции компьютера (табл. 51).
Таблица 51.
Расчетная таблица для определения параметров уравнения регрессии между временем реакции и процентом загрузки компьютера от полной мощности
|
№ п.п. |
Время реакции компьютера (сек), y |
Загрузка компьютера (%), х |
х2 |
xy |
|
|
1. |
0,31 |
20,2 |
408,04 |
6,26 |
0,38 |
|
2. |
0,69 |
22,7 |
515,29 |
15,66 |
0,63 |
|
3. |
2,27 |
41,7 |
1738,89 |
94,66 |
2,53 |
|
4. |
0,57 |
24,6 |
605,16 |
14,02 |
0,82 |
|
5. |
1,28 |
20,0 |
400,00 |
25,60 |
0,36 |
|
6. |
0,88 |
39,0 |
1521,00 |
34,32 |
2,26 |
|
7. |
2,11 |
33,4 |
1115,56 |
70,47 |
1,70 |
|
8. |
4,84 |
63,9 |
4083,21 |
309,28 |
4,75 |
|
9. |
1,60 |
35,8 |
1281,64 |
57,28 |
1,94 |
|
10. |
5,06 |
62,3 |
3881,29 |
315,24 |
4,59 |
|
Итого |
19,61 |
363,6 |
15550,08 |
942,79 |
- |
Система нормальных уравнений для данного примера имеет вид:
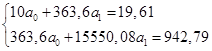
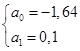
Следовательно, ![]() .
.
Значения ![]() в
таблице 51 получены путем подстановки значений факторного признака хi
(загрузка компьютера) в уравнение регрессии
в
таблице 51 получены путем подстановки значений факторного признака хi
(загрузка компьютера) в уравнение регрессии ![]() .
На рисунке 32 полученные нами расчетные значения
.
На рисунке 32 полученные нами расчетные значения ![]() нанесены
на диаграмму рассеяния, соединены между собой и образуют прямую линию,
обозначающую область концентрации облака точек, построенных по исходным
значениям х и у.
нанесены
на диаграмму рассеяния, соединены между собой и образуют прямую линию,
обозначающую область концентрации облака точек, построенных по исходным
значениям х и у.
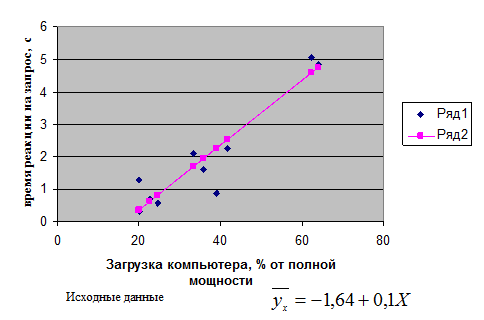
Рис. 32. Зависимость скорости реакции компьютера от состояния его загрузки
Проиллюстрируем расчет параметров линейного уравнения регрессии при помощи МS Excel.
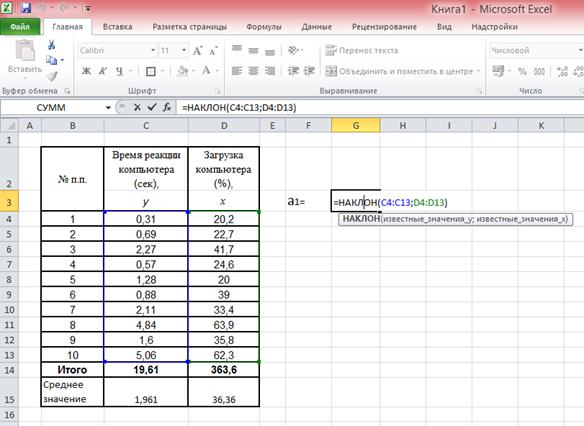
Рис. 33. Иллюстрация применения команды-функции «НАКЛОН» в MS Excel для расчета коэффициента регрессии а1
На рисунке 33 показано, что пользователь рассчитывает значение коэффициента регрессии а1 в ячейке G3. Для этого он предварительно ввел исходные данные в таблицу (столбцы С и D), затем кликнул на ячейку G3, ввел с клавиатуры «=НАКЛОН(», далее, следуя подсказкам Excel, указал известные значения y – это диапазон (С4:С13), затем указал известные значения x – диапазон (D4:D13), после этого ввел с клавиатуры символ «)» (чтобы соблюсти синтаксис команды). Ему остается только нажать клавишу Enter, чтобы увидеть на экране искомое значение коэффициента.
На рис. 34, иллюстрирующем пример расчета коэффициента а0 в MS Excel, видно, что значение коэффициента регрессии а1 – содержимое ячейки G3 – составляет 0,10.
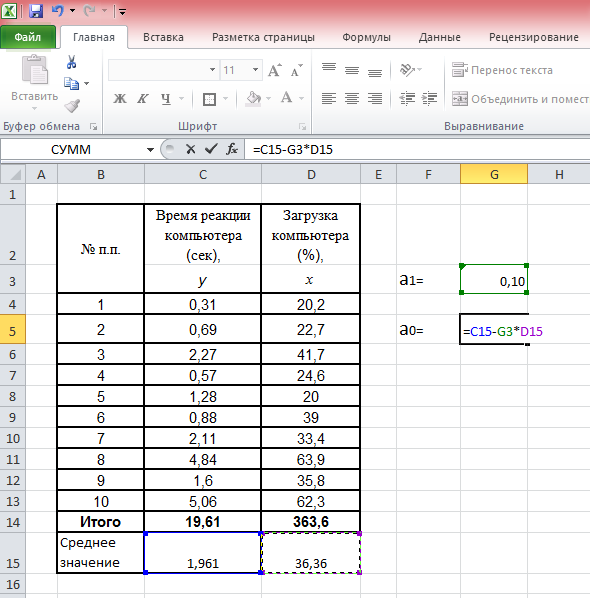
Рис. 34. Иллюстрация расчета параметра а0 в MS Excel после применения команды-функции «НАКЛОН» для расчета коэффициента регрессии а1
Величина а1
необходима для расчета параметра а0 по формуле ![]() . Из рисунка 34. видно, что пользователь
предварительно рассчитал средние значения показателей y и х и перешел к расчету
коэффициента а0 в ячейке G5. Он ввел в эту ячейку символ «=» и согласно формуле задал Excel последовательность действий: «возьми
содержимое ячейки C15 (среднее
значение y), вычти
из него произведение ячейки G3 (коэффициент a1) на
ячейку D15 (среднее значение х)».
Значение коэффициента а0 составляет -1,64, следовательно:
. Из рисунка 34. видно, что пользователь
предварительно рассчитал средние значения показателей y и х и перешел к расчету
коэффициента а0 в ячейке G5. Он ввел в эту ячейку символ «=» и согласно формуле задал Excel последовательность действий: «возьми
содержимое ячейки C15 (среднее
значение y), вычти
из него произведение ячейки G3 (коэффициент a1) на
ячейку D15 (среднее значение х)».
Значение коэффициента а0 составляет -1,64, следовательно: ![]()
Коэффициент регрессии a1 = 0,1 означает, что при увеличении загрузки компьютерных мощностей на 1 % время реакции компьютера повышается в среднем на 0,1 сек.
Данную оценку связи можно
использовать для прогнозирования времени реакции компьютера при
соответствующем проценте загрузке. Например, при загрузке компьютера на 50 %
время его реакции составит ![]() сек.
сек.
Линейные модели являются основными при определении аналитического выражения связи. Однако встречаются и нелинейные связи, хорошо описываемые параболой, гиперболой и т.д. Если связь между факторным и результативным признаками описывается уравнением параболы второго порядка вида:
![]() , (81)
, (81)
то система нормальных уравнений имеет вид:
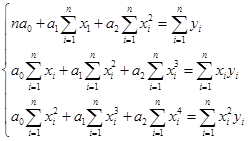 (82)
(82)
Оценка обратной связи осуществляется на основании гиперболы вида:
![]() (83)
(83)
Система нормальных уравнений для нахождения параметров гиперболы:
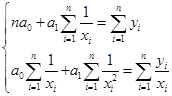 (84)
(84)
При нелинейной зависимости между признаками для измерения тесноты связи между ними вычисляют теоретическое корреляционное отношение:
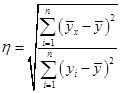 (85)
(85)
Корреляционное отношение
изменяется в пределах от 0 до 1 ![]() .
Его величина интерпретируется по стандартным критериям оценки коэффициента
корреляции.
.
Его величина интерпретируется по стандартным критериям оценки коэффициента
корреляции.
Пример 3. Рассмотрим данные об объеме производства вишни в фермерских хозяйствах и цене вишни.
Таблица 52.
Объем производства и фермерская цена вишни хозяйств области
|
№ п/п |
Объем производства, тыс. т |
Фермерская цена, тыс. долл. за т |
|
1. |
0,204 |
0,267 |
|
2. |
0,260 |
0,174 |
|
3. |
0,287 |
0,140 |
|
4. |
0,239 |
0,208 |
|
5. |
0,208 |
0,225 |
|
6. |
0,218 |
0,243 |
|
7. |
0,394 |
0,227 |
|
8. |
0,266 |
0,166 |
|
9. |
0,276 |
0,163 |
|
10. |
0,404 |
0,262 |
|
11. |
0,331 |
0,126 |
|
12. |
0,373 |
0,165 |
|
13. |
0,200 |
0,299 |
|
14. |
0,198 |
0,325 |
|
15. |
0,356 |
0,150 |
|
16. |
0,384 |
0,188 |
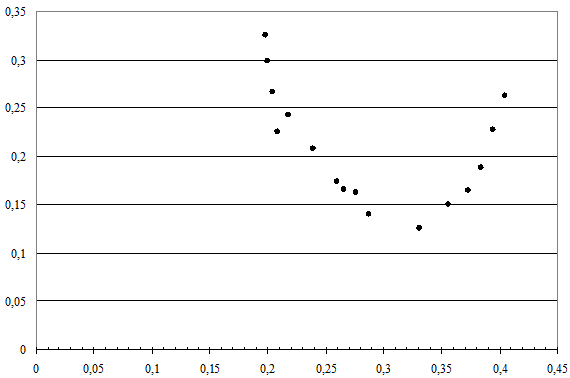
Рис. 35. Диаграмма рассеяния, характеризующая взаимосвязь между объемом производства вишни и фермерской ценой на нее
Таблица 53.
Расчетная таблица для нахождения параметров уравнения регрессии
|
Объем производства, тыс. т, xi |
Фермерская цена, тыс. долл. за т, yi |
хi2 |
хi3 |
хi4 |
xiyi |
хi2yi |
|
|
0,204 |
0,267 |
0,042 |
0,008 |
0,002 |
0,054 |
0,011 |
0,234 |
|
0,260 |
0,174 |
0,068 |
0,018 |
0,005 |
0,045 |
0,012 |
0,221 |
|
0,287 |
0,140 |
0,082 |
0,024 |
0,007 |
0,040 |
0,012 |
0,213 |
|
0,239 |
0,208 |
0,057 |
0,014 |
0,003 |
0,050 |
0,012 |
0,226 |
|
0,208 |
0,225 |
0,043 |
0,009 |
0,002 |
0,047 |
0,010 |
0,233 |
|
0,218 |
0,243 |
0,048 |
0,010 |
0,002 |
0,053 |
0,012 |
0,231 |
|
0,394 |
0,227 |
0,155 |
0,061 |
0,024 |
0,089 |
0,035 |
0,177 |
|
0,266 |
0,166 |
0,071 |
0,019 |
0,005 |
0,044 |
0,012 |
0,219 |
|
0,276 |
0,163 |
0,076 |
0,021 |
0,006 |
0,045 |
0,012 |
0,216 |
|
0,404 |
0,262 |
0,163 |
0,066 |
0,027 |
0,106 |
0,043 |
0,174 |
|
0,331 |
0,126 |
0,110 |
0,036 |
0,012 |
0,042 |
0,014 |
0,200 |
|
0,373 |
0,165 |
0,139 |
0,052 |
0,019 |
0,061 |
0,023 |
0,185 |
|
0,200 |
0,299 |
0,040 |
0,008 |
0,002 |
0,060 |
0,012 |
0,235 |
|
0,198 |
0,325 |
0,039 |
0,008 |
0,002 |
0,064 |
0,013 |
0,235 |
|
0,356 |
0,150 |
0,127 |
0,045 |
0,016 |
0,053 |
0,019 |
0,191 |
|
0,384 |
0,188 |
0,147 |
0,056 |
0,022 |
0,072 |
0,028 |
0,181 |
|
4,5979 |
3,328 |
1,407 |
0,455 |
0,154 |
0,927 |
0,278 |
3,371 |
Система нормальных уравнений для данного примера имеет вид (согласно формуле 82):
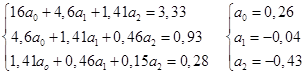
Следовательно, ![]() .
.
Значения ![]() в
таблице 53 получены путем пошаговой подстановки значений факторного признака хi
(объем производства вишни) в уравнение регрессии. Коэффициент регрессии a1 = -0,04
означает, что при увеличении объема производства вишни на 1 тыс. т
фермерская цена будет в среднем снижаться на 0,04 тыс. долл.
в
таблице 53 получены путем пошаговой подстановки значений факторного признака хi
(объем производства вишни) в уравнение регрессии. Коэффициент регрессии a1 = -0,04
означает, что при увеличении объема производства вишни на 1 тыс. т
фермерская цена будет в среднем снижаться на 0,04 тыс. долл.
Определим тесноту связи между объемом производства и фермерской ценой вишни. Все расчеты представим во вспомогательной табл. 54.
Таблица 54.
Расчетная таблица для определения теоретического корреляционного отношения
|
yi |
|
|
|
|
|
|
0,267 |
0,234 |
0,026 |
0,067 |
0,059 |
0,348 |
|
0,174 |
0,221 |
0,013 |
0,016 |
-0,034 |
0,116 |
|
0,140 |
0,213 |
0,005 |
0,003 |
-0,068 |
0,462 |
|
0,208 |
0,226 |
0,018 |
0,032 |
0,000 |
0,000 |
|
0,225 |
0,233 |
0,025 |
0,063 |
0,017 |
0,029 |
|
0,243 |
0,231 |
0,023 |
0,052 |
0,035 |
0,123 |
|
0,227 |
0,177 |
-0,030 |
0,093 |
0,019 |
0,036 |
|
0,166 |
0,219 |
0,011 |
0,012 |
-0,042 |
0,176 |
|
0,163 |
0,216 |
0,008 |
0,006 |
-0,045 |
0,203 |
|
0,262 |
0,174 |
-0,030 |
0,119 |
0,054 |
0,292 |
|
0,126 |
0,200 |
-0,010 |
0,010 |
-0,082 |
0,672 |
|
0,165 |
0,185 |
-0,020 |
0,051 |
-0,043 |
0,185 |
|
0,299 |
0,235 |
0,027 |
0,072 |
0,091 |
0,828 |
|
0,325 |
0,235 |
0,027 |
0,074 |
0,117 |
1,369 |
|
0,150 |
0,191 |
-0,020 |
0,028 |
-0,058 |
0,336 |
|
0,188 |
0,181 |
-0,030 |
0,071 |
-0,020 |
0,040 |
|
Итого |
- |
0,766 |
- |
5,215 |
|
Теоретическое корреляционное отношение согласно формуле 85 составит:
![]()
Таким образом, связь между объемом производства вишни и фермерской ценой можно признать умеренной. Невысокое значение теоретического корреляционного отношения в данном случае оправдано, поскольку кроме объема производства на устанавливаемую фермерами цену оказывают сильное влияние другие факторы (уровень производственных издержек, конъюнктура спроса, цены конкурентов и др.).
Интерпретация моделей регрессии начинается со статистической оценки уравнения регрессии в целом и оценки входящего в модель факторного признака. Прежде всего, необходимо оценить коэффициенты регрессии. Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый.
Знаки коэффициентов регрессии говорят о характере влияния на результативный признак. Если коэффициент регрессии при факторном признаке имеет знак «плюс», то с увеличением данного фактора результативный признак возрастает; если знак «минус», то с ростом значений этого факторного признака значения результативного признака уменьшаются.
Если экономические процессы подсказывают, что факторный признак должен иметь положительное значение, а он имеет знак «минус», то необходимо проверить расчеты параметров уравнения регрессии. Такое явление чаще всего бывает в силу допущенных ошибок при вычислении.
С целью расширения возможностей экономического анализа используются коэффициенты эластичности, определяемые по формуле:
![]() , (86)
, (86)
где
![]() – среднее
значение соответствующего факторного признака;
– среднее
значение соответствующего факторного признака;
![]() – среднее
значение результативного признака;
– среднее
значение результативного признака;
a1 – коэффициент регрессии при соответствующем факторном признаке.
Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1 %.
Пример 4. Определим коэффициент эластичности по данным примера 73.
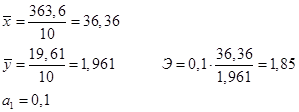
Таким образом, при увеличении загрузки мощности компьютера на 1 % время реакции соответственно увеличится на 1,85 %.
1. Что можно сказать о связи, если линейный коэффициент корреляции равен:
а) нулю;
б) единице;
в) -0,15?
2. Если вы выявили сильную положительную корреляцию, говорит ли это о том, что большие значения факторного признака вызывают появление больших значений результативного? Если нет, какие еще возможны варианты?
3. Что представляют собой параметры «массив1» и «массив2» при расчете линейного коэффициента корреляции Пирсона в MS Excel?
4. Какие требования к исходным данным важно соблюдать, приступая к расчету коэффициента корреляции в MS Excel?
5. В чем состоят особенности применения регрессионного анализа?
6. Если результативный и факторный признак имеют тенденцию к стабильному росту, то какой аналитической функцией описывается взаимосвязь между ними?
7. Что характеризует коэффициент регрессии в уравнении связи и важно ли учитывать его знак?
8. Что показывает коэффициент эластичности?
9. Какой показатель используется для оценки тесноты связи между x и y при существовании между ними нелинейной зависимости?
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Задание 1.
Какой метод анализа – корреляционный или регрессионный – следует применить в каждой из описанных ниже ситуаций?
|
Ситуация для анализа |
Метод статистического анализа |
|
1. Выявление наличия взаимосвязи между расходами на рекламу и объемом продаж. |
· Корреляционный; · Регрессионный. |
|
2. Прогнозирование объема выпуска продукции на основании величины капитальных вложений. |
· Корреляционный; · Регрессионный. |
|
3. Прогнозирование вероятности банкротства предприятия на основании показателей использования активов и величины финансовых обязательств. |
· Корреляционный; · Регрессионный. |
|
4. Анализ данных с целью определения силы влияния морально-психологического состояния работников на их производительность. |
· Корреляционный; · Регрессионный. |
|
5. Анализ влияния потребительских ожиданий на изменение котировок финансового актива. |
· Корреляционный; · Регрессионный. |
Задание 2.
По данным авто.ru о предложении на продажу автомобиля с пробегом марки Volvo S60 c двигателем «турбодизель» определите, какой из показателей «срок эксплуатации» или «пробег» в большей степени оказывает влияние на цену продажи. Постройте уравнение регрессии между показателем «цена продажи» и наиболее сильно влияющим на него показателем. Интерпретируйте полученное значение коэффициента регрессии при факторном признаке.
|
№ п.п. |
Цена продажи, млн руб. |
Срок эксплуатации, лет |
Пробег, тыс. км. |
|
|
|
|
|
|
1. |
1,05 |
3 |
75 |
|
|
|
|
|
|
2. |
1,04 |
3 |
70 |
|
|
|
|
|
|
3. |
1,07 |
2 |
68 |
|
|
|
|
|
|
4. |
1,10 |
3 |
61 |
|
|
|
|
|
|
5. |
1,16 |
3 |
58 |
|
|
|
|
|
|
6. |
1,25 |
3 |
55 |
|
|
|
|
|
|
7. |
1,25 |
2 |
39 |
|
|
|
|
|
|
8. |
1,32 |
1 |
12 |
|
|
|
|
|
|
Итого: |
|
|
|
|
|
|
|
|
|
Среднее значение: |
|
|
|
|
|
|
|
|
Задание 3.
Определите вид корреляционной зависимости, рассчитайте значение коэффициента корреляции, постройте уравнение регрессии между объемом реализованной продукции и балансовой прибылью 10 предприятий одной из отраслей промышленности. Интерпретируйте полученные значения показателей.
|
Номер предприятия |
Объем реализованной продукции, млрд руб. |
Балансовая прибыль, млрд руб. |
|
|
|
|
1. |
491,8 |
133,8 |
|
|
|
|
2. |
483,0 |
124,1 |
|
|
|
|
3. |
461,7 |
62,4 |
|
|
|
|
4. |
478,7 |
100,9 |
|
|
|
|
5. |
476,9 |
88,4 |
|
|
|
|
6. |
475,2 |
72,4 |
|
|
|
|
7. |
474,4 |
99,3 |
|
|
|
|
8. |
459,5 |
40,9 |
|
|
|
|
9. |
462,9 |
104,0 |
|
|
|
|
10. |
456,5 |
66,1 |
|
|
|
|
Итого: |
|
|
|
|
|
|
Среднее значение: |
|
|
|
|
|
Цель изучения темы состоит в формировании системы знаний и компетенций о методах анализа, расчета и интерпретации статистических показателей, применяемых для анализа развития социально-экономических явлений и процессов во времени и построения теоретических моделей для предсказания развития этих явлений и процессов в будущие периоды.
В результате успешного освоения темы Вы:
Узнаете:
· что такое «ряд динамики» и какими параметрами он характеризуется;
· по каким признакам классифицируются ряды динамики;
· что такое сопоставимость данных и как можно ее обеспечить;
· как оценивать и анализировать развитие явлений во времени и какие показатели для этого нужно использовать;
· что такое средняя скорость и интенсивность развития явления и как рассчитывать средние аналитические показатели динамики;
· что такое тенденция и тренд ряда динамики;
· какие методы применяют для выявления тенденции в рядах динамики;
· как осуществляется сглаживание и выравнивание уровней ряда;
· что такое уравнение тренда и какими способами можно рассчитать его параметры;
· что такое экстраполяция тренда и для чего она используется;
· основные методы простейшего прогнозирования временных рядов.
Приобретете компетенции:
· владение методами количественного анализа и моделирования, теоретического и экспериментального исследования;
· владение основными методами, способами и средствами получения, хранения, переработки информации, навыками работы с компьютером как средством управления информацией;
· способность оценивать воздействие макроэкономической среды на функционирование организаций и органов государственного и муниципального управления;
· умение применять количественные и качественные методы анализа при принятии управленческих решений и строить экономические, финансовые и организационно-управленческие модели;
· способность анализировать финансовую отчетность и принимать обоснованные инвестиционные, кредитные и финансовые решения;
· способность оценивать эффективность использования различных систем учета и распределения затрат и принимать обоснованные управленческие решения на основе данных управленческого учета;
· способность строить ряды динамики и оформлять результаты в виде таблиц;
· способность рассчитывать абсолютные, относительные и средние показатели динамики и анализировать их значения;
· способность выявлять основную тенденцию развития ряда динамики различными методами;
· способность выбирать и рассчитывать параметры функции, описывающей закономерность развития ряда динамики;
· способность прогнозировать развитие ряда динамики.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· ряд динамики и его компоненты;
· моментные и интервальные ряды динамики;
· равноотстоящие и неравноотстоящие ряды динамики;
· смыкание рядов динамики;
· абсолютный прирост;
· темп роста;
· темп прироста;
· средний уровень ряда;
· средний абсолютный прирост;
· средний темп роста;
· средний темп прироста;
· тенденция;
· аналитическое выравнивание и механическое выравнивание (сглаживание);
· скользящая средняя;
· центрирование;
· аналитическое выравнивание;
· тренд и уравнение тренда;
· метод наименьших квадратов;
· метод условного нуля;
· экстраполяция.
Вопросы темы:
1. Понятие и классификация рядов динамики.
2. Аналитические показатели динамики.
3. Тенденция ряда динамики и методы ее выявления.
4. Простейшие методы прогнозирования.
Теоретический материал по теме
Процессы изменения социально-экономических явлений во времени в статистике называют динамикой. Для отображения динамики строят особые ряды статистических показателей – ряды динамики.
Ряд динамики (временной ряд, time series) – это последовательность изменяющихся во времени значений показателя, расположенных в хронологическом порядке.
Составными элементами ряда динамики являются: значения показателя – уровни ряда и периоды (годы, кварталы, месяцы, сутки) или моменты (даты) времени. Уровни ряда обычно обозначаются через y, моменты или периоды времени, к которым относятся уровни, – через t.
Ряды динамики, как правило, представляют в виде таблицы и/или диаграммы динамики. Классификация рядов динамики представлена на рис. 36.
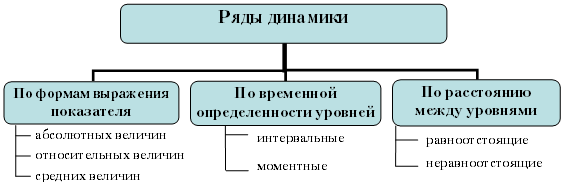
Рис. 36. Классификация рядов динамики
Ряд динамики абсолютных величин представлен в первой строке таблицы 55, ряд средних величин – в 3-й строке; ряд относительных величин – во 2-й строке.
Число построенных квартир и их средний размер в РФ
|
|
2008 |
2009 |
2010 |
2011 |
2012 |
|
Число квартир, тыс. |
768 |
702 |
717 |
786 |
838 |
|
Число однокомнатных квартир, % от общего количества |
33 |
33 |
34 |
36 |
38 |
|
Средний размер квартир, м2 общей площади |
83,4 |
85,3 |
81,5 |
79,3 |
78,4 |
Уровни моментных рядов динамики характеризуют явление по состоянию на определенный момент времени (табл. 56).
Численность персонала фирмы в I полугодии 2013 г.
(на 1-е число месяца)
|
Дата |
1.01 |
1.02 |
1.03 |
1.04 |
1.05 |
1.06 |
|
Численность персонала, чел. |
780 |
810 |
880 |
930 |
940 |
970 |
Уровни моментных рядов абсолютных величин нельзя суммировать, так как в них повторяются одни и те же единицы совокупности.
Ряд, в котором уровни характеризуют результат, накопленный или вновь произведенный за определенный интервал времени, называется интервальным рядом (табл. 57).
Динамика объема розничного товарооборота в регионе
|
Месяц |
Январь |
Февраль |
Март |
Апрель |
Май |
Июнь |
|
Товарооборот, млн руб. |
3,4 |
3,2 |
3,6 |
3,8 |
3,5 |
3,7 |
В отличие от моментных рядов, сумма уровней интервального ряда является реальным показателем, например, общий объем розничного товарооборота за I полугодие (с января по июнь).
Ряды динамики следующих друг за другом периодов или повторяющихся через равные промежутки дат называются равноотстоящими. Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются неравноотстоящими.
Важнейшим условием правильного построения рядов динамики является сопоставимость входящих в него уровней, под которой понимается соответствие всех уровней ряда динамики:
· единым единицам измерения и единицам счета;
· единой методологии учета и расчета показателей;
· единым административным и территориальным границам.
Чтобы привести уровни ряда динамики к сопоставимому виду, используют прием, который носит название смыкание рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики с несопоставимыми уровнями. Для смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах). По такому уровню рассчитывают соотношение значений показателя – коэффициент пересчета и все остальные уровни умножаются на значение коэффициента. Другой способ смыкания рядов заключается в том, что уровни года, в котором произошли изменения принимаются за 100 %, а остальные пересчитываются в процентах по отношению к этим уровням соответственно.
При сравнительном анализе развития во времени экономических показателей стран, административных и территориальных районов ряды динамики приводятся к одному основанию – к одному периоду или моменту времени, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.
Для количественной оценки развития явлений во времени используются аналитические показатели динамики. Они характеризуют в абсолютном или относительном выражении как изменилось значение показателя в одном уровне рассматриваемого ряда динамики по сравнению с другим уровнем. При этом сравниваемый уровень называют текущим, или отчетным, а уровень, с которым происходит сравнение – базисным.
Поскольку время развивается всегда однонаправлено, каждый уровень ряда динамики можно сравнить с предшествующим или с другим, более ранним уровнем, выбранным за базу сравнения (как правило, первым в ряду). В первом случае рассчитанные аналитические показатели называют цепными, а при сравнении всех уровней ряда с фиксированным уровнем – базисными (рис. 37).
Рис. 37. Построение цепных и базисных аналитических показателей динамики
К основным аналитическим индивидуальным показателям динамики относятся: абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста (табл. 58).
Таблица 58.
Индивидуальные аналитические показатели динамики
|
Название и обозначение показателя |
Содержание показателя |
Формула расчета |
|
|
Цепные показатели |
Базисные показатели |
||
|
Абсолютный прирост
|
Показывает, на сколько единиц измерения выросло или сократилось значение уровня в текущем периоде по сравнению с предшествующим или выбранным за базу сравнения. |
|
|
|
Темп роста Тр |
В долях единицы (коэффициентах). Показывает, во сколько раз данный уровень ряда больше предшествующего или базисного уровня. В процентах. Показывает, сколько процентов составляет величина уровня в текущем периоде от его величины в предшествующем или выбранном за базу сравнения периоде. |
|
|
|
Темп прироста Тпр |
Показывает, на сколько процентов изменился сравниваемый уровень по отношению к предшествующему уровню или принятому за базу сравнения. |
|
|
|
Абсолютное значение одного процента прироста |%| |
Показывает сколько абсолютных единиц приходится на 1 % прироста значения уровня в текущем периоде по сравнению с предшествующим. |
|
- |
|
Обозначения: yi – рассматриваемый уровень ряда динамики – текущий уровень; yi–1 – уровень ряда, предшествующий текущему; y1 – начальный уровень ряда динамики (или принятый за базу сравнения). |
|||
Для обобщения данных об изменении уровней ряда динамики рассчитываются средние аналитические показатели динамики, к которым относятся: средний уровень ряда; средний абсолютный прирост; средний темп роста; средний темп прироста.
Формулы для расчета среднего уровня ряда приведены в табл. 59. Примеры расчета среднего уровня в моментных рядах динамики рассмотрены в теме 5 (вопрос 4, Средняя хронологическая).
Таблица 59.
Расчет среднего уровня ряда динамики
|
Название и обозначение показателя |
Содержание показателя |
Формула расчета |
|
|
Для рядов с равноотстоящими уровнями |
Для рядов с неравноотстоящими уровнями |
||
|
Средний уровень ряда |
Характеризует средний размер уровня в каждый период или момент времени в течение рассмотренного временного интервала |
Для интервальных рядов динамики |
|
|
|
|
||
|
Для моментных рядов динамики |
|||
|
|
|
||
|
Обозначения: yi – значения уровней рассматриваемого ряда динамки; n – число уровней ряда; y1 – начальный уровень ряда динамики; ti – продолжительность интервалов времени между уровнями; (число периодов времени, в которых значение уровня не изменялось). |
|||
Расчет остальных средних аналитических показателей осуществляется по формулам таблицы 60.
Таблица 60.
Средние аналитические показатели динамики
|
Название и обозначение показателя |
Содержание показателя |
Формула расчета |
|
Средний абсолютный прирост |
Показывает, на сколько единиц измерения в среднем вырастало или сокращалось значение показателя от уровня к уровню в течение рассмотренного периода динамики. |
|
|
Средний темп роста |
В долях единицы (коэффициентах). Показывает, во сколько раз в среднем возрастало или сокращалось значение показателя от уровня к уровню в течение рассмотренного периода динамики.
В процентах. Показывает, сколько в среднем процентов последующий уровень составляет от предыдущего в течение всего периода динамики. |
Для рядов с равноотстоящими уровнями
Для рядов с неравноотстоящими уровнями
|
|
Средний темп прироста |
Показывает, на сколько процентов в среднем возрастала или сокращалась величина показателя от уровня к уровню в течение рассмотренного периода динамики. |
|
|
Обозначения: yi – рассматриваемый уровень ряда динамики – текущий уровень; yi–1 – уровень ряда, предшествующий текущему; y1 – начальный уровень ряда динамики; ti – продолжительность интервалов времени между уровнями; (число периодов времени, в которых значение уровня не изменялось); К – соответствующий коэффициент роста – темп роста, выраженный в долях единицы. |
||
Средний абсолютный прирост является обобщающим показателем абсолютной скорости изменения явления во времени, а средний темп роста оценивает среднюю интенсивность изменения уровней ряда динамики.
Пример 1. По данным об объеме экспорта РФ со странами дальнего зарубежья за 2007–2011 гг. рассчитаем аналитические показатели ряда динамики (табл. 61.).
1. Рассчитаем цепные (гр. 2 табл. 61) и базисные (гр. 3 табл. 61) абсолютные приросты:
Цепные (по сравнению с предшествующим годом):
![]()
![]()
![]()
![]()
Таблица 61.
Объем экспорта РФ со странами дальнего зарубежья в 2007–2011 гг. (млрд долл. США)
|
Год |
Объем |
Абсолютный прирост, |
Темп роста, % |
Темп прироста, % |
Абсолютное |
|||
|
по сравн. |
по сравн. |
по сравн. |
по сравн. |
по сравн. |
по сравн. |
|||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
2007 |
300,0 |
- |
- |
- |
- |
- |
- |
- |
|
2008 |
400,0 |
100,0 |
100,0 |
133,33 |
133,33 |
33,33 |
33,33 |
3,000 |
|
2009 |
255,0 |
-145,0 |
-45,0 |
63,75 |
85,00 |
-36,25 |
-15,00 |
4,000 |
|
2010 |
338,0 |
83,0 |
38,0 |
132,55 |
112,67 |
32,55 |
12,67 |
2,550 |
|
2011 |
438,0 |
100,0 |
138,0 |
129,59 |
146,00 |
29,59 |
46,00 |
3,380 |
|
Итого |
1731,0 |
138,0 |
- |
- |
- |
- |
- |
- |
Базисные (по сравнению с 2007 г.):
![]()
![]()
![]()
![]()
2. Рассчитаем цепные (гр. 4) и базисные (гр. 5) темпы роста:
Цепные (по сравнению с предшествующим годом):
![]()
![]()
![]()
![]()
Базисные (по сравнению с 2007 годом):
![]()
![]()
![]()
![]()
3. Рассчитаем цепные (гр. 6) и базисные (гр. 7) темпы прироста:
Цепные (по сравнению с предшествующим годом):
Тпр08/07 = 133,33 % – 100 % = 33,33 %
Тпр09/08 =63,75 % – 100 % = -36,25 %
Тпр 10/09 =132,55 % – 100 % = 32,55 %
Тпр 11/10 =129,59 % – 100 % = 29,59 %
Базисные (по сравнению с 2007 годом):
Тпр 08/07 = 133,33 % – 100 % = 33,33 %
Тпр 09/07 =85,00 % – 100 % = -15,00 %
Тпр 10/07 =112,67 % – 100 % = 12,67 %
Тпр 11/07 =146,00 % – 100 % = 46,00 %
4. Рассчитаем абсолютное значение одного процента прироста (гр. 8):
|%|2008 = у2007 * 0,01 =300,0 * 0,01 = 3,000 млрд долл. США
|%|2009 = у 2008 * 0,01 =400,0 * 0,01 = 4,000 млрд долл. США
|%|2010 = у 2009 * 0,01 =255,0 * 0,01 = 2,550 млрд долл. США
|%|2011 = у 2010 * 0,01 =338,0 * 0,01 = 3,380 млрд долл. США
5. Рассчитаем среднегодовой объем экспорта РФ в страны дальнего зарубежья за 2007–2011 гг. Рассматриваемый ряд динамики является интервальным рядом с равноотстоящими уровнями, поэтому используем формулу средней арифметической простой:
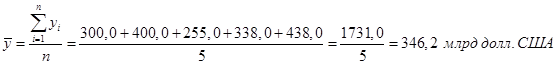
т.е. в среднем в период с 2007 по 2011 г. РФ ежегодно экспортировала в страны дальнего зарубежья товаров на сумму 346,2 млрд руб.
6. Определим средний абсолютный прирост объема экспорта РФ в страны дальнего зарубежья в 2007–2011 гг. Он составит:
![]()
Это означает, что в среднем за 2007–2011 гг. объем экспорта РФ в страны дальнего зарубежья ежегодно возрастал на 34,5 млрд долл. США.
7. Рассчитаем средний темп роста объема экспорта РФ в страны дальнего зарубежья в 2007–2011 гг.
![]()
![]()
Таким образом, в среднем объем экспорта РФ в страны дальнего зарубежья в период с 2007 по 2011 г. ежегодно возрастал в 1,0992 раза.
8. Найдем значение среднего темпа прироста. Поскольку средний темп роста объема экспорта РФ в страны дальнего зарубежья в 2007–2011 гг. составил 109,92 %, отсюда средний темп прироста будет равен:
![]()
Соответственно, в течение 2007–20011 гг. объем экспорта РФ в страны дальнего зарубежья в среднем ежегодно возрастал на 9,92 %.
Под основной тенденцией развития ряда динамики понимают изменение, определяющее общее направление развития. Для выявления основной тенденции развития в статистике применяются две группы методов (рис. 38):
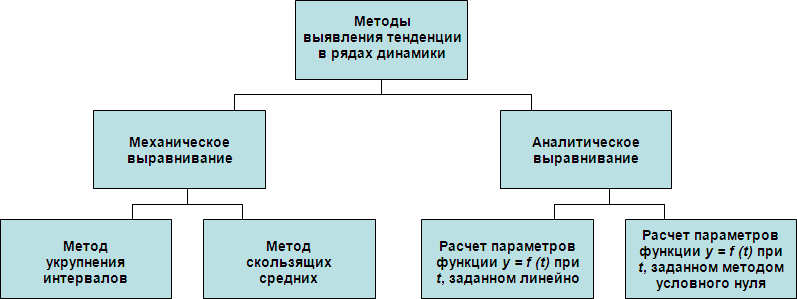
Рис. 38. Методы выявления тенденции в рядах динамики
Аналитическое выравнивание основано на расчете теоретических значений уровня ряда по наиболее подходящей модели их изменения. Модель представляет собой уравнение функции, позволяющей получить значения уровней ряда на основании значений фактора времени y = f(t). График теоретических значений образует линию, проведенную между конкретными уровнями ряда таким образом, чтобы она отражала тенденцию, присущую ряду, и одновременно освободила его от незначительных колебаний.
Механическое выравнивание (сглаживание) уровней ряда динамики осуществляется с использованием фактических значений соседних уровней. В результате получается новый ряд динамики, в котором колебания уровней в значительной мере погашены и основная тенденция развития этого ряда проступает более наглядно.
Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни. Например, ряд недельных данных можно преобразовать в ряд помесячной динамики, ряд квартальных данных заменить годовыми уровнями. Уровни нового ряда могут быть получены путем суммирования уровней исходного ряда либо могут представлять средние значения, рассчитанные по соответствующим уровням.
Метод скользящей средней. Выравнивание или сглаживание ряда динамики методом скользящих средних сводится к замене фактических уровней ряда расчетными уровнями, которые в меньшей степени подвержены колебаниям, что способствует более четкому проявлению тенденции развития. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем средний уровень из такого же числа уровней начиная со второго, далее – начиная с третьего и т.д. Таким образом, при расчете средних уровней они как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень вначале и добавляя один следующий. Отсюда название – скользящая средняя.
Каждое звено скользящей средней – это средний уровень за соответствующий период, который относится к середине выбранного периода, если число уровней ряда динамики нечетное.
Нахождение скользящей средней по четному числу уровней ряда динамики несколько сложнее, так как средняя может быть отнесена только к середине между двумя датами, находящимся в середине интервала сглаживания. Например, средняя, найденная для четырех первых уровней, относится к середине между вторым и третьим уровнями, средняя из значений показателя, стоящих в ряду динамики на втором, третьем, четвертом и пятом местах, придется на середину между третьим и четвертым уровнями, и так далее. Чтобы ликвидировать такой сдвиг, применяют способ центрирования. Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенной дате. Для этого необходимо найти скользящие суммы, затем по этим суммам рассчитать скользящие средние нецентрированные и после этого произвести центрирование – последовательно найти средние арифметические значения из соседних нецентрированных скользящих средних.
Пример 2. Покажем расчет скользящих средних за 3 и 4 месяца по данным, представленным в таблице 62.
Таблица 62.
Объем оказанных платных услуг населению региона за 2012 г.
|
Месяц |
Объем оказан- ных услуг, млн руб. |
Трехуровневые скользящие суммы |
Трехуровневые скользящие средние |
Четырехуров-невые скользящие суммы |
Четырехуровневые скользящие средние нецентри- рованные |
Четырехуровневые скользящие средние центриро- ванные |
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
|
январь |
13,3 |
- |
- |
- |
|
- |
|
февраль |
13,4 |
- |
13,40 |
- |
|
- |
|
март |
13,5 |
40,2 |
13,43 |
- |
|
13,44 |
|
апрель |
13,4 |
40,3 |
13,50 |
53,6 |
13,40 |
13,53 |
|
май |
13,6 |
40,5 |
13,60 |
53,9 |
13,48 |
13,64 |
|
июнь |
13,8 |
40,8 |
13,80 |
54,3 |
13,58 |
13,80 |
|
июль |
14,0 |
41,4 |
14,00 |
54,8 |
13,70 |
13,96 |
|
август |
14,2 |
42,0 |
14,10 |
55,6 |
13,90 |
14,08 |
|
сентябрь |
14,1 |
42,3 |
14,17 |
56,1 |
14,03 |
14,16 |
|
октябрь |
14,2 |
42,5 |
14,20 |
56,5 |
14,13 |
14,23 |
|
ноябрь |
14,3 |
42,6 |
14,30 |
56,8 |
14,20 |
- |
|
декабрь |
14,4 |
42,9 |
- |
57,0 |
14,25 |
- |
В результате расчета трехуровневых скользящих средних получен новый ряд значений объема оказанных услуг (графа 3 табл. 62), представленный на рисунке 39 а). Поскольку рассчитанные трехуровневые средние значения возрастают, то ряд динамики объема оказанных платных услуг населению имеет общую тенденцию к росту. Тенденция к росту отчетливо видна также и на графике.
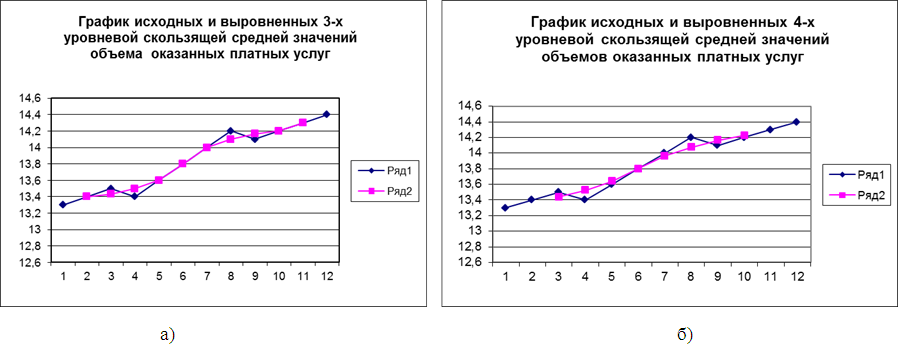
Рис. 39. Графики динамики исходных и выровненных 3- и 4-уровневой скользящими средними значений объема оказанных платных услуг населению региона по месяцам 2012 г.
где
Ряд 1 – исходные данные;
Ряд 2 – значения соответствующих скользящих средних.
Анализ значений четырехуровневых скользящих средних (графа 6 табл.62), изображенных на графике 39 б), также подтверждает наличие в ряду динамики объема оказанных платных услуг населению тенденции к росту.
Недостаток метода простой скользящей средней состоит в том, что сглаженный ряд динамики сокращается ввиду невозможности получить сглаженные уровни для начала и конца ряда. Этот недостаток устраняется применением метода аналитического выравнивания для анализа основной тенденции.
Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени: = f(t).
При таком подходе изменение явления связывают лишь с течением времени; считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени.
Для отображения основной тенденции развития явлений во времени применяются различные функции: полиномы разной степени, экспоненты, логистические кривые и другие виды.
Полиномы имеют следующий вид:
полином
первой степени: ![]() ,
,
полином
второй степени: ![]() , (87)
, (87)
полином
третьей степени: ![]() ,
,
полином
n-ой степени: ![]() .
.
Здесь a0; a1; a2; … an – параметры полиномов, t – условное обозначение времени. В статистической практике параметры полиномов невысокой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, например, параметр a0 характеризует средние условия развития ряда динамики, параметр a1 – скорость роста, параметр a2 – ускорение роста, параметр а3 – изменение ускорения.
Оценка параметров в моделях 87 находится методом наименьших квадратов. Как известно, суть его состоит в определении таких параметров (коэффициентов), при которых сумма квадратов отклонений расчетных значений уровней от фактических значений была бы минимальной. Таким образом, эти оценки находятся в результате минимизации выражения:
![]() (88)
(88)
где:
yt – фактическое значение уровня ряда динамики;
![]() – расчетное значение;
– расчетное значение;
n – количество уровней в ряду динамики.
Тогда система нормальных
уравнений для оценивания параметров прямой ![]() имеет
вид:
имеет
вид:
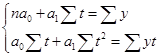 (89)
(89)
Для параболы второго порядка (yt = a0 + a1 t + a2 t2):
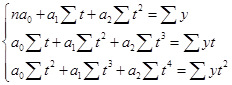 (90)
(90)
Закономерность, согласно которой
изменяются значения уровней ряда динамики, в статистике принято называть трендом,
а математическое выражение функции, описывающей это изменение – уравнением
тренда. Так, например, рассчитав параметры прямой ![]() ,
говорят: уравнение тренда по модели прямой имеет вид: уt = 28 + 2,3t.
,
говорят: уравнение тренда по модели прямой имеет вид: уt = 28 + 2,3t.
Для расчета параметров полиномов необходимо ввести в модель числовые значения для фактора времени t. Это можно сделать двумя способами.
1. Ввести фактор времени линейно, т.е. у первого уровня ряда t1 = 1, у второго t2 = 2, у третьего t3 = 3, у предпоследнего tn–1 = n – 1 и у последнего tn = n.
2. Другой подход заключается в обозначении фактора времени методом условного нуля. Для этого начало координат условно переносится в середину ряда динамики.
Если в ряду нечетное количество уровней, то начало координат 0 совпадает с серединным уровнем ряда. Тогда для серединного уровня ряда ti будет равно 0, а у остальных уровней ti будет указываться со знаками «+» и «-», двигаясь в соответствующие стороны от 0 к крайним уровням ряда динамики.
При четном числе уровней 0 попадает в интервал между серединными уровнями ряда. Строго следуя законам математики, серединным уровням следовало бы присвоить ti = -0,5 и ti = +0,5. Однако, пользуясь свойствами арифметической прогрессии и для упрощения числовых значений ti, серединным уровням присваивают ti = -1 (= -0,5 * 2) и ti = +1 (= 0,5 * 2), а для остальных уровней вводят ti c соответствующим знаком, сохраняя шаг прогрессии 2.
Тогда, если до переноса начала координат ряд ti выглядел как 1, 2, 3, ..., n, то после переноса:
· для нечетного числа уровней ряда ti = …; -3; -2; -1; 0; 1; 2; 3;
· для четного числа уровней ряда ti = …; -5; -3; -1; 1; 3; 5.
Следовательно, ![]() и все
и все ![]() ,
у которых «р» - нечетное число, равны 0. Таким образом, все члены уравнений, содержащие
,
у которых «р» - нечетное число, равны 0. Таким образом, все члены уравнений, содержащие ![]() с такими степенями, могут быть исключены.
Системы нормальных уравнений теперь можно упростить.
с такими степенями, могут быть исключены.
Системы нормальных уравнений теперь можно упростить.
Для прямой при ![]() :
:
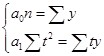
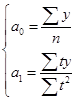 (91)
(91)
Для параболы второго порядка:
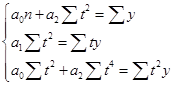 (92)
(92)
Решая системы (91) и (92), получим величины параметров соответствующих полиномов.
Если в ряду динамики цепные абсолютные приросты примерно равны, то аналитическое выравнивание лучше проводить по модели прямой, если при расчете разностей между соседними цепными приростами (вторых разностей) получаются примерно одинаковые значения, то аналитическое выравнивание следует проводить по модели параболы.
Пример 3. Определим основную тенденцию ряда динамики объема оказанных платных услуг населению региона по месяцам 2012 г. (табл. 63).
Исходные и расчетные данные аналитического выравнивания ряда динамики объема оказанных платных услуг населению региона по месяцам 2012 г. (значения фактора времени t заданы методом условного нуля)
|
Месяц |
Объем оказанных платных услуг, млн руб. уi |
ti |
ti2 |
уi*ti (гр. 1 * гр. 2) |
|
|
А |
1 |
2 |
3 |
4 |
5 |
|
январь |
13,3 |
-11 |
121 |
-146,3 |
13,3 |
|
февраль |
13,4 |
-9 |
81 |
-120,6 |
13,4 |
|
март |
13,5 |
-7 |
49 |
-94,5 |
13,5 |
|
апрель |
13,4 |
-5 |
25 |
-67 |
13,6 |
|
май |
13,6 |
-3 |
9 |
-40,8 |
13,7 |
|
июнь |
13,8 |
-1 |
1 |
-13,8 |
13,8 |
|
июль |
14,0 |
1 |
1 |
14 |
13,9 |
|
август |
14,2 |
3 |
9 |
42,6 |
14,0 |
|
сентябрь |
14,1 |
5 |
25 |
70,5 |
14,1 |
|
октябрь |
14,2 |
7 |
49 |
99,4 |
14,2 |
|
ноябрь |
14,3 |
9 |
81 |
128,7 |
14,3 |
|
декабрь |
14,4 |
11 |
121 |
158,4 |
14,4 |
|
Итого |
166,2 |
0 |
572 |
30,6 |
166,2 |
Для каждого уровня
выравниваемого ряда динамики в графе 2 присваиваем обозначение фактора времени t методом условного нуля
таким образом, чтобы ![]() . В качестве
функции выравнивания выбрано уравнение прямой линии:
. В качестве
функции выравнивания выбрано уравнение прямой линии:![]() ,
параметры данного уравнения находим по упрощенным формулам:
,
параметры данного уравнения находим по упрощенным формулам:
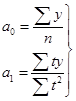
Затем в графах 3 и 4 проводим необходимые расчеты и находим:
![]()
Отсюда:
![]()
![]()
Уравнение прямой будет иметь
вид: ![]() .
.
На основе этого уравнения находятся выровненные месячные уровни (графа 5 таблицы 63) путем подстановки в него соответствующих значений ti (из графы 2).
Параметр а1 полученного уравнения показывает, что объем оказанных платных услуг населению региона в течение 2012 г. возрастал в среднем на 0,0535 млн руб. ежемесячно. Таким образом, величина параметра а1 в уравнении прямой показывает среднюю величину абсолютного прироста выровненного ряда динамики.
Сумма уровней эмпирического ряда
![]() полностью совпала с суммой расчетных
значений выровненного ряда
полностью совпала с суммой расчетных
значений выровненного ряда ![]() .
.
Результаты произведенного
аналитического выравнивания ряда динамики объема оказанных платных услуг
населению региона и исходные данные отражены на рисунке 40. На этом рисунке Ряд 1 – исходные значения, а Ряд 2 – теоретические выровненные
методом аналитического выравнивания значения, рассчитанные по уравнению тренда ![]() .
.
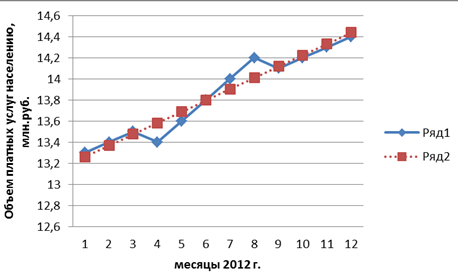
Рис. 40. Динамика объема оказанных платных услуг населению региона по месяцам 2012 г.
Анализ динамики социально-экономических явлений, выявление и характеристика основной тенденции развития дают основание для прогнозирования – определения будущих размеров уровня экономического явления.
Процесс прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, то есть прогноз основан на экстраполяции. Экстраполяция, проводимая в будущее, называется перспективой, а в прошлое – ретроспективой. Обычно, говоря об экстраполяции рядов динамики, подразумевают чаще всего перспективную экстраполяцию.
К простейшим методам экстраполяции относятся: прогнозирование на основе среднего абсолютного прироста, прогнозирование на основе среднего темпа роста и экстраполяция на основе применения метода аналитического выравнивания.
Прогнозирование по среднему абсолютному приросту может быть выполнено в том случае, если есть уверенность считать общую тенденцию линейной, то есть метод основан на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов).
Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения прогнозного значения на k шагов вперед указанными методами необходимо использовать следующие формулы:
Таблица 64.
Формулы расчета прогнозных значений простейшими методами прогнозирования
|
Вид прогнозирования |
Формула расчета |
|
На основе среднего абсолютного прироста |
|
|
На основе среднего темпа роста |
|
|
Обозначения: Уn – фактическое значение конечного уровня ряда;
k – период упреждения (срок) прогноза;
|
|
Пример 4. По данным об объеме оказанных платных услуг населению региона (табл. 63) по месяцам 2012 г. построим помесячный прогноз на I квартал 2013 г. методом среднего абсолютного прироста и методом среднего темпа роста. Для наглядности расчетов представим начальные и конечные уровни, необходимые для расчета среднего абсолютного прироста и среднего темпа роста, в таблице 65.
Таблица 65.
Фрагмент ряда динамики объема оказанных платных услуг населению региона по месяцам 2012 г. (по данным табл.62)
|
Месяцы |
январь |
февраль |
… |
ноябрь |
декабрь |
|
Объем оказанных платных услуг населению, млн.руб. |
13,3 |
13,4 |
… |
14,3 |
14,4 |
Для получения прогнозных значений методом среднего абсолютного прироста:
1) определим средний абсолютный прирост:
![]()
2) по формуле 93 рассчитаем прогнозные значения для следующих трех периодов:
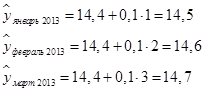
3) определим средний темп роста по формуле:
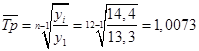
4) используя формулу 94, рассчитаем прогнозные значения для следующих трех периодов:
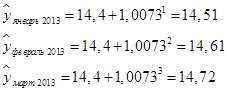
Для удобства сравнения объединим результаты прогнозирования в таблице 66.
Таблица 66.
Прогнозные значения объемов платных услуг населению региона по месяцам I квартала 2013 г. (млн руб.)
|
Месяцы I квартала 2013 г. |
k |
Прогнозные значения, млн руб. |
|
|
методом среднего абсолютного прироста |
методом среднего темпа роста |
||
|
январь |
1 |
14,5 |
14,51 |
|
февраль |
2 |
14,6 |
14,61 |
|
март |
3 |
14,7 |
14,72 |
К недостаткам рассмотренных методов следует отнести то, что они учитывают лишь конечный и начальный уровни ряда, исключая влияние промежуточных уровней. Тем не менее методы среднего абсолютного прироста и среднего темпа роста имеют весьма широкую область применения, что объясняется простотой их вычисления.
Наиболее распространенным методом прогнозирования является расчет прогнозных значений показателя на основе аналитического выражения тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения переменной времени (t). Как правило, для целей прогнозирования расчет параметров уравнения тренда осуществляют, вводя значения фактора времени (t) линейно.
Пример 5. По данным о динамике объема оказанных населению платных услуг по месяцам 2012 г. (млн руб., табл. 67.) построим помесячный прогноз на 1 квартал 2013 г. методом экстраполяции тренда.
Таблица 67.
Таблица исходных и расчетных данных аналитического выравнивания ряда динамики объема оказанных платных услуг населению региона по месяцам 2012 г.
(значения фактора времени t заданы линейно)
|
месяц |
Объем оказанных услуг, млн руб., yi |
ti |
ti2 |
уi * ti |
yt |
|
1 |
13,3 |
1 |
1 |
13,3 |
13,3 |
|
2 |
13,4 |
2 |
4 |
26,8 |
13,4 |
|
3 |
13,5 |
3 |
9 |
40,5 |
13,5 |
|
4 |
13,4 |
4 |
16 |
53,6 |
13,6 |
|
5 |
13,6 |
5 |
25 |
68 |
13,7 |
|
6 |
13,8 |
6 |
36 |
82,8 |
13,8 |
|
7 |
14,0 |
7 |
49 |
98 |
13,9 |
|
8 |
14,2 |
8 |
64 |
113,6 |
14,0 |
|
9 |
14,1 |
9 |
81 |
126,9 |
14,1 |
|
10 |
14,2 |
10 |
100 |
142 |
14,2 |
|
11 |
14,3 |
11 |
121 |
157,3 |
14,3 |
|
12 |
14,4 |
12 |
144 |
172,8 |
14,4 |
|
Итого |
166,2 |
78 |
650 |
1095,6 |
166,2 |
Построим линейную модель тренда
вида: ![]() . Тогда параметры модели определим
через следующую систему уравнений:
. Тогда параметры модели определим
через следующую систему уравнений:
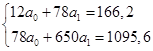
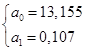
Следовательно, ![]() .
.
Для получения прогнозных значений методом аналитического выравнивания необходимо в полученную модель подставить значения фактора времени t для прогнозируемых месяцев. Продлевая ряд t, узнаем, что для января 2013 г. t = 13, для февраля 2013 г. t = 14, а для марта t = 15. Прогнозные значения представим в табл. 68.
Таблица 68.
Прогнозные значения объема платных услуг населению на I квартал 2013 г. (по месяцам, млн руб.)
|
Месяцы I квартала 2013 г. |
ti |
Прогнозные значения, полученные методом аналитического выравнивания |
|
январь |
13 |
|
|
февраль |
14 |
|
|
март |
15 |
|
1. Что такое ряды динамики? Какие виды рядов динамики вы знаете?
2. Что означает несопоставимость уровней рядов динамики и из-за чего она возникает?
3. Что характеризует: абсолютный прирост, темп роста, темп прироста? В чем разница между этими показателями?
4. Какой показатель является обобщающим показателем абсолютной скорости изменения явления во времени?
5. Что такое тенденция ряда динамики?
6. Для чего применяют метод скользящих средних? В чем основные преимущества и недостатки его использования?
7. В чем состоят исходные предпосылки применения метода аналитического выравнивания?
8. Что такое тренд и уравнение тренда?
9. Какой прием используют для упрощения расчетов параметров уравнения тренда при аналитическом выравнивании ряда динамики?
10. Какие методы экстраполяции вам известны, как они реализуются?
Основная литература:
1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Задание 1.
Имеются следующие данные о размерах страховых выплат страховых организаций РФ за период 2005–2011 гг. (трлн руб.):
|
Годы |
Страховые выплаты, трлн руб. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
2007 |
486,6 |
|
|
|
|
|
|
|
|
2008 |
633,2 |
|
|
|
|
|
|
|
|
2009 |
739,9 |
|
|
|
|
|
|
|
|
2010 |
774,8 |
|
|
|
|
|
|
|
|
2011 |
902,2 |
|
|
|
|
|
|
|
а) Рассчитайте значения индивидуальных аналитических показателей динамики.
б) Рассчитайте значения среднего абсолютного прироста и среднего темпа роста.
в) Рассчитайте прогнозные значения объема страховых выплат на 2012 и 2013 гг. методами среднего абсолютного прироста и среднего темпа роста и занесите их в соответствующие графы сводной таблицы, приведенной ниже:
|
Годы |
k |
Прогнозирование значений объема страховых выплат (трлн руб.) методами: |
|
|
среднего абсолютного прироста |
среднего темпа роста |
||
|
2012 |
|
|
|
|
2013 |
|
|
|
Задание 2.
По данным о динамике среднего размера
вклада (депозита) физических лиц на рублевых счетах в Сбербанке РФ за 2005–2012
гг. (на начало года, тыс. руб.) произведите аналитическое выравнивание ряда и
рассчитайте параметры линейного уравнения тренда. Для обозначения фактора
времени при построении модели используйте метод условного нуля. Рассчитайте
теоретические значения среднего размера вклада![]() используя
полученное уравнение тренда, и занесите их в соответствующую графу таблицы.
используя
полученное уравнение тренда, и занесите их в соответствующую графу таблицы.
|
Годы |
Средний размер вклада, тыс. руб. |
t |
t2 |
y * t |
|
|
2005 |
3,7 |
|
|
|
|
|
2006 |
4,6 |
|
|
|
|
|
2007 |
6,4 |
|
|
|
|
|
2008 |
8,2 |
|
|
|
|
|
2009 |
8,5 |
|
|
|
|
|
2010 |
9,9 |
|
|
|
|
|
2011 |
12,4 |
|
|
|
|
|
2012 |
13,7 |
|
|
|
|
|
Итого: |
|
|
|
|
|
Задание 3.
Вы решили изучить поквартальное количество посетителей своего ресторана, воспользовавшись методом анализа трендов. Линейный тренд описывается уравнением вида уt = 5423 + 408 * t, причем номер квартала начинается с единицы в I квартале 2009 г. и увеличивается на единицу для каждого последующего квартала.
а) Найдите прогнозные значения для четырех кварталов 2013 г.
б) Ваш стратегический бизнес-план развития ресторана включает проект значительного расширения бизнеса (количество посетителей ресторана должно достичь 60 000 за год). В каком году (в соответствии с вашим прогнозом) это должно произойти впервые?
Подсказка: вычислите и сложите четыре прогнозных поквартальных значения, чтобы найти величину показателя за соответствующий год.
Цель изучения темы состоит в формировании системы знаний и компетенций о видах, методах расчета и анализа индексов, оценивающих изменение и развитие социально-экономических явлений и процессов.
В результате успешного освоения темы Вы:
Узнаете:
· что такое экономические индексы и для чего они используются;
· что характеризуют индексы и как они вычисляются;
· какие взаимосвязи существуют между индексами;
· что представляет собой сводный индекс в форме средней;
· как оценить влияние изменений в структуре производства и реализации продукции на ее среднюю себестоимость и цену.
Приобретете компетенции:
· владение методами количественного анализа и моделирования, теоретического и экспериментального исследования;
· способность оценивать воздействие макроэкономической среды на функционирование организаций и органов государственного и муниципального управления;
· умение применять количественные и качественные методы анализа при принятии управленческих решений и строить экономические, финансовые и организационно-управленческие модели;
· способность анализировать финансовую отчетность и принимать обоснованные инвестиционные, кредитные и финансовые решения;
· способность оценивать эффективность использования различных систем учета и распределения затрат, навыки анализа себестоимости продукции и способность принимать обоснованные управленческие решения на основе данных управленческого учета;
· способность обосновывать решения в сфере управления оборотным капиталом и выбора источника финансирования;
· умение рассчитывать индивидуальные и сводные индексы;
· способность оценивать с помощью индексов изменение цен, физического объема, стоимости отдельных товаров и товарных групп;
· умение оценивать изменение себестоимости, выпуска и затрат на выпуск отдельного вида продукции или всего объема производства;
· способность рассчитывать сводные индексы цен и физического объема на основании индивидуальных индексов;
· способность оценивать с помощью индексов влияние структурных изменений в производстве или реализации продукции на ее себестоимость и цену.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:
· индекс;
· динамичный индекс, территориальный индекс;
· индивидуальный индекс, сводный индекс;
· индивидуальный индекс физического объема реализации;
· индивидуальный индекс товарооборота;
· индивидуальный индекс цены;
· индивидуальный индекс себестоимости единицы продукции;
· индивидуальный индекс физического объема производства продукции;
· индивидуальный индекс затрат на производство данного вида продукции;
· сводный индекс товарооборота;
· сводный индекс цен в форме средней геометрической;
· сводный индекс физического объема реализации в форме средней арифметической;
· сводный индекс затрат на производство;
· сводный индекс себестоимости продукции;
· индекс физического объема производства;
· индекс цен переменного состава;
· индекс структурных сдвигов;
· индекс фиксированного состава.
Вопросы темы:
1. Общие понятия об индексах.
2. Индивидуальные индексы.
3. Сводные индексы.
4. Средние формы сводных индексов.
5. Индексный анализ влияния структурных изменений.
Теоретический материал по теме
«Индекс» в переводе с латыни означает «указатель» или «показатель». Индексы служат для сравнения и оценки изменения показателей во времени, в пространстве или по отношению к любому эталону (плану, прогнозу, нормативу).
В статистике индекс – это показатель, который характеризует относительное изменение уровня исследуемого явления в рассматриваемом временном периоде (текущем (отчетном) периоде) по сравнению с другим его уровнем, принятым за базу сравнения (базисным периодом).
В качестве такой базы может быть использован уровень этого явления за какой-либо прошлый период времени (динамический индекс) или уровень того же явления по другой территории (территориальный индекс).
Если оценивают изменение отдельной величины (цены конкретного товара, например автомобиля конкретной марки, или объем выпуска ноутбука определенной модели фирмы Sony) – получают индивидуальный индекс, если анализируется изменение показателя по всей совокупности (по автомобилям всех марок или всем моделям ноутбуков) – получают сводный индекс.
Сводные индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или пространстве две совокупности, элементы которых непосредственно суммировать нельзя. Например, сравнить изменение количества произведенной продукции промышленности за год в абсолютном выражении нельзя, так как оно складывается из объема добычи полезных ископаемых, обрабатывающего производства, объема производства и распределения электроэнергии, объема производства промышленных машин и оборудования и др., несопоставимых по своим свойствам и единицам измерения. Но если выразить объем производства через стоимость, умножив количество произведенной продукции на цену единицы каждого вида, и сопоставить суммарные величины стоимости на конец и на начало года, мы узнаем сводный индекс промышленного производства – значимую и экономически обоснованную сводную индексную величину.
В целом индексный метод направлен на решение следующих задач:
1) характеристика общего изменения уровня сложного социально-экономического явления;
2) анализ влияния каждого фактора, составляющего сложное социально-экономическое явление, на изменение индексируемой величины;
3) анализ влияния структурных сдвигов на изменение индексируемой величины.
В практике индексного метода используются следующие общепринятые обозначения:
i – индивидуальный индекс;
I – сводный индекс;
p – цена;
q – количество;
z – себестоимость единицы продукции;
1 – текущий период;
0 – базисный период.
Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени экономических величин, относящихся к одному объекту:
![]() , (93)
, (93)
где
p1 – цена товара в текущем периоде;
p0 – цена товара в базисном периоде.
Изменение физической массы проданного товара в натуральном выражении измеряется индивидуальным индексом физического объема реализации:
![]() , (94)
, (94)
где
q1 – количество реализованного товара в текущем периоде;
q0 – количество реализованного товара в базисном периоде.
Изменение стоимостного объема товарооборота по данному товару отразится в значении индивидуального индекса товарооборота (индивидуального индекса стоимости). Для его расчета товарооборот текущего периода (произведение цены на количество проданного товара) сравнивается с товарооборотом предшествующего периода:
![]() , (95)
, (95)
где
p1q1 – общая стоимость реализованного товара (товарооборот) в текущем периоде;
p0q0 – общая стоимость реализованного товара (товарооборот) в базисном периоде.
Данный индекс также может быть получен как произведение индивидуального индекса цены и индивидуального индекса физического объема реализации:
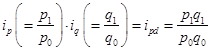
Если рассматривать изменение себестоимости производства отдельного вида продукции, то система индивидуальных индексов будет следующей:
Индивидуальный индекс себестоимости единицы продукции:
![]() , (96)
, (96)
где
z1– себестоимость единицы продукции в текущем периоде;
z0– себестоимость единицы продукции в базисном периоде.
Индивидуальный индекс физического объема производства продукции:
![]() , (97)
, (97)
где
q1 – количество единиц продукции в текущем периоде;
q0 – количество единиц продукции в базисном периоде.
Индивидуальный индекс затрат на производство данного вида продукции:
![]() , (98)
, (98)
где
z1q1 – общие затраты на производство всего объема продукции в текущем периоде;
z0q0 – общие затраты на производство всего объема продукции в базисном периоде.
Взаимосвязь между индексами:
iz * iq = izq
Индивидуальные индексы, в сущности, представляют собой относительные показатели динамики, или темп роста, и по данным за несколько периодов времени могут рассчитываться в цепной или базисной формах.
В отличие от индексов индивидуальных, сводные индексы позволяют обобщить показатели по нескольким позициям (товарам, видам продукции). Исходной формой сводного индекса является агрегатная форма.
Агрегатная форма индекса позволяет найти для разнородной совокупности такой общий показатель, в котором можно объединить все ее элементы. При анализе динамики цен индивидуальные цены различных товаров складывать неправомерно, но суммировать товарооборот по этим товарам вполне допустимо. В текущем периоде такой товарооборот по n товарам составит:
![]()
![]()
Аналогично определяется товарооборот для базисного периода:
![]()
Если мы сравним товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота (сводный индекс стоимости):
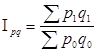 (99)
(99)
Для иллюстрации этого и последующих индексов воспользуемся следующими условными данными (табл. 69):
Цены и объем реализации трех товаров
|
Товар |
Январь |
Февраль |
||
|
цена, руб. |
продано, тыс. шт. |
цена, руб. |
продано, тыс. шт. |
|
|
А |
20 |
9 |
22 |
8 |
|
Б |
60 |
15 |
65 |
13 |
|
В |
30 |
7 |
35 |
11 |
Рассчитаем индекс товарооборота:
![]()
Рассчитанное значение индекса позволяет заключить, что товарооборот в целом по данной товарной группе, состоящей из трех товарных позиций А, Б и В, в текущем периоде по сравнению с базисным возрос на 8,9 % (108,9 – 100,0 %). Отметим, что размер товарной группы (количество товаров) и единицы измерения товаров могут быть любыми.
Величина индекса товарооборота формируется под воздействием двух факторов – на нее оказывает влияние как изменение цен на товары, так и изменение объемов их реализации. Для того чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких показателей, как цена и себестоимость, физический объем реализации обычно фиксируют на уровне текущего периода. Таким способом получают сводный индекс цен (по методу Пааше):
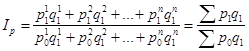 (100)
(100)
Для рассматриваемого примера получим:
![]()
Таким образом, по данной товарной группе цены в феврале по сравнению с январем в среднем возросли на 10,7 %. При построении данного индекса цена выступает в качестве индексируемой величины, а количество проданного товара – в качестве веса.
Рассмотрим сводный индекс цен более подробно. Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, которая показывает, каким бы был товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих двух категорий и отражает имевшее место изменение цен.
Числитель и знаменатель сводного индекса цен также можно интерпретировать и по-другому. Числитель представляет собой сумму денег, фактически уплаченных покупателями за товары в текущем периоде. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились. Разность числителя и знаменателя будет отражать величину экономии (если знак «-») или перерасхода (если «+») покупателей от изменения цен:
![]() (101)
(101)
Необходимо отметить, что на практике также используется сводный индекс цен, построенный по методу Ласпейреса, когда веса или объемы продаж фиксируются на уровне базисного, а не текущего периода:
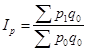
Третьим индексом в рассматриваемой индексной системе (включающим индекс цен, рассчитанный по методу Пааше) является сводный индекс физического объема реализации. Он характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения. Весами в данном случае выступают цены, которые фиксируются на базисном уровне:
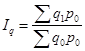 (102)
(102)
В нашем случае индекс составит:
![]()
Физический объем реализации сократился на 1,6 % (98,4 – 100,0 %).
Между рассчитанными индексами существует следующая взаимосвязь:
Ip * Iq = Ipq (103)
Для проверки взаимосвязи переведем значения индексов из процентов в доли единицы и подставим их в формулу 103:
1,107 * 0,984 = 1,089, или 108,9 %, как и по формуле 99
На основе данной взаимосвязи по значениям двух известных индексов всегда можно определить неизвестное значение третьего индекса.
Для оценки изменения уровня производственных издержек рассчитываются сводные индексы затрат (издержек) производства, себестоимости произведенной продукции и физического объема производства.
Сводный индекс затрат на производство оценивает, во сколько раз возросли или уменьшились издержки производства продукции в текущем периоде по сравнению с базисным, или сколько процентов от затрат базисного уровня они составили:
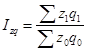 (104)
(104)
Разница между числителем и знаменателем сводного индекса затрат покажет, на сколько рублей увеличились или уменьшились издержки производства в текущем периоде по сравнению с базисным.
Сводный индекс себестоимости продукции показывает, как изменились издержки производства из-за изменения себестоимости в текущем периоде по сравнению с базисным:
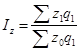 (105)
(105)
Индекс физического объема производства оценивает, во сколько раз изменились издержки производства продукции в результате изменения объема ее производства или сколько процентов составил рост (снижение) издержек из-за изменения физического объема ее производства:
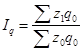 (106)
(106)
Взаимосвязь между индексами выражается формулой:
Iz * Iq = Izq (107)
На практике при расчете индексов часть необходимой информации может отсутствовать или базироваться на результатах выборочных обследований. В подобных случаях вместо индексов в агрегатной форме удобнее использовать средние арифметические и средние гармонические индексы. Любой сводный индекс можно представить как среднюю взвешенную из индивидуальных индексов.
Предположим, мы располагаем данными о стоимости проданной продукции в текущем периоде и индивидуальными индексами цен, полученными, например, в результате выборочного наблюдения. Тогда при расчете сводного индекса цен по методу Пааше можно использовать следующую замену:
![]()
В целом же сводный индекс цен в данном случае будет выражен в форме средней гармонической:
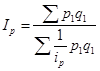 (108)
(108)
Пример. Рассчитаем сводный индекс цен по данным о реализации и ценах трех товаров (табл. 70):
Таблица 70.
Данные о реализации и ценах по товарной группе
|
Товар |
Объем реализации в текущем периоде, руб. |
Изменение цен в текущем периоде по сравнению с базисным, % |
|
А |
44000 |
-1,3 |
|
Б |
56000 |
+4,2 |
|
В |
31000 |
+2,5 |
Последняя графа таблицы содержит информацию об изменениях индивидуальных индексов цен или их приростах. С учетом этих приростов несложно определить первоначальные значения индексов, которые по товарам А, Б и В соответственно составляют 0,987, 1,042 и 1,025.
Рассчитаем значение сводного индекса:
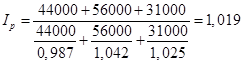
Произведенный расчет позволяет заключить, что цены по данной товарной группе в среднем возросли на 1,9 %. Мы получили значение сводного индекса цен в среднегармонической форме, соответствующее сводному индексу Пааше.
Для получения значения, соответствующего индексу Ласпейреса, сводный индекс цен необходимо представить в среднеарифметической форме. При этом используется следующая замена:
![]()
С учетом этой замены сводный индекс цен в среднеарифметической форме можно представить следующим образом:
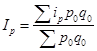 (109)
(109)
Среднеарифметическая форма также может использоваться при расчете сводного индекса физического объема товарооборота. При этом производится замена:
![]()
Сводный индекс физического объема товарооборота в форме средней арифметической имеет вид:
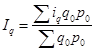 (110)
(110)
Пример. Рассчитаем сводный индекс физического объема реализации продукции по данным о стоимости трех товаров товарной группы (табл. 71):
Таблица 71.
Реализация товаров А, Б, В в натуральном и стоимостном выражении
|
Товар |
Стоимостный объем реализации в базисном периоде, руб. |
Изменение физического объема реализации в текущем периоде по сравнению с базисным, % |
|
А |
87000 |
+3,4 |
|
Б |
54000 |
-12,0 |
|
В |
73000 |
-8,5 |
Индивидуальные индексы физического объема, соответственно, будут равны 1,034, 0,880 и 0,915. С учетом этого рассчитаем среднеарифметический индекс:
![]()
В результате расчета мы получили, что физический объем реализации товаров рассматриваемой товарной группы в среднем снизился на 4,5 %.
Индексы позволяют оценить динамику показателей, характеризующих разнородные в качественном отношении совокупности, как правило, товарные группы. Однако даже если рассматривать данные по каждому товару отдельно или данные о производстве продукции одного вида, на величине результативного показателя будет отражаться влияние структурных изменений, например, изменений в структуре производства или реализации данного товара по территориям. Рассмотрим случай, когда один товар или вид продукции реализуется или производится в нескольких местах (табл. 72).
Таблица 72.
Данные о ценах и объемах реализации товара «X» в регионах
|
Регион |
2011 |
2012 |
||
|
цена, тыс. руб. |
продано, шт. |
цена, тыс. руб. |
продано, шт. |
|
|
1 |
7 |
36000 |
8 |
10000 |
|
2 |
5 |
12000 |
6 |
34000 |
Проведем анализ изменения цен на данный товар. Из таблицы видно, что цена в каждом регионе возросла. Для сводной оценки этого роста воспользуемся средними показателями. Так как в данном случае реализуется один и тот же товар, вполне правомерно рассчитать его среднюю цену за 2011 и за 2012 гг.
Индекс цен переменного состава представляет собой соотношение средних значений за два рассматриваемые периода:
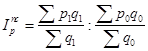 (111)
(111)
![]()
Рассчитанное значение индекса указывает на снижение средней цены данного товара на 0,8 %, т.е. с 6,50 до 6,45 тыс. руб. В то же время из приведенной выше таблицы видно, что цена в каждом регионе в 2012 г. по сравнению с 2011 г. возросла. Данное несоответствие объясняется влиянием изменения структуры реализации товаров по регионам: в 2011 г. по более высокой цене 7 тыс. руб. продали товара втрое больше, чем по цене 5 тыс. руб., а в 2012 г. ситуация принципиально изменилась. Иными словами, на динамике средней цены данного товара отразились структурные сдвиги в рассматриваемой совокупности. Оценить воздействие этого фактора можно с помощью индекса структурных сдвигов:
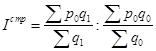 (112)
(112)
![]()
Первая формула в этом индексе позволяет ответить на вопрос, какой была бы средняя цена в 2012 г., если бы цены в каждом регионе сохранились на уровне 2011 г. Вторая часть формулы отражает фактическую среднюю цену 2011 г. В целом по значению индекса мы можем сделать вывод, что за счет структурных сдвигов цены снизились в среднем на 16,1 % (83,9 – 100 = -16,1 %).
Последним в данной системе является индекс цен фиксированного состава, который не учитывает влияние структуры и рассчитывается по уже известной нам формуле сводного индекса цен по методу Пааше:
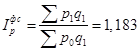
Полученное значение индекса позволяет сделать вывод о том, что если бы структура реализации товара Х по регионам не изменилась, средняя цена возросла бы на 18,3 %. Однако влияние на среднюю цену фактора структурных изменений оказалось сильнее, и в итоге цена даже несколько снизилась. Данное взаимодействие рассматриваемых факторов отражается в следующей взаимосвязи:
![]() (113)
(113)
1,183 * 0,839 = 0,992
Аналогично строятся индексы структурных сдвигов, переменного и фиксированного состава для анализа изменения себестоимости, урожайности и других показателей.
1. Что характеризует экономический индекс?
2. Чем отличается индивидуальный индекс от сводного индекса?
3. В каких единицах измерения выражаются индексы?
4. Что показывает разность между числителем и знаменателем сводного индекса цен? Как интерпретируется ее отрицательное значение?
5. При помощи какого показателя можно оценить снижение издержек производства, вызванное изменением себестоимости единиц выпускаемой продукции?
6. Что представляет собой индекс в форме средней?
7. Можно ли рассчитать сводный индекс переменного состава, зная средние цены реализации товаров за два квартала?
8. Что оценивает индекс структурных сдвигов?
9. Что характеризует индекс фиксированного состава?
Основная литература:
1. Улитина Е.В. Статистика: учебное пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Четыркин Е.М. Финансовая математика. – М.: Дело Лтд, 2006.
5. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Задание 1.
По данным о себестоимости и объемах производства продукции промышленного предприятия определите:
а) сводный индекс себестоимости;
б) сводный индекс физического объема продукции;
в) сводный индекс затрат на производство;
г) покажите взаимосвязь сводных индексов.
|
Изделие |
2011 |
2012 |
Расчетные графы |
||||
|
себесто-имость единицы продукции, руб. |
произ-ведено тыс. шт. |
себесто-имость единицы продукции, руб. |
произ-ведено тыс. шт. |
|
|
|
|
|
А |
220 |
63,4 |
247 |
52,7 |
|
|
|
|
Б |
183 |
41,0 |
215 |
38,8 |
|
|
|
|
В |
67 |
89,2 |
70 |
91,0 |
|
|
|
|
Итого |
|
|
|
|
|
|
|
Задание 2.
Определите общее изменение себестоимости продукции промышленного предприятия в 2012 г. по сравнению с 2011 г. и обусловленный этим изменением размер экономии или дополнительных затрат предприятия по следующим данным.
|
Изделие |
Общие затраты на производство в 2012 г., тыс. руб. |
Изменение себестоимости изделия в 2012 г. по сравнению с 2011 г., % |
Расчетные графы |
|
|
|
|
|||
|
Электромясорубка |
1234 |
+6,0 |
|
|
|
Кухонный комбайн |
5877 |
+8,4 |
|
|
|
Миксер |
980 |
+1,6 |
|
|
|
Итого |
|
|
|
|
Задание 3.
По данным о строительно-производственной деятельности двух ДСК города рассчитайте:
а) индекс себестоимости переменного состава;
б) индекс себестоимости фиксированного составов;
в) индекс структурных сдвигов;
г) проверьте взаимосвязь индексов.
|
Домостроительный комбинат |
Построено жилья, тыс. м2 |
Себестоимость 1 м2, тыс. руб. |
Расчетные графы |
||||
|
2011 |
2012 |
2011 |
2012 |
|
|
|
|
|
ДСК-1 |
53 |
68 |
16,4 |
17,2 |
|
|
|
|
ДСК-2 |
179 |
127 |
16,0 |
16,5 |
|
|
|
|
Итого |
|
|
|
|
|
|
|
ID:0005613