Общая постановка задачи нахождения границы эффективных портфелей
Если портфель состоит из более чем из 2 ценных бумаг, то для любого заданного уровня доходности существует бесконечное число портфелей, или, иными словами, можно сформулировать бесконечное количество портфелей, имеющих одну и ту же доходность.
Тогда задача инвестора сводится к следующему: из всего бесконечного набора портфелей с ожидаемой доходностью E(rn) необходимо найти такой, который обеспечивал бы минимальный уровень риска. Иными словами, можно задачу инвестора свести к следующему:
необходимо найти минимальное значение дисперсии портфеля
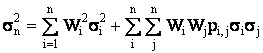 (9)
(9)
при заданных начальных условиях:
E(rпортфеля) =![]() (10)
(10)
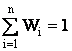 (11)
(11)
Для решения задачи нахождения оптимального портфеля, содержащего n ценных бумаг, необходимо первоначально вычислить:
а) n значений ожидаемой доходности E(ri), где i = 1, 2,…, nкаждой ценной бумаги в портфеле;
б) n значений дисперсий si2 каждой ценной бумаги;
в) n(n-1)/2 значений ковариации si2,j, где i,j = 1, 2,…, n.
Если подставить значения E(ri), si и si,j в выражения (9 – 11), то выясняется, что в этих уравнениях неизвестными оказываются только величины Wi – “веса” каждой ценной бумаги в портфеле. Следовательно, задача формирования оптимального портфеля из n ценных бумаг по сути дела сводится к следующему: для выбранной величины доходности Е* инвестор должен найти такие значения Wi, при которых риск инвестиционного портфеля становится минимальным. Иначе говоря, для выбранного значения Е* инвестор должен определить, какие суммы инвестиционных затрат необходимо направить на приобретение той или иной ценной бумаги, чтобы риск инвестиционного портфеля оказался минимальным.