3.6.2. Основы реляционной алгебры
С точки зрения внешнего представления (абстрагирования на логическом уровне) объектов реального мира модель данных – это основные понятия и способы, используемые при анализе и описании предметной области.
Среди многих попыток представить обработку данных на формальном абстрактном уровне реляционная модель, предложенная Э.Ф. Коддом, стала по существу первой работоспособной моделью данных, поскольку помимо средств описания объектов имела эффективный инструментарий преобразований этих описаний - операции реляционной алгебры.
Реляционная алгебра в том виде, в котором она была определена Э.Ф. Коддом, состоит из двух групп по четыре оператора.
1. Традиционные операции над множествами (но модифицированные с учетом того, что их операндами являются отношения, а не произвольные множества): объединение, пересечение, разность и декартово произведение.
2. Специальные реляционные операции: выборка, проекция, соединение, деление.
Рассмотрим подробнее операции реляционной алгебры.
Объединение возвращает отношение, содержащее все кортежи, которые принадлежат либо одному из двух заданных отношений, либо им обоим.
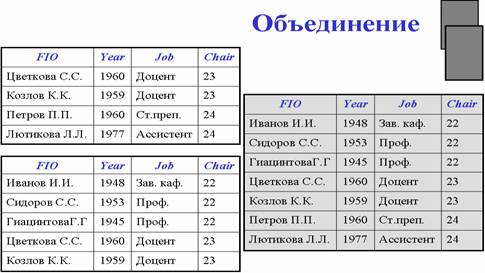
Пересечение возвращает отношение, содержащее все кортежи, которые принадлежат одновременно двум заданным отношениям.
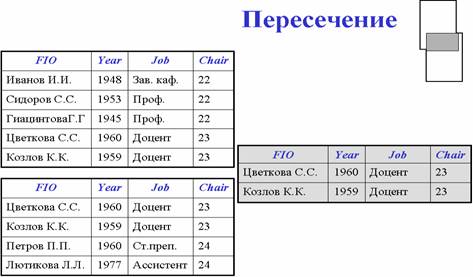
Разность возвращает отношение, содержащее все кортежи, которые принадлежат первому из двух заданных отношений и не принадлежат второму.
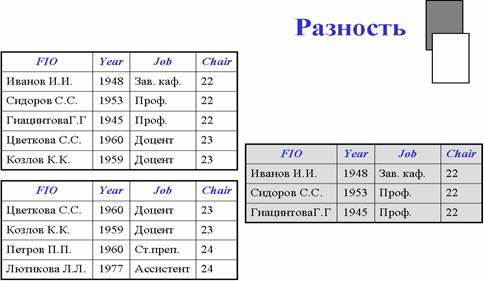
Произведение - возвращает отношение, содержащее все возможные кортежи, которые являются сочетанием двух кортежей, принадлежащих соответственно двум заданным отношениям.
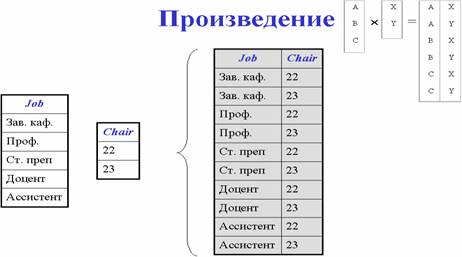
Выборка – возвращает отношение, содержащие все кортежи из заданного отношения, которые удовлетворяют указанным условиям.
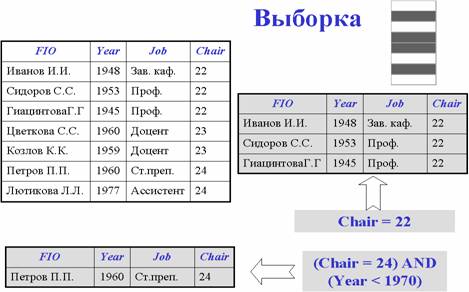
Проекция возвращает отношение, содержащее все кортежи (подкортежи) заданного отношения, которые остались в этом отношении после исключения из него некоторых атрибутов.
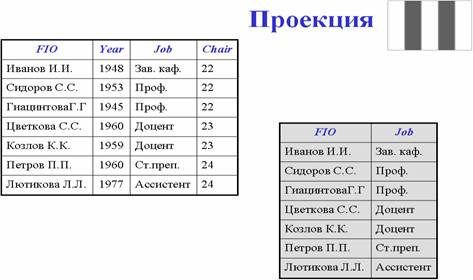
Соединение возвращает отношение, содержащее все возможные кортежи, которые представляют собой комбинацию атрибутов двух кортежей, принадлежащих двум заданным, при условии, что в этих двух комбинированных кортежах присутствуют одинаковые значения в одном или нескольких общих для исходных отношений атрибутах (причем эти общие значения в результирующем кортеже появляются один раз, а не дважды).
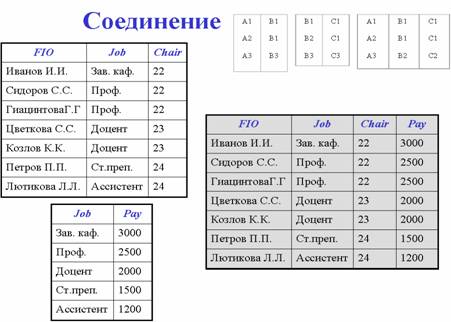
Деление для заданных двух унарных отношений и одного бинарного возвращает отношение, содержащее все кортежи из первого унарного отношения, которые содержатся также в бинарном отношении и соответствуют всем кортежам во втором унарном отношении.
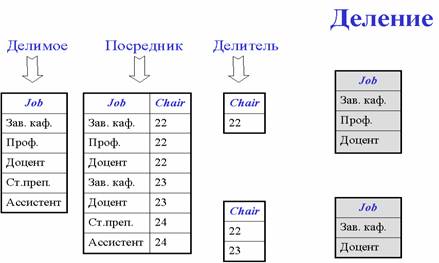
Результат выполнения любой операции над отношением также является отношением, поэтому результат одной операции может использоваться в качестве исходных данных для другой. Другими словами, можно записывать вложенные реляционные выражения, т.е. выражения, в которых операторы сами представлены реляционными выражениями, причем произвольной сложности. Эта особенность называется свойством реляционной замкнутости.
Важно, как отмечается в [4], что отношение имеет две части - заголовок и тело. Нестрого говоря, заголовок - это атрибуты, а тело - это картежи. Заголовок для базового отношения, т.е. значение базовой переменной-отношения, очевидно, вполне конкретен и известен системе, поскольку он задается как часть определения соответствующей базовой переменной-отношения. Т.к. результат обязательно должен иметь вполне определенный тип отношения, поэтому, если рассматривать свойство реляционной замкнутости более строго, каждая реляционная операция должна быть определена таким образом, чтобы выдавать результат с надлежащим типом отношения (в частности, с соответствующим набором имен атрибутов или заголовком).
Реляционная алгебра имеет набор правил вывода типов (отношений), позволяющих вывести тип (отношение) на выходе произвольной реляционной операции, зная типы (отношения) на входе этой операции. Задав такие правила для всех операций, можно гарантировать, что для реляционного выражения любой сложности будет вычисляться результат, имеющий вполне определенный тип (отношение) и, в частности, известный набор имен атрибутов.
Рассмотренные восемь операторов Кодда не являются минимальным набором, так как не все из них примитивны, т.е. часть из них можно определить через другие операторы. Действительно, операции соединения, пересечения и деления можно определить через остальные пять. Эти пять операций (выборка, проекция, произведение, объединение и разность) можно рассматривать как примитивные в том смысле, что ни одна из них не выражается через другие. Они образуют минимальный набор, но, тем не менее, необязательно единственно возможный. Кроме того, остальные три операции (в особенности операция соединения) на практике используются настолько часто, что, несмотря на то, что они не являются примитивными, имеет смысл обеспечить их непосредственную поддержку.
Предшествующее рассмотрение алгебры представлено в контексте только операций выборки данных. Однако, как отмечается в классических введениях к реляционной алгебре, ее основная цель - обеспечить запись реляционных выражений позволяющих определять:
- области выборки, т.е. тех данных, которые должны быть доставлены в результате выполнения операции выборки;
- области обновления, т.е. данных, которые должны быть вставлены, изменены или удалены в результате выполнения операции обновления;
- правила поддержки целостности данных, т.е. некоторых особых требований, которым должна удовлетворять база данных;
- производные переменные-отношения, т.е. те данные, которые должны быть включены в представления базы данных;
- требования устойчивости, т.е. данные, которые должны быть включены в контролируемую область для некоторых операций управления параллельным доступом к информации;
- ограничения защиты, т.е. данные, для которых осуществляется тот или иной тип контроля доступа.
В целом, выражения реляционной алгебры служат для символического высокоуровневого представления намерений пользователя (например, в отношении некоторого определенного запроса). И именно потому, что подобные выражения являются символическими и высокоуровневыми, ими можно манипулировать в соответствии с различными высокоуровневыми правилами преобразования, в том числе и для оптимизации процедур выполнения запросов на данные.
Контрольные вопросы
1. Дайте определение понятия предметной области
2. Что является результатом абстрагированного описания предметной области?
3. Приведите варианты модели трехуровнего представления ПрО.
4. Дайте определение атрибутивного способа идентификации объектов и записей.
5. Приведите типологию простых запросов.
6. Определите понятия первичного и вторичного ключа записи.
7. Определите основные требования к модели данных.
8. Дайте сравнительную характеристику понятий модель данных и модель базы данных.
9. Перечислите операции реляционной алгебры.
10. Дайте определение понятия реляционной замкнутости.
11. Дайте определение реляционных операций соединения, пересечения и деления через пять других операций.
12. Докажите ассоциативность и коммутативность реляционной операции объединения
13. Являются ли реляционные операции умножения и деления взаимообратными?
14. Дайте сравнительную характеристику понятий структура данных, структура записи, структура информации.
15. Дайте определение древовидной структуры.
16. Определите характерные свойства и отличия линейных и нелинейных структур.
17. Проведите сравнительный анализ основных типов нелинейных структур.
18. Перечислите основные свойства реляционной структуры данных.