Целью изучения курса «Методы оптимальных решений» является формирование у студентов теоретических знаний, практических навыков по вопросам, касающимся принятия оптимальных решений в организационно-экономических и производственных системах, с использованием различных методов, т.е. тех инструментов, с помощью которых в современных условиях формируются и анализируются варианты управленческих решений.

Задачи курса «Методы оптимальных решений»:

· обучение теории и практике принятия решений в современных условиях хозяйствования с использованием количественных и качественных методов;

· рассмотрение широкого круга задач, возникающих в практике менеджмента и связанных с принятием решений, относящихся ко всем областям и уровням управления;

· обучение будущих специалистов теории и практике применения количественных и качественных методов для обоснования решений во всех областях целенаправленной деятельности.

В результате изучения дисциплины студент должен:

Иметь представление:

· о путях оптимизации процесса принятия решений с применением количественных и качественных методов;

· об особенностях принятия оптимальных решений в условиях изменения внешней среды.

Знать:

· основные количественные и качественные методы и модели принятия оптимальных решений;

· области применения количественных и качественных методов принятия оптимальных решений;

· содержательную сторону задач, возникающих в практике менеджмента и маркетинга, т.е. уметь идентифицировать проблему.

Уметь:

· пользоваться количественными и качественными методами принятия оптимальных решений, с помощью которых в современных условиях формируются и анализируются варианты управленческих решений:

o уточнять совместно с ЛПР постановку задачи;

o собирать необходимую информацию;

o строить математическую модель задачи;

o интерпретировать полученные результаты и представлять их ЛПР;

o выбирать метод принятия оптимальных решений.

Иметь навык:

· использования количественных и качественных методов при решении специфических задач, возникающих в процессе принятия оптимальных решений;

· применения информационных технологий в процессе моделирования и оптимизации оптимальных решений.

Тема 1. Основы принятия управленческих решений

Цели и задачи:

Цель изучения данной темы – получение общетеоретических знаний о процессе принятия управленческих решений.

Задачи изучения данной темы:

· ознакомление с понятием и сущностью управленческих решений;

· рассмотрение классификации управленческих решений;

· рассмотрение роли человека в процессе принятия управленческих решений.

Вопросы темы:

1. Сущность и характерные особенности управленческих решений.

2. Классификация управленческих решений.

3. Факторы, определяющие качество и эффективность управленческих решений.

4. Люди и их роли в процессе принятия решений.

5. Альтернативы и критерии.

Вопрос 1. Сущность и характерные особенности управленческих решений.

Важнейшим резервом повышения эффективности всего общественного производства является повышение качества решений, принимаемых руководителями.

Понятие «решение» в современной жизни весьма многозначно. Оно понимается и как процесс, и как акт выбора, и как результат выбора. Основная причина неоднозначной трактовки понятия «решение» заключается в том, что каждый раз в это понятие вкладывается смысл, соответствующий конкретному направлению исследований.

Решение как процесс характеризуется тем, что он, протекая во времени, осуществляется в несколько этапов. В связи с этим здесь уместно говорить об этапах подготовки, принятия и реализации решений. Этап принятия решений можно трактовать как акт выбора, осуществляемый индивидуальным или групповым лицом, принимающим решение (ЛПР), с помощью определенных правил.

Решение как результат выбора обычно фиксируется в письменной или устной форме и включает в себя план (программу) действий по достижению поставленной цели.

Решение является одним из видов мыслительной деятельности и проявлением воли человека. Его характеризуют следующие признаки:

· возможность выбора из множества альтернативных вариантов: если нет альтернатив, то нет выбора и, следовательно, нет и решения;

· наличие цели: бесцельный выбор не рассматривается как решение;

· необходимость волевого акта ЛПР при выборе решения, так как ЛПР формирует решение через борьбу мотивов и мнений.

Соответственно, под управленческим решением (УР) понимается:

1) поиск и нахождение наиболее эффективного, наиболее рационального или оптимального варианта действий руководителя;

2) конечный результат постановки и выработки УР.

Наибольший интерес представляет процесс принятия и реализации решений как последовательная смена взаимоувязанных стадий, этапов различных действий руководителя, вскрывающая технологию мыслительных действий, поисков истины и анализа заблуждений, путей движения к цели и средств ее достижения. Только такой подход позволяет понять зафиксированный акт управленческого решения, источники его происхождения.

К управленческому решению предъявляется ряд требований, к числу которых можно отнести:

1) всестороннюю обоснованность решения;

2) своевременность;

3) необходимую полноту содержания;

4) полномочность;

5) согласованность с принятыми ранее решениями.

Всесторонняя обоснованность решения означает, прежде всего, необходимость принятия его на базе максимально полной и достоверной информации. Однако только этого недостаточно. Решение должно охватывать весь спектр вопросов, всю полноту потребностей управляемой системы. Для этого необходимо знание особенностей, путей развития управляемой, управляющей систем и окружающей среды. Требуется тщательный анализ ресурсного обеспечения, научно-технических возможностей, целевых функций развития, экономических и социальных перспектив предприятия, региона, отрасли, национальной и мировой экономики. Всесторонняя обоснованность решений требует поиска новых форм и путей обработки научно-технической и социально-экономической информации, то есть формирования передового профессионального мышления, развития его аналитико-синтетических функций.

Своевременность управленческого решения означает, что принятое решение не должно ни отставать, ни опережать потребности и задачи социально-экономической системы. Преждевременно принятое решение не находит подготовленной почвы для его реализации и развития и может дать импульсы для развития негативных тенденций. Запоздалые решения не менее вредны для общества. Они не способствуют решению уже «перезревших» задач и еще более усугубляют и без того болезненные процессы.

Необходимая полнота содержания решений означает, что решение должно охватывать весь управляемый объект, все сферы его деятельности, все направления развития. В наиболее общей форме управленческое решение должно охватывать:

a) цель (совокупность целей) функционирования и развития системы;

b) средства и ресурсы, используемые для достижения этих целей;

c) основные пути и способы достижения целей;

d) сроки достижения целей;

e) порядок взаимодействия между подразделениями и исполнителями;

f) организацию выполнения работ на всех этапах реализации решения.

Важным требованием управленческого решения является полномочность (властность) решения – строгое соблюдение субъектом управления тех прав и полномочий, которые ему предоставлены высшим уровнем управления. Сбалансированность прав и ответственности каждого органа, каждого звена и каждого уровня управления – постоянная проблема, связанная с неизбежным возникновением новых задач развития и отставанием от них системы регламентации и регулирования.

Согласованность с принятыми ранее решениями означает также необходимость соблюдения четкой причинно-следственной связи общественного развития. Она необходима для соблюдения традиций уважения к закону, постановлениям, распоряжениям. На уровне отдельной фирмы она необходима для осуществления последовательной научно-технической, рыночной и социальной политики, четкого функционирования производственного аппарата.

Согласованность с принятыми ранее решениями означают также необходимость соблюдения четкой причинно-следственной связи общественного развития. Если необходимо, должны отменяться принятые ранее решения, вступившие в противоречия с новыми условиями существования системы. Появление противоречащих друг другу решений есть прежде всего следствие плохого познания и понимания законов общественного развития, проявления низкого уровня управленческой культуры.

Принятие УР требует высокого уровня профессионализма и наличия определенных социально-психологических качеств личности, чем обладают не все специалисты, имеющие профессиональное образование, а всего лишь 5–10 % из них.

Основными факторами, оказывающими влияние на качество управленческого решения, являются: применение к системе менеджмента научных подходов и принципов, методов моделирования, автоматизация управления, мотивация качественного решения и др.

Обычно в принятии любого решения присутствуют в различной степени три момента – интуиция, суждение и рациональность.

При принятии чисто интуитивного решения люди основываются на собственном ощущении того, что их выбор правилен. Здесь присутствует «шестое чувство», своего рода озарение, посещаемое, как правило, представителей высшего эшелона власти. Менеджеры среднего звена больше полагаются на получаемую информацию и помощь ЭВМ. Несмотря на то, что интуиция обостряется вместе с приобретением опыта, продолжением которого как раз и является высокая должность, менеджер, ориентирующийся только на нее, становится заложником случайности, и с точки зрения статистики шансы его на правильный выбор не очень высоки.

Решения, основанные на суждении, во многом сходны с интуитивными, вероятно потому, что, на первый взгляд, их логика слабо просматривается. Но все же в их основе лежат знания и осмысленный, в отличие от предыдущего случая, опыт прошлого. Используя их и опираясь на здравый смысл, с поправкой на сегодняшний день, выбирается тот вариант, который принес наибольший успех в аналогичной ситуации в прежнее время. Однако здравый смысл у людей встречается редко, поэтому данный способ принятия решений тоже не очень надежен, хотя подкупает своей быстротой и дешевизной.

Другая слабость в том, что суждение невозможно соотнести с ситуацией, которая прежде не имела места, и поэтому опыта ее решения просто нет. Кроме того, руководитель при таком подходе стремится действовать преимущественно в тех направлениях, которые ему хорошо знакомы, в результате чего рискует упустить хороший результат в другой области, сознательно или бессознательно отказываясь от вторжения в нее.

Мощным фактором, активизирующим процесс принятия решения, выступают современные средства оргтехники, включая вычислительные сети. Это требует высокого уровня культуры в области математики и программирования, технологии использования технических средств. Однако процесс принятия решения, выбора конкретного варианта всегда будет иметь творческий характер и зависеть от конкретной личности.

Вопрос 2. Классификация управленческих решений.

Классификация УР необходима для определения общих и конкретно-специфических подходов к их разработке, реализации и оценке, что позволяет повысить их качество, эффективность и преемственность. УР могут быть классифицированы самыми разнообразными способами. Наиболее распространенными являются следующие принципы классификации:

1) по функциональному содержанию;

2) по характеру решаемых задач (сфере действия);

3) по иерархии управления;

4) по характеру организации разработки;

5) по характеру целей;

6) по причинам возникновения;

7) по исходным методам разработки;

8) по организационному оформлению.

УР могут быть классифицированы по функциональному содержанию, т.е. по отношению к общим функциям управления, например:

a) плановые решения;

b) организационные решения;

c) контролирующие решения;

d) прогнозирующие решения.

Обычно такие решения затрагивают в той или иной мере все функции управления, однако в каждом из них можно выделить основное ядро, связанное с какой-то основной функцией.

Другой принцип классификации связан с характером решаемых задач:

a) экономических;

b) организационных;

c) технологических;

d) технических;

e) экологических и прочих.

Чаще всего УР связаны не с одной, а с рядом задач, в той или иной степени имея комплексный характер.

По уровням иерархии систем управления выделяют УР: на уровне больших систем (БС); на уровне подсистем; на уровне отдельных элементов системы. Обычно инициируются общесистемные решения, которые затем доводятся до элементарного уровня, однако возможен и обратный вариант.

В зависимости от организации разработки решений выделяются следующие УР:

a) единоличные;

b) коллегиальные;

c) коллективные.

Предпочтение способа организации выработки УР зависит от многих причин: компетентности руководителя, уровня квалификации коллектива, характера задач, ресурсов и т.д.

По характеру целей принимаемые решения могут быть представлены как:

a) текущие (оперативные);

b) тактические;

c) стратегические.

По причинам возникновения УР делятся на:

a) ситуационные, связанные с характером возникающих обстоятельств;

b) принимаемые по предписанию (распоряжению) вышестоящих органов;

c) программные, связанные с включением данного объекта управления в определенную структуру программно-целевых отношений, мероприятий;

d) инициативные, связанные с проявлением инициативы системы, например в сфере производства товаров, услуг, посреднической деятельности;

e) эпизодические и периодические, вытекающие из периодичности воспроизводственных процессов в системе (например, сезонности сельскохозяйственного производства, сплава леса по рекам, геологических работ).

Важным классификационным подходом служат исходные методы разработки УР. К их числу можно отнести:

a) графические методы, с использованием графоаналитических подходов (сетевых моделей и методов, ленточных графиков, структурных схем, декомпозиции больших систем);

b) математические методы, предполагающие формализацию представлений, отношений, пропорций, сроков, событий, ресурсов;

c) эвристические методы, связанные с широким использованием экспертных оценок, разработки сценариев, ситуационных моделей.

По организационному оформлению УР делятся на:

a) жесткие, однозначно задающие дальнейший путь их воплощения;

b) ориентирующие, определяющие направление развития системы;

c) гибкие, изменяющиеся в соответствии с условиями функционирования и развития системы;

d) нормативные, задающие параметры протекания процессов в системе.

Поскольку решения принимаются людьми, то их характер во многом несет на себе отпечаток личности менеджера, причастного к их появлению на свет. В связи с этим принято различать уравновешенные, импульсивные, инертные, рискованные и осторожные решения.

Уравновешенные решения принимают менеджеры, внимательно и критически относящиеся к своим действиям, выдвигаемым гипотезам и их проверке. Обычно, прежде чем приступить к принятию решения, они имеют сформулированную исходную идею.

Авторы импульсивных решений легко генерируют самые разнообразные идеи в неограниченном количестве, но не в состоянии их как следует проверить, уточнить, оценить. Решения поэтому оказываются недостаточно обоснованными и надежными, принимаются «с наскока», «рывками».

Инертные решения становятся результатом осторожного поиска. В них, наоборот, контрольные и уточняющие действия преобладают над генерированием идей, поэтому в таких решениях трудно обнаружить оригинальность, блеск, новаторство.

Рискованные решения отличаются от импульсивных тем, что их авторы не нуждаются в тщательном обосновании своих гипотез и, если уверены в себе, могут не испугаться любых опасностей.

Осторожные решения характеризуются тщательностью оценки менеджером всех вариантов, сверхкритичным подходом к делу. Они в еще меньшей степени, чем инертные, отличаются новизной и оригинальностью.

Перечисленные виды решений принимаются в основном в процессе оперативного управления персоналом. Для стратегического и тактического управления любой подсистемы системы менеджмента принимаются рациональные решения, основанные на методах экономического анализа, обоснования и оптимизации.

Вопрос 3. Факторы, определяющие качество и эффективность управленческих решений.

Под качеством управленческих решений следует понимать степень соответствия УР характеру разрешаемых задач функционирования и развития производственных систем – иначе говоря, в какой степени УР обеспечивает дальнейшие пути развития производственной системы в условиях формирования рыночных отношений.

Факторы, определяющие качество и эффективность управленческих решений, могут классифицироваться по различным признакам – как факторы внутренней природы (связанные с управляющей и управляемой системами), так и внешние факторы (влияние окружающей среды). К числу этих факторов следует отнести:

1) законы объективного мира, связанные с принятием и реализацией УР;

2) четкую формулировку цели – для чего принимается УР, какие реальные результаты могут быть достигнуты, как измерить, соотнести поставленную цель и достигнутые результаты;

3) объем и ценность располагаемой информации – для успешного принятия УР главным является не объем информации, а ценность, определяемая уровнем профессионализма, опыта, интуицией кадров;

4) время разработки УР – как правило, управленческое решение всегда принимается в условиях дефицита времени и чрезвычайных обстоятельств (дефицита ресурсов, активности конкурентов, рыночной конъюнктуры, непоследовательного поведения политиков);

5) организационные структуры управления;

6) формы и методы осуществления управленческой деятельности;

7) методы и методики разработки и реализации УР (например, если фирма лидирует – методика одна, если следует за другими – иная);

8) субъективность оценки варианта выбора решения. Чем более неординарным является УР, тем субъективнее оценка;

9) состояние управляющей и управляемой систем (психологический климат, авторитет руководителя, профессионально-квалификационный состав кадров и т.д.);

10) систему экспертных оценок уровня качества и эффективности УР.

Управленческие решения должны опираться на объективные законы и закономерности общественного развития. С другой стороны, УР существенным образом зависят от множества субъективных факторов – логики разработки решений, качества оценки ситуации, структуризации задач и проблем, определенного уровня культуры управления, механизма реализации решений, исполнительской дисциплины и т.п. При этом необходимо всегда помнить, что даже тщательно продуманные решения могут оказаться неэффективными, если они не смогут предвосхитить возможных изменений в ситуации, в состоянии производственной системы.

Вопрос 4. Люди и их роли в процессе принятия решений.

В процессе принятия решений люди могут играть разные роли. Будем называть человека, фактически осуществляющего выбор наилучшего варианта действий, лицом, принимающим решения (ЛПР). Наряду с ЛПР следует выделить как отдельную роль владельца проблемы – человека, который, по мнению окружающих, должен ее решать и несет ответственность за принятые решения. Но это далеко не всегда означает, что владелец проблемы является также и ЛПР. Конечно, он может быть таковым, и история дает нам многочисленные примеры совмещения этих двух ролей. Но бывают ситуации, когда владелец проблемы является лишь одним из нескольких человек, принимающих участие в ее решении. Он может быть председателем коллективного органа, принимающего решения, вынужденным идти на компромиссы, чтобы достичь согласия. Иногда личности ЛПР и владельца проблемы просто не совпадают. Мы все знаем семьи, в которых номинальный глава семьи ничего не решает. Точно таким же образом некоторые руководители стремятся переложить на других принятие решений: глава фирмы полагается на своего заместителя, а президенты подписывают подготовленные другими (и иногда противоречивые) распоряжения. Таким образом, владелец проблемы и ЛПР могут быть как одной, так и разными личностями.

Третьей ролью, которую может играть человек в процессе принятия решений, является роль руководителя или участника активной группы – группы людей, имеющих общие интересы и старающихся оказать влияние на процесс выбора и его результат. Так, пытаясь повлиять на экономическую политику страны, одни активные группы организуют забастовки, другие – шумную кампанию поддержки правительства в печати, третьи выделяют средства для поддержки правительства – дают займы. Человек осуществляет ответственный выбор, находясь в положении избирателя, который должен решить, за какую личность или за какую политическую партию голосовать. При этом избиратель является одним из многих участников процесса принятия коллективного решения. Если решения принимаются малой группой, члены которой формально имеют равные права (жюри, комиссия), то человек является членом группы, принимающей решения. Главное в деятельности такой группы – достижение согласия при выработке совместных решений.

В процессе принятия решений человек может выступать в качестве эксперта, т.е. профессионала в той или иной области, к которому обращаются за оценками и рекомендациями все люди, включенные в этот процесс. Так, при перестройке организации ЛПР обращается за советом к опытному администратору. Эксперты могут помочь бизнесмену в оценке экономической эффективности выпуска новой продукции и т.д.

При принятии сложных (обычно стратегических) решений в их подготовке иногда принимает участие консультант по принятию решений. Его роль сводится к разумной организации процесса принятия решений – помощи ЛПР и владельцу проблемы в правильной постановке задачи, выявлении позиций активных групп, организации работы с экспертами. Консультант (или аналитик) обычно не вносит свои предпочтения, оценки в принятие решений, он только помогает другим взвесить все «за» и «против» и выработать разумный компромисс.

Кроме того, в принятии решений неявно участвует окружение ЛПР – сотрудники той организации, от имени которой ЛПР принимает решения. Обычно эта группа людей имеет общие взгляды, общие ценностные установки. Именно этой группе ЛПР в первую очередь объясняет логичность, разумность, обоснованность своего решения. В связи с этим, хотя ЛПР принимает индивидуальные решения, оно учитывает политику и предпочтения данной группы лиц.

Вопрос 5. Альтернативы и критерии.

Варианты действий принято называть альтернативами. Альтернативы – неотъемлемая часть проблемы принятия решений: если не из чего выбирать, то нет и выбора. Следовательно, для постановки задачи принятия решений необходимо иметь хотя бы две альтернативы.

Альтернативы бывают независимыми и зависимыми. Независимыми являются те альтернативы, любые действия с которыми (удаление из рассмотрения, выделение в качестве единственно лучшей) не влияют на качество других альтернатив. При зависимых альтернативах оценки одних из них оказывают влияние на качество других. Имеются различные типы зависимости альтернатив. Наиболее простым и очевидным является непосредственная групповая зависимость: если решено рассматривать хотя бы одну альтернативу из группы, то надо рассматривать и всю группу. Так, при планировании развития города решение о сохранении исторического центра влечет за собой рассмотрение всех вариантов его реализации.

Задачи принятия решений существенно различаются также в зависимости от наличия альтернатив на момент выработки политики и принятия решений. Встречаются задачи, когда все альтернативы уже заданы, уже определены, и необходимо лишь выбрать лучшие из этого множества. Например, мы можем искать наиболее эффективную фирму из уже имеющихся, определять лучший университет, лучшую из построенных яхт и т.д.

Особенностью этих задач является замкнутое, нерасширяющееся множество альтернатив. Но существует множество задач другого типа, где все альтернативы или их значительная часть появляются после принятия основных решений. Например, необходимо разработать правило открытия кредитов в банке для организаций или частных лиц. Здесь альтернативы (конкретные организации или лица) принципиально появляются лишь после выработки и оглашения правил.

Когда альтернатив много (сотни и тысячи), внимание ЛПР не может сосредоточиться на каждой из них. В таких ситуациях возрастает необходимость в четких правилах выбора, в процедурах использования экспертов, в разработке совокупности правил, позволяющих проводить в жизнь непротиворечивую и последовательную политику. Во всем этом существует потребность и тогда, когда число альтернатив невелико (до 20). В таких задачах, как, например, выбор плана политической кампании, выбор трассы газопровода, выбор плана развития города, основных альтернатив, с рассмотрения которых начинается выбор, сравнительно немного. Но они не являются единственно возможными. Часто на их основе в процессе выбора возникают новые альтернативы. Первичные, основные альтернативы не всегда удовлетворяют участников процесса выбора. Однако они помогают им понять, чего конкретно не хватает, что реализуемо при данной ситуации, а что нет. Этот класс задач можно назвать задачами с конструируемыми альтернативами.

Критерии.

В современной науке о принятии решений считается, что варианты решений характеризуются различными показателями их привлекательности для ЛПР. Эти показатели называют признаками, факторами, атрибутами или критериями. Мы принимаем для последуюшего изложения термин «критерий».

Мы будем называть критериями оценки альтернатив показатели их привлекательности (или непривлекательности) для участников процесса выбора. В профессиональной деятельности выбор критериев часто определяется многолетней практикой, опытом. В подавляющем большинстве задач выбора имеется достаточно много критериев оценки вариантов решений. Эти критерии могут быть независимыми или зависимыми. Зависимыми называются те критерии, при которых оценка альтернативы по одному из них определяет (однозначно либо с большой степенью вероятности) оценку по другому критерию. Так, мы можем ожидать, что высококачественная элитная квартира является, как правило, дорогой. Зависимость между критериями приводит к появлению целостных образов альтернатив, которые имеют для каждого из участников процесса выбора определенное смысловое содержание. На сложность задач принятия решений влияет также количество критериев. При небольшом числе критериев (два-три) задача сравнения двух альтернатив достаточно проста и прозрачна, качества по критериям могут быть непосредственно сопоставлены и выработан компромисс. При большом числе критериев задача становится малообозримой. К счастью, при большом количестве критериев они обычно могут быть объединены в группы, имеющие конкретное смысловое значение и название. Основанием для естественной группировки критериев является возможность выделить плюсы и минусы альтернатив, их достоинства и недостатки (например, стоимость и эффективность). Такие группы, как правило, независимы. Выявление структуры на множестве критериев делает процесс принятия решений значительно более осмысленным и эффективным.

Оценки по критериям.

Использование критериев для оценки альтернатив требует определения градаций качества – лучших, худших и промежуточных оценок. Иначе говоря, существуют шкалы оценок по критериям.

В принятии решений принято различать шкалы непрерывных и дискретных оценок, шкалы количественных и качественных оценок. Так, для критерия «стоимость» может быть использована непрерывная количественная шкала оценок (в денежных единицах). Для критерия «наличие дачи» может быть качественная двоичная шкала: есть либо нет. Кроме категорий «качественные – количественные», «непрерывные – дискретные» в принятии решений различают следующие типы шкал.

1. Шкала порядка – оценки упорядочены по возрастанию или убыванию качества. Примером может служить шкала экологической чистоты района около места жительства:

· очень чистый район;

· вполне удовлетворительный по чистоте;

· экологическое загрязнение велико.

2. Шкала равных интервалов – интервальная шкала. Для этой шкалы имеются равные расстояния по изменению качества между оценками. Например, шкала дополнительной прибыли для предпринимателя может быть следующей: 1 млн., 2 млн., 3 млн. и т.д. Для интервальной шкалы характерно, что начало отсчета выбирается произвольно, так же как и шаг (расстояние между оценками) шкалы.

3. Шкала пропорциональных оценок – идеальная шкала.

Примером является шкала оценок по критерию стоимости, отсчет в которой начинается с установленного значения (например, с нулевой стоимости).

В принятии решений чаще всего используются порядковые шкалы и шкалы пропорциональных оценок.

Вопросы для самопроверки:

1. Охарактеризуйте шкалу равных интервалов, ее особенности, и приведите финансово-экономический пример использования данной шкалы.

2. Дайте характеристику шкалы порядка.

3. Дайте характеристику шкалы равных интервалов и пропорциональной шкалы.

4. Чем характеризуется зависимость критериев или альтернатив?

Литература по теме:

Основная литература:

1. Литвак Б.Г. Управленческие решения: Практикум. – М.: МФПУ «Синергия», 2012. – 448 с. – (Академия бизнеса).

2. Литвак Б.Г. Управленческие решения: Учебник. – М.: МФПУ «Синергия», 2012. – 512 с. – (Академия бизнеса).

Дополнительная литература:

1. Ларичев О.И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах: Учебник. – М.: Логос, 2008. – 392 с.

2. Смирнов Э.А. Разработка управленческих решений. – М.: ИНФРА-М, 2008. – 272 с.

3. Фатхутдинов Р.А. Разработка управленческого решения: Учеб. пособие. – М.: Бизнес-школа, Интел-Синтез, 2007. – 272 с.

Практические задания:

Дайте определения следующих ключевых понятий:

· принятие решений;

· ЛПР;

· роли людей в процессах принятия решений;

· активные группы;

· индивидуальный выбор;

· альтернативы;

· критерии;

· шкалы критериев;

· процесс принятия решений, его этапы;

· доминирующие и доминируемые альтернативы.

Тема 2. Задачи и методы принятия управленческих решений

Цели и задачи:

Цель изучения данной темы – получение общетеоретических знаний о задачах и методах принятия управленческих решений.

Задачи изучения данной темы:

· формулировка задач принятия решений;

· рассмотрение классификации задач принятия управленческих решений;

· рассмотрение классификации методов принятия управленческих решений;

· изучение предпосылок появления систем поддержки принятия решений.

Вопросы темы:

1. Типовые задачи принятия решений.

2. Классификация задач принятия решений.

3. Классификация методов принятия управленческих решений.

4. Предпосылки появления систем поддержки принятия решений (СППР).

Вопрос 1. Типовые задачи принятия решений.

Из трех приведенных выше этапов процесса принятия решений наибольшее внимание традиционно уделяется третьему этапу. За признанием важности поиска информации и выделения альтернатив следует понимание того, что эти этапы в высшей степени неформализованы. Способы прохождения этапов зависят не только от содержания задачи принятия решений, но и от опыта, привычек, личного стиля ЛПР и его окружения. Хотя эти же факторы присутствуют при сравнении альтернатив, здесь их роль заметно меньше. Научный анализ проблем принятия решений начинается с момента, когда хотя бы часть альтернатив и/или критериев известна.

В современной науке о принятии решений центральное место занимают многокритериальные задачи выбора. Считается, что учет многих критериев приближает постановку задачи к реальной жизни. Традиционно принято различать три основные задачи принятия решений:

1. Упорядочение альтернатив. Для ряда задач представляется вполне обоснованным требование определить порядок на множестве альтернатив. Так, члены семьи упорядочивают по степени необходимости будущие покупки, руководители фирм упорядочивают по прибыльности объекты капиталовложений и т.д. В общем случае требование упорядочения альтернатив означает определение относительной ценности каждой из альтернатив.

2. Распределение альтернатив по классам решений. Такие задачи часто встречаются в повседневной жизни. Так, при покупке квартиры или дома, при обмене квартиры люди обычно делят альтернативы на две группы: заслуживающие и не заслуживающие более подробного изучения, требующего затрат сил и средств. Группы товаров различаются по качеству. Абитуриент делит на группы вузы, в которые он стремится поступить. Точно так же люди часто выделяют для себя группы книг (по привлекательности для чтения), туристские маршруты и т.д.

3. Выделение лучшей альтернативы. Эта задача традиционно считалась одной из основных в принятии решений. Она часто встречается на практике. Выбор одного предмета при покупке, выбор места работы, выбор проекта сложного технического устройства – эти примеры хорошо знакомы. Кроме того, такие задачи распространены в мире политических решений, где альтернатив сравнительно немного, но они достаточно сложны для изучения и сравнения. Например, необходим лучший вариант организации обмена денег, лучший вариант проведения земельной реформы и т.д. Заметим, что особенностью многих задач принятия политических решений является конструирование новых альтернатив в процессе решения проблем.

Вопрос 2. Классификация задач принятия решений.

В настоящее время не существует общепринятой универсальной классификационной схемы задач принятия решений (ЗПР). Можно выделить отдельные важные классификационные признаки, а именно:

1. Количество целей операции, преследуемых одной оперирующей стороной, и соответствующих целям критериев оптимальности.

2. Наличие или отсутствие зависимости критерия оптимальности и дисциплинирующих условий от времени.

3. Наличие случайных и неопределенных факторов, влияющих на исход операции. Этот признак назван признаком «определенность – риск – неопределенность».

По первому классификационному признаку ЗПР делятся на два больших класса – одноцелевые, или однокритериальные (скалярные), и многоцелевые, или многокритериальные (векторные).

По второму классификационному признаку задачи принятия решений делятся на два больших класса – статические и динамические ЗПР. В статических ЗПР критериальная функция и функции ограничений не зависят от времени. Динамические задачи сложнее статических. Динамические задачи отличают две характерные особенности:

1) В качестве критерия оптимальности в динамических ЗПР выступает обычно не функция, как в статических ЗПР, а функционал, зависящий от функций времени, описывающих поведение некоторых динамических объектов, участвующих в операции.

2) В составе дисциплинирующих условий в динамических ЗПР обычно присутствуют так называемые дифференциальные связи. Они представляют собой дифференциальные уравнения, описывающие поведение динамических объектов, участвующих в операции, в качестве примера динамической ЗПР можно привести задачу вывода космического летательного аппарата в заданную точку пространства с заданной точностью и за заданное время с минимальным расходом топлива. В настоящее время динамические ЗПР еще не получили широкого применения в экономических исследованиях. По третьему классификационному признаку «определенность – риск – неопределенность» – ЗПР делятся на три больших класса:

а) Принятие решений при определенности, или, иначе, детерминированные ЗПР. Они характеризуются однозначной, детерминированной связью между принятым решением и его исходом. Это наиболее простой и наиболее изученный случай принятия решений, когда относительно каждой стратегии оперирующей стороны заранее, до проведения операции, известно, что она неизменно приводит к некоторому конкретному результату. В детерминированных ЗПР критерий оптимальности и дисциплинирующие условия зависят только от стратегий оперирующей стороны и фиксированных детерминированных неконтролируемых факторов, т.е. факторов, полностью известных оперирующей стороне.

б) Принятие решений при риске, или, иначе, стохастические ЗПР. В этом случае каждая стратегия оперирующей стороны может привести к одному из множества возможных исходов, причем каждый исход имеет определенную вероятность появления. Предполагается, что принимающему решение эти вероятности заранее, до проведения операции, полностью известны (во всяком случае, могут быть определены с любой требуемой для целей исследования степенью точности). В стохастических ЗПР критерий оптимальности зависит кроме стратегий оперирующей стороны и детерминированных факторов также от фиксированных стохастических факторов, т.е. от случайных факторов, законы распределения которых известны оперирующей стороне. Статистические характеристики (законы распределения, математические ожидания, дисперсии и т.п.) стохастических факторов, а также значения детерминированных факторов являются той исходной информацией, которая может быть использована исследователем операции при определении оптимальной стратегии.

Первое из приведенных названий рассматриваемого класса ЗПР – «принятие решений при риске» – связано со следующими обстоятельствами. Несмотря на то, что все случайные явления и процессы, сопровождающие операцию и влияющие на ее исход, хорошо изучены и все их необходимые статистические характеристики полностью известны, исход каждой конкретной реализации операции заранее (до ее проведения) не известен, случаен. В этом смысле оперирующая сторона всегда рискует (в большей или меньшей степени) получить не тот результат, на который она ориентируется, выбирая свою оптимальную стратегию в расчете на осредненные, статистические характеристики случайных факторов.

в) Принятие решений в условиях неопределенности. В данных ЗПР критерий оптимальности зависит, кроме стратегий оперирующей стороны и фиксированных факторов, также от неопределенных факторов, не подвластных оперирующей стороне и не известных ей в момент принятия решения (или известных с недостаточной для принятия решения точностью). В результате влияния неопределенных факторов каждая стратегия оперирующей стороны оказывается связанной с множеством возможных исходов, вероятности которых либо не известны оперирующей стороне (или известны с недостаточной для принятия решения точностью), либо вовсе не имеют смысла. Первое соответствует неопределенным факторам стохастической природы (т.е. недостаточно изученным стохастическим факторам, относительно которых отсутствует необходимая статистическая информация), второе – неопределенным факторам нестохастической природы.

Детерминированные ЗПР и ЗПР в условиях неопределенности можно считать предельными случаями ЗПР (т.е. полное знание и полное незнание). ЗПР, в которых имеется элемент риска, занимают некоторое промежуточное положение. Очевидно, что любой предельный случай всегда представляет собой большую или меньшую идеализацию реальной ситуации.

Классификацию ЗПР завершим указанием на математический аппарат, применяемый при решении ЗПР того или другого класса. Однокритериальные статические детерминированные ЗПР в своей общей постановке полностью совпадают с общей постановкой задачи математического программирования (МП), представляющего собой бурно развивающуюся ветвь современной прикладной математики. Поэтому весь арсенал методов, разработанных для решения задач МП, может быть применен для решения ЗПР данного класса. Однокритериальные статические ЗПР в условиях риска решаются с использованием методов теории вероятностей и математического программирования. При моделировании задач этого класса находит широкое применение метод статистических испытаний (другое название – метод Монте-Карло). При решении однокритериальных статических ЗПР в условиях неопределенности находит применение ряд математических дисциплин: теория игр, теория минимакса, теория статистических решений. Выбор той или другой дисциплины диктуется природой неопределенных факторов. При решении ЗПР в условиях риска и неопределенности находят также применение экспертные процедуры. Динамические ЗПР, как уже отмечалось, пока находят малое применение в экономических исследованиях, однако за ними большое будущее. В настоящее время наибольшие успехи достигнуты в изучении однокритериальных динамических ЗПР. Однокритериальные динамические детерминированные ЗПР являются предметом изучения специального раздела классической математики – вариационного исчисления и современной прикладной дисциплины – теории оптимальных систем управления. Изучением однокритериальных стохастических динамических ЗПР занимаются современные прикладные дисциплины – теория случайных процессов и статистическая динамика систем управления.

Наименее разработанным в настоящее время видом динамических ЗПР являются динамические ЗПР в условиях неопределенности. Здесь наибольшие успехи достигнуты в отношении динамических ЗПР в условиях конфликтных неопределенностей. Эти задачи являются предметом изучения одной из ветвей теории игр – теории дифференциальных игр. При решении динамических ЗПР в условиях риска и неопределенности также находят применение экспертные процедуры. Наименее разработанным классом ЗПР являются многокритериальные ЗПР, хотя именно они должны иметь наибольшее применение в экономических исследованиях. Действительно, практически любое экономическое исследование столь сложно, что при его изучении и формализации в виде некоторой операции бывает очень трудно, а подчас и невозможно ограничиться одной целью операции и, соответственно, одним критерием оптимальности. В настоящее время теория многокритериальных ЗПР находится в стадии становления. Наибольшие успехи достигнуты здесь в отношении статических детерминированных задач. Большое, место многокритериальные ЗПР занимают в системном анализе, этой современной прикладной дисциплине, предметом изучения которой являются сложные технические и организационно-экономические системы. В системном анализе разработан специальный подход к изучению многокритериальных задач – построение «дерева целей, задач и средств». Широкое применение при решении многокритериальных ЗПР получили экспертные процедуры. В частности, построение «дерева целей» всегда сопряжено с оценкой относительной важности целей с помощью экспертных методов.

Вопрос 3. Классификация методов принятия управленческих решений.

На сегодняшний момент существует очень большое количество методов принятия управленческих решений. Их можно разделить на три категории:

1. Эвристические методы.

2. Качественные методы.

3. Формализованные методы.

Рассмотрим каждую категорию более подробно в разрезе базовых составляющих методов.

Эвристические методы принятия управленческих решений.

В литературе под эвристическими методами понимаются различные процедуры, направленные на сокращение перебора вариантов. Эвристические методы увеличивают вероятность получения работоспособного, но не всегда оптимального решения той или иной задачи.

Ассоциативные методы.

Эти методы основываются на применении в творческом процессе семантических свойств понятий путем использования аналогии их вторичных смысловых оттенков. Основными источниками для генерирования новых идей служат ассоциации, метафоры и случайно выбранные понятия.

К ассоциативным методам относятся:

· метод каталога;

· метод фокальных объектов;

· метод гирлянд случайностей и ассоциаций.

Для разработки большего количества идей решения проблемы прибегают к метафорам. Метафоры служат подсказкой для генерации идеи. Для расширения идей и повышения их оригинальности прибегают к гирляндам ассоциаций.

Если на объект исследования перенести свойства других объектов, резко возрастает число неожиданных альтернатив решений. Эта идея стала основой метода каталога и усовершенствованного метода фокальных объектов. Дальнейшим развитием метода фокальных объектов стал метод гирлянд ассоциаций. Он помогает найти больше количество подсказок для новых идей путем образования ассоциаций.

Метод мозгового штурма.

Метод мозгового штурма (мозговой штурм, мозговая атака) – оперативный метод решения проблемы на основе стимулирования творческой активности, при котором участникам обсуждения предлагают высказывать как можно большее количество вариантов решения, в том числе самых фантастичных. Затем из общего числа высказанных идей отбирают наиболее удачные, которые могут быть использованы на практике.

Этапы и правила мозгового штурма.

Правильно организованный мозговой штурм включает три обязательных этапа. Этапы отличаются организацией и правилами их проведения:

1. Постановка проблемы. Предварительный этап. В начале этого этапа проблема должна быть четко сформулирована. Происходит отбор участников штурма, определение ведущего и распределение прочих ролей участников в зависимости от поставленной проблемы и выбранного способа проведения штурма.

2. Генерация идей. Основной этап, от которого во многом зависит успех всего мозгового штурма. Поэтому очень важно соблюдать правила для этого этапа:

· главное – количество идей, не делайте никаких ограничений;

· полный запрет на критику и любую (в том числе положительную) оценку высказываемых идей, так как оценка отвлекает от основной задачи и сбивает творческий настрой;

· необычные и даже абсурдные идеи приветствуются, комбинируйте и улучшайте любые идеи.

3. Группировка, отбор и оценка идей. Этот этап часто забывают, но именно он позволяет выделить наиболее ценные идеи и дать окончательный результат мозгового штурма. На этом этапе, в отличие от второго, оценка не ограничивается, а наоборот, приветствуется. Методы анализа и оценки идей могут быть очень разными. Успешность этого этапа напрямую зависит от того, насколько одинаково участники понимают критерии отбора и оценки идей.

Для проведения мозговой атаки обычно создают две группы:

· участники, предлагающие новые варианты решения задачи;

· члены комиссии, обрабатывающие предложенные решения.

Различают индивидуальные и коллективные мозговые атаки.

В мозговом штурме участвует коллектив из нескольких специалистов и ведущий. Перед самим сеансом мозгового штурма ведущий производит четкую постановку задачи, подлежащей решению. В ходе мозгового штурма участники высказывают свои идеи, направленные на решение поставленной задачи, причем как логичные, так и абсурдные. Если в мозговом штурме принимают участие люди различных чинов или рангов, то рекомендуется заслушивать идеи в порядке возрастания ранжира, что позволяет исключить психологический фактор «соглашения с начальством».

В процессе мозгового штурма, как правило, вначале решения не отличаются высокой оригинальностью, но по прошествии некоторого времени типовые, шаблонные решения исчерпываются, и у участников начинают возникать необычные идеи. Ведущий записывает или как-то иначе регистрирует все идеи, возникшие в ходе мозгового штурма.

Затем, когда все идеи высказаны, производится их анализ, развитие и отбор. В итоге находится максимально эффективное и часто нетривиальное решение задачи.

Успех мозгового штурма сильно зависит от психологической атмосферы и активности обсуждения, поэтому роль ведущего в мозговом штурме очень важна. Именно он может «вывести из тупика» и вдохнуть свежие силы в процесс.

Изобретателем метода мозгового штурма считается Алекс Осборн, сотрудник рекламного агентства BBD&O. Одним из продолжений метода мозгового штурма является метод синектики.

Метод синектики.

Синектика – методика психологической активизации творчества, предложенная В.Дж. Гордоном. Она является развитием и усовершенствованием метода мозгового штурма. Д. Гордон разработал этот метод решения проблем, когда руководил группой исследования изобретений для Артура Д. Литтла. При синектическом штурме допустима критика, которая позволяет развивать и видоизменять высказанные идеи. Этот штурм ведет постоянная группа. Ее члены постепенно привыкают к совместной работе, перестают бояться критики, не обижаются, когда кто-то отвергает их предложения.

В методе применены четыре вида аналогий – прямая, символическая, фантастическая, личная.

Виды аналогий:

1. При прямой аналогии рассматриваемый объект сравнивается с более или менее похожим аналогичным объектом в природе или технике. Например, для усовершенствования процесса окраски мебели применение прямой аналогии состоит в том, чтобы рассмотреть, как окрашены минералы, цветы, птицы и т.п. или как окрашивают бумагу, кинопленки и т.п.

2. Символическая аналогия требует в парадоксальной форме сформулировать фразу, буквально в двух словах отражающую суть явления. Например, при решении задачи, связанной с мрамором, найдено словосочетание «радужное постоянство», так как отшлифованный мрамор (кроме белого) – весь в ярких узорах, напоминающих радугу, но все эти узоры постоянны.

3. При фантастической аналогии необходимо представить фантастические средства или персонажи, выполняющие то, что требуется по условиям задачи. Например, «хотелось бы, чтобы дорога существовала там, где ее касаются колеса автомобиля».

4. Личная аналогия (эмпатия) позволяет представить себя тем предметом или частью предмета, о котором идет речь в задаче. В примере с окраской мебели можно вообразить себя белой вороной, которая хочет окраситься. Или, если совершенствуется зубчатая передача, то представить себя шестерней, которая крутится вокруг своей оси, подставляя бока соседней шестерне. Нужно в буквальном смысле входить «в образ» этой шестерни, чтобы на себе почувствовать все, что достается ей, и какие она испытывает неудобства или перегрузки. Что дает такое перевоплощение? Оно значительно уменьшает инерцию мышления и позволяет рассматривать задачу с новой точки зрения.

Формализованные методы принятия решений.

Параметрический метод.

Метод заключается в выявлении и устранении физических противоречий, действующих в системе. Под физическим противоречием следует понимать взаимоисключающие требования, предъявляемые к элементу системы, причем один из характеризующих его параметров должен иметь два альтернативных значения. При этом состояние элемента (движение) называется узловым параметром, а характеризуемый им элемент – узловым элементом.

Морфологический метод.

Суть морфологического метода заключается в следующем:

· сначала мы определяем пространство поиска, которое обязательно должно включать в себя искомое решение (схему устройства);

· затем сужаем это пространство, осуществляя поиск этого решения.

В процессе морфологического синтеза мы ищем структуру синтезируемого устройства, проводя поиск на морфологическом множестве.

Балансовые методы.

Балансовые методы – совокупность приемов, позволяющих исследовать и прогнозировать развитие объектов путем сопоставления прихода и расхода вещества, энергии и других потоков. В основе балансовых методов лежит баланс, оценивающий количественно движение потока в пределах анализируемого объекта.

Балансовый метод предполагает сопоставление взаимосвязанных показателей хозяйственной деятельности с целью выяснения и измерения их взаимного влияния, а также подсчета резервов повышения эффективности производства.

Диаграмма Ганта.

Диаграмма Ганта представляет собой отрезки (графические плашки), размещенные на горизонтальной шкале времени. Каждый отрезок соответствует отдельной задаче или подзадаче. Задачи и подзадачи, составляющие план, размещаются по вертикали. Начало, конец и длина отрезка на шкале времени соответствуют началу, концу и длительности задачи. На некоторых диаграммах Ганта также показывается зависимость между задачами. Диаграмма может использоваться для представления текущего состояния выполнения работ – часть прямоугольника, отвечающего задаче, заштриховывается, тем самым отмечается процент выполнения задачи; показывается вертикальная линия, отвечающая моменту «сегодня».

Иначе говоря, диаграмма Ганта – это популярный тип столбчатых диаграмм, который используется для иллюстрации плана, графика работ по какому-либо проекту.

Метод анализа иерархии (МАИ).

МАИ – математический инструмент системного подхода к сложным проблемам принятия решений.

Более подробно метод анализа иерархии будет рассмотрен ниже.

Оптимизационные методы.

По типу математического аппарата различают условную и безусловную оптимизацию. Условная оптимизация – это задачи линейного программирования (ЗЛП).

Линейное программирование – область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т.е. линейных равенств или неравенств, связывающих эти переменные. К задачам линейного программирования приводится широкий круг вопросов планирования экономических и технико-экономических процессов, где ставится задача поиска наилучшего (оптимального) решения; само возникновение и развитие линейного программирования непосредственно связано с экономической проблематикой.

Качественные методы.

Метод Дельфи.

Суть этого метода в том, чтобы с помощью серии последовательных действий – опросов, интервью, мозговых штурмов – добиться максимального консенсуса при определении правильного решения. Анализ с помощью дельфийского метода проводится в несколько этапов, результаты обрабатываются статистическими методами.

Базовым принципом метода является то, что некоторое количество независимых экспертов лучше оценивает и предсказывает результат, чем структурированная группа личностей. Это позволяет избежать открытых столкновений между носителями противоположенных позиций т.к. исключает непосредственный контакт экспертов между собой и, следовательно, групповое влияние, возникающее при совместной работе и состоящее в приспособлении к мнению большинства. Метод Дельфи дает возможность проводить опрос экстерриториально, не собирая экспертов в одном месте (например, посредством электронной почты).

Метод «Дерево решений».

Дерево решений – это графическое изображение процесса принятия решений, в котором отражены альтернативные решения, альтернативные состояния среды, соответствующие вероятности и выигрыши для любых комбинаций альтернатив и состояний среды.

Метод сценариев.

Метод сценариев получил очень большое распространение в современном мире. Используется во всех отраслях экономики, как для открытия новых компаний, так и для синтеза действующих компаний. Наиболее часто можно увидеть применение данного метода при составлении различных прогнозов для финансово-хозяйствующего субъекта (к примеру, при прогнозировании продаж).

Как правило, данный метод подразумевает составление трех сценариев:

a) пессимистического;

b) реального;

c) оптимистического.

Вопрос 4. Предпосылки появления систем поддержки принятия решений (СППР).

Ситуацию с корпоративной информацией, складывающуюся в настоящее время на большинстве предприятий, можно сравнить с сокровищем, которое лежит под ногами, но которое никто не может извлечь. По данным Gartner Group, большая часть корпоративной информации – 90 % – лежит невостребованной и никак не анализируется. Между тем многие из проблем, которые возникают в текущей деятельности предприятия и которые требуют оперативного решения, не являются для него абсолютно новыми. Как правило, предприятие уже когда-то сталкивалось с похожей ситуацией, и в этой связи были приняты определенные управленческие решения, которые привели к соответствующим результатам. Этот опыт (позитивный или негативный) может оказаться очень ценным при решении проблем, стоящих перед предприятием в настоящий момент.

Подобное положение с очевидностью говорит о том, что необходимы технологии, которые бы позволили анализировать накопленную информацию и предоставили бы возможность оперативно принимать максимально взвешенные решения.

Руководители предприятий сегодня осторожно относятся к проектам внедрения информационных систем, все больше задумываясь над тем, куда они вкладывают деньги и какой результат получат от этих вложений. Многие компании имеют негативный опыт внедрения подобных систем, а инвесторы не получают от реализации таких проектов ожидаемого эффекта. Одной из причин, как представляется, оказывается размытость цели построения информационной системы предприятия.

Целью построения каждой информационной системы должно быть обеспечение максимально прозрачного и эффективного управления бизнесом, то есть предоставление управляющему звену возможности проводить текущую оценку состояния бизнеса, формулировать и описывать бизнес-цели, определять методы и пути достижения поставленных задач.

Для этого, с одной стороны, система должна снабжаться максимально полной, актуальной, качественной и согласованной информацией, а с другой – обеспечивать максимально эффективный, быстрый и многоаспектный анализ данных.

Анализировать всю накопленную корпоративную информацию и учитывать результаты такого анализа в процессе принятия бизнес-решений позволяют так называемые Системы поддержки принятия решений – СППР (Decision Support Systems, DSS). А применяемые технологии именуются OLTP – On-Line Transaction Processing.

Если попытаться коротко сформулировать роль таких технологий в системе управления предприятием, то СППР – это инструмент менеджеров предприятия, предназначенный для решения следующих ключевых задач:

· оценка текущего состояния бизнеса предприятия;

· формулирование и описание бизнес-целей;

· определение методов и способов достижения поставленных бизнес-целей.

Эти технологии уже много лет применяются на Западе и становятся все более актуальными в России.

OLTP- и OLAP-технологии.

Задачи OLTP-системы – это быстрый сбор и наиболее оптимальное размещение информации в базе данных, а также обеспечение ее полноты, актуальности и согласованности. Однако такие системы не предназначены для максимально эффективного, быстрого и многоаспектного анализа.

Разумеется, по собранным данным можно строить отчеты, но это требует от бизнес-аналитика или постоянного взаимодействия с IT-специалистом, или специальной подготовки в области программирования и вычислительной техники.

Мировая индустрия давно знакома с этой проблемой, и вот уже почти 30 лет существуют OLAP-технологии, которые и предназначены именно для того, чтобы бизнес-аналитики имели возможность оперировать с накопленными данными, непосредственно участвовать в их анализе. Подобные аналитические системы противоположны OLTP-системам в том плане, что они устраняют информационную избыточность («сворачивают» информацию). Вместе с тем очевидно, что именно избыточность первичной информации определяет эффективность анализа. СППР, объединяя эти технологии, дают возможность решать целый ряд задач.

· Аналитические задачи: вычисление заданных показателей и статистических характеристик бизнес-процессов на основе ретроспективной информации, находящейся в хранилищах данных.

· Визуализация данных: представление всей имеющейся информации в удобном для пользователя графическом и табличном виде.

· Получение новых знаний: определение взаимосвязи и взаимозависимости бизнес-процессов на основе существующей информации (проверка статистических гипотез, кластеризация, нахождение ассоциаций и временных шаблонов).

· Имитационные задачи: математическое моделирование поведения сложных систем в течение произвольного периода времени. Иными словами, это задачи, связанные с необходимостью ответить на вопрос «Что будет, если?..».

· Синтез управления: определение допустимых управляющих воздействий, обеспечивающих достижение заданной цели.

· Оптимизационные задачи: интеграция имитационных, управленческих, оптимизационных и статистических методов моделирования и прогнозирования.

Менеджеры предприятия, использующие инструментальные средства OLAP-технологии, даже без специальной подготовки могут самостоятельно и оперативно получать всю необходимую для исследования закономерностей бизнеса информацию, причем в самых различных комбинациях и срезах бизнес-анализа. Бизнес-аналитик имеет возможность видеть перед собой список измерений и показателей бизнес-системы. При столь простом интерфейсе аналитик может строить любые отчеты, перестраивать измерения (скажем, делать кросс-таблицы – накладывать одно измерение на другое). Кроме этого, он получает возможность создавать свои функции на базе существующих показателей, проводить анализ «что, если» – получать результат, задавая зависимости каких-либо показателей бизнес-функций или бизнес-функцию от показателей. При этом максимальный отклик любого отчета не превышает 5 секунд.

Структура СППР.

Система строится на основе четырех ключевых компонентов:

· Информационных Хранилищ Данных;

· ETL (Extracting Transformating and Loading) – средств и методов извлечения, обработки и загрузки данных;

· OLAP – многомерной базы данных и средств анализа;

· Data Mining – средств извлечения данных.

При этом Технология Информационных Хранилищ Данных обеспечивает:

· быструю обработку поступающих запросов;

· интеграцию распределенных данных;

· интеграцию внутренних и внешних данных;

· устранение ненужной информации;

· агрегирование (вычисление сумм, средних показателей);

· преобразование типов данных, структур хранения;

· приведение данных к одному моменту времени.

Хранилище Данных строится на основе OLTP-базы данных, а также различных разнородных источников информации. Таким образом, система сбора информации представляет собой централизованный импорт данных из существующих учетных систем.

Когда данные импортируются в Хранилище Данных, они подвергаются некоторой первичной обработке, обеспечивающей эффективность последующего анализа: производится очистка данных, структурирование по времени, агрегирование, фильтрация и ряд других операций.

Все это необходимо для того, чтобы бизнес-аналитик не только оперировал данными оперативного учета (так называемая оперативная отчетность), но имел возможность производить полнофункциональный анализ, строить прогнозы и при этом работать с системой в тех бизнес-терминах, которые он использует в повседневной работе.

Еще одна задача Хранилища Данных – интеграционная, то есть предоставление возможности объединить разнородные источники информации в единое информационное пространство, с которым удобнее работать и которым легче управлять. Во многих компаниях установлены разнородные системы, отвечающие (причем очень эффективно) за выполнение тех или иных задач. Хранилище Данных обеспечивает интеграцию этих источников информации и одновременно «разгружает» учетные системы, освобождая их от построения отчетов.

Кроме того, на предприятиях существует большой объем нерегламентированной информации, которую также необходимо подвергать анализу. Это информация, которая приходит от руководящих и регулирующих органов и не поступает в базу данных предприятия, а также информация, получаемая из Интернета, и любые другие существенные для бизнеса данные. Хранилище позволяет собирать эту информацию и производить ее дальнейший анализ средствами OLAP.

OLAP – это технология анализа данных, включающая возможности аналитической обработки информации из разных источников (файлов, баз данных и программных приложений); определения скрытых зависимостей между данными и построения объективной картины информации по различным срезам; представления необходимых для прогнозирования данных в виде, простом и понятном для всех, кто занимается управлением.

Data Mining – технология извлечения данных, позволяющая осуществлять поиск общих закономерностей в больших объемах данных. С помощью технологии Data Mining решаются следующие задачи:

· применение правила «если … , то … » с использованием коэффициентов уверенности;

· определение характеристик ненадежного клиента;

· выявление перспективных клиентов;

· сохранение существующих клиентов;

· отбор кандидатов для рассылки новых предложений;

· определение стратегии продаж;

· составление и оценка системы скидок.

Необходимо отметить, что OLAP-технологии в целом очень гармонично интегрируются с другими технологиями построения информационных систем. Например, одновременно с внедрением CRM-системы можно установить и OLAP-систему как средство обработки информации, которую CRM-система позволяет накапливать. Более того, сейчас и в состав многих ERP-систем входят OLAP-решения. Например, Oracle Application содержит такие продукты, как Oracle Financial Analyzer, Oracle Sales Analyzer.

Литература по теме:

Основная литература:

1. Литвак Б.Г. Управленческие решения: Учебник. – М.: МФПУ «Синергия», 2012. – 512 с. – (Академия бизнеса).

2. Литвак Б.Г. Управленческие решения: Практикум. – М.: МФПУ «Синергия», 2012. – 448 с. – (Академия бизнеса).

Дополнительная литература:

1. Андрейчиков А.В., Андрейчикова О.Н. Анализ, синтез, принятие решений в экономике. – М.: Финансы и статистика, 2007. – 368 с.

2. Ларичев О.И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах: Учебник. – М.: Логос, 2008. – 392 с.

3. Смирнов Э.А. Разработка управленческих решений. – М.: ИНФРА-М, 2008. – 272 с.

4. Фатхутдинов Р.А. Разработка управленческого решения: Учеб. пособие. – М.: Бизнес-школа, Интел-Синтез, 2007. – 272 с.

Тема 3. Разработка управленческих решений в условиях определенности

Цели и задачи:

Цель изучения данной темы – получение общетеоретических знаний о методах разработки и принятия УР в условиях определенности.

Задачи изучения данной темы:

· ознакомление с постановкой задачи принятия решений в общем теоретическом и математическом виде;

· изучение методов принятия решений в условиях определенности;

· изучение метода анализа иерархий.

Вопросы темы:

1. Проблема планирования деятельности фирмы.

2. Методы решения задач планирования в условиях полной определенности.

3. Иерархическое представление проблемы.

Вопрос 1. Проблема планирования деятельности фирмы.

Проблема планирования деятельности фирмы заключается в определении различных альтернатив действий и выборе оптимальной альтернативы, т.е. такой, которая позволяет получить наилучший результат в достижении поставленной цели. В качестве альтернатив могут выступать новые целевые области (товарные рынки), виды выпускаемой продукции, инвестиции в различные сферы деятельности фирмы и т.д. Как правило, они не могут быть реализованы одновременно. Целенаправленный выбор среди подобных альтернатив представляет собой принятие управленческого решения.

Реализация (осуществление) любой возможной альтернативы ведет к одному или нескольким последствиям (результатам). Ожидаемыми результатами могут быть выручка от реализации товаров, издержки производства, доля удовлетворения спроса, прибыль, затраты на продвижение товара, доля рынка и др.

На значение результата обычно оказывают влияние разнообразные факторы, которые не подвержены или почти не подвержены влиянию со стороны ЛПР. Возможное положение дел, не зависящее напрямую от воздействия руководства фирмы, называется ситуацией внешней или окружающей среды. Состояние внешней среды складывается, как правило, в результате имеющейся политической обстановки (стабильная, нестабильная), поведения конкурирующих фирм (реактивное, нереактивное поведение), социально-экономических условий (платежеспособного спроса, правительственного регулирования экономики и т.д.). Состояния внешней среды в теории принятия решений называют обычно гипотезами.

Каждой реализуемой альтернативе соответствуют некоторые состояния окружающей среды . Ожидаемый результат e_ij при выборе альтернативы A_i и принятии гипотезы Z_j получается, если применить функцию предпочтения или, как чаще всего говорят, функцию полезности f, т.е.:

Предполагается, что ЛПР известны получаемые благодаря ей закономерности. Значения функции f наглядно представляются в виде так называемой матрицы ожидаемых результатов. При этом могут задаваться вероятности появления ситуаций внешней среды (гипотез) , которые при принятии решений считаются рисками. Таким образом, проблема планирования может быть сведена к получению необходимой информации, размещению ее в виде таблиц (например, в виде табл. 1), представляющих собой по существу основные модели задач теории принятия решений, и выбору оптимальной альтернативы.

Таблица 1.

Матрица описания задач принятия решений

Альтернативы, A_i	Состояния внешней среды (гипотезы)
Альтернативы, A_i	Z₁	Z₂	…	Z_n
А₁	e₁₁	e₁₂	…	e_1n
А₂	e₂₁	e₂₂	…	e_2n
…	…	…	…	…
A_m	e_m1	e_m2	…	e_mn
Вероятности гипотез, p_j	p₁	p₂	…	p_n

Альтернатива A_i считается в общем случае доминирующей, если не существует никакой другой альтернативы со значением и (для наименьшей величины, соответствующей j).

Здесь e_kj означает ожидаемый результат от применения альтернативы A_k при наступлении состояния внешней среды Z_j. Если в матрице решений имеется доминирующая альтернатива, то она и выбирается в качестве планового решения. Однако, как правило, доминирующие альтернативы отсутствуют и, кроме того, решение приходится принимать в условиях риска и неопределенности. Здесь нужны специальные принципы принятия решений, или решающие правила, или критерии принятия решений, которые используются иногда как синонимы.

Итак, мы имеем задачу принятия решений (ПР). Все задачи ПР группируются в зависимости от набора классификационных признаков. Существует несколько подходов к классификации задач принятия решений (ЗПР). Однако большинство из них опирается на следующие признаки: характер субъекта (ЛПР), содержание ЗПР, количество целей, влияние времени, значимость решений. Каждый из признаков включает несколько параметров классификации ЗПР.

Особый интерес представляет признак «характер субъекта ПР», который описывает степень информированности ЛПР о проблемной ситуации и указывает конкретный тип ЛПР. Ниже рассмотрим методы принятия решений:

a) в условиях полной определенности, когда известны все составляющие и характеристики проблемы планирования;

b) в условиях вероятностной определенности (риска);

c) в условиях неопределенности.

На первом этапе планирования происходит упорядочение имеющейся (полученной) информации, которая размещается в соответствующих таблицах. Следует заметить, что для каждого типа задач принятия решений создается своя система подготовки информации.

Рис. 1. Классификация ЗПР по уровням и признакам группирования

Вопрос 2. Методы решения задач планирования в условиях полной определенности.

В данном случае необходимо различать однокритериальные и многокритериальные методы выбора плановых решений.

1. Однокритериальные методы выбора. Считается известным:

· исходное множество альтернатив ;

· оценки результатов выбираемых альтернатив f(A_i);

· критерий выбора или .

Следовательно, выбор характеризуется однозначной связью между принятым решением A_i и его результатом f(A_i). В процессе решения задачи определяется альтернатива A*, для которой f(A*) = max f(A_i) или f(A*) = min f(A_i).

2. Многокритериальные методы выбора. В достаточно большом количестве практических случаев принятия решений при планировании действий приходится учитывать не один, а несколько критериев. Не умаляя общности, можно считать, что все критерии стремятся к максимуму, так как если некоторые критерии минимизируются, то путем умножения их на (-1) они будут стремиться к максимуму, причем решение при этом не изменяется. Матрица исходных данных принятия решений имеет вид (табл. 2).

Если в табл. 2 находится доминирующая альтернатива, то проблемы выбора как таковой не существует, а именно данная альтернатива и принимается в качестве планового решения.

Таблица 2.

Матрица исходных данных для многокритериальных методов выбора

Альтернативы, A_i	Критерии (цели)
Альтернативы, A_i	Z₁	Z₂	…	Z_n
А₁	e₁₁	e₁₂	…	e₁_n
А₂	e₂₁	e₂₂	…	e₂_n
…	…	…	…	…
A_m	e_m₁	e_m₂	…	e_mn

Однако, как было отмечено ранее, доминирующие стратегии на практике встречаются довольно редко. Поэтому приходится применять методы многокритериального выбора, причем решение должно быть наилучшим в определенном смысле. Итак, выделение существенных для модели рассматриваемой экономической системы показателей качества альтернатив выбора, соответствующих поставленным целям, приводит к задаче векторной оптимизации, которая заключается в нахождении максимума вектор-функции:

где

D – область допустимых решений модели.

В случае многокритериальной оптимизации возникают три проблемы. Первая проблема связана с выбором принципа оптимальности. В математическом отношении эта проблема эквивалентна задаче упорядочения векторных множеств, а выбор принципа оптимальности – выбору отношений порядка. Вторая проблема связана с нормализацией векторного критерия F(х). Дело в том, что частные критерии имеют различные единицы измерения, поэтому их необходимо привести к единому масштабу измерения, т.е. нормализовать (обычно приводят к безразличным величинам). Третья проблема связана с учетом приоритета (степени важности) частных критериев. Часто для учета приоритета вводится вектор распределения важности или значимости критериев .

В задаче многокритериального выбора решение почти всегда ищется в области компромиссов или в области решений. Известен целый ряд методов решения многокритериальных задач, которые можно разбить на четыре группы:

1. Сведение многих критериев к одному путем введения весовых коэффициентов для каждого критерия (более важный критерий получает больший вес).

2. Минимизация максимальных отклонений от наилучших значений по всем критериям.

3. Оптимизация одного критерия (почему-либо признанного наиболее важным), а остальные критерии выступают в роли дополнительных ограничений.

4. Упорядочение (ранжирование) множества критериев и последовательная оптимизация по каждому из них.

В рассматриваемой постановке множество допустимых планов есть совокупность альтернатив , а значения критериев равны

Покажем применение некоторых методов многокритериальной оптимизации к решению задач планирования в системе управления фирмой.

Метод равномерной оптимизации.

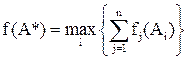(1)

Он применяется, если глобальное качество альтернативы представляет собой сумму локальных (частных) качеств и, кроме того, все критерии имеют одну и ту же единицу измерения, например денежное выражение либо безразмерные величины. Главный недостаток метода – это возможность компенсации малых значений некоторых критериев достаточно большими значениями других.

Метод справедливого компромисса.

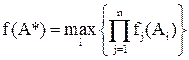(2)

Он применяется, во-первых, потому что существуют разнообразные схемы, приводящие к такому методу, во-вторых, потому что имеется тесная связь с решением в некооперативных играх.

Метод свертывания критериев.

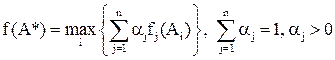(3)

Здесь каждому из критериев приписываются весовые коэффициенты , определяющие предпочтения ЛПР.

Метод главного критерия.

. (4)

Здесь f₁(х) – главный (наиболее важный из всех для ЛПР) критерий, d_j– нижняя граница j-го критерия, устанавливаемая ЛПР.

Метод идеальной точки.

Суть метода заключается в поиске плана, удовлетворяющего условию равномерного сжатия:

(5)

Метод последовательных уступок (или пороговых значений).

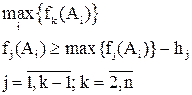где

h_j – уступка по критерию f_j(x), т.е. величина, на которую ЛПР согласен уменьшить значение данного критерия по сравнению с его максимальным значением.

Метод группировки критериев.

Суть метода заключается в том, что множество критериев, значения которых предварительно вычислены на некотором оптимальном (по Парето) плане x°, разбивается на три группы. Первая группа включает критерии, значения которых могут быть уменьшены по сравнению со значениями, вычисленными на плане x°. Вторая группа состоит из критериев, значения которых желательно увеличить. Третья группа включает критерии, значения которых не хотелось бы уменьшать по сравнению с достигнутыми на плане x°. Далее отыскивается план уже в новой системе ограничений, который позволяет максимально увеличить значение критерия второй группы.

Так как критерии могут иметь различные масштабы и шкалы измерения, то прежде, чем приступить к решению многокритериальной задачи, их необходимо привести к одной единице измерения (обычно к безразмерному виду). Этот процесс называется нормализацией. Существуют различные методы нормализации. Предлагается следующий способ получения безразмерной формы критериев:

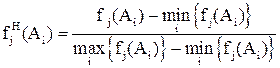(6)

где

Рассмотрим следующую многокритериальную задачу планирования. Пусть фирма имеет возможность реализовывать свои товары на 4-х различных рынках (альтернативы А₁, А₂, А₃, А₄). При этом ставятся одновременно следующие цели: минимизация затрат на рекламу, завоевание максимальной доли рынка и максимальный объем продаж в течение планируемого периода. Исходные данные приведены в табл. 3.

Таблица 3.

Исходные данные многокритериальной задачи (пример)

Альтернативы, рынки	Цели (критерии)
Альтернативы, рынки	затраты на рекламу, тыс. ден. ед., f₁	доля рынка, %, f₂	объем продаж, тыс. ден. ед., f₃
А₁	7	45	90
А₂	5	40	85
А₃	9	50	80
А₄	6	45	83

Значения критериев даны в различных единицах измерения, поэтому согласно формуле (6) приведем их к безразмерному виду:

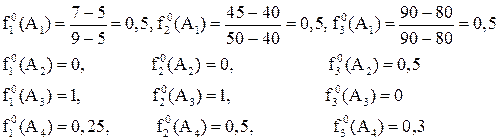
Так как критерий f₁ минимизируется, то для того, чтобы все критерии стремились к максимуму, умножим безразмерные величины критерия f₁ на (-1) и сформируем табл. 4.

Таблица 4.

Преобразованные исходные данные (пример)

Альтернативы	Цели (критерии)
Альтернативы	f₁	f₂	f₃
А₁	-0,5	0,5	1
А₂	0	0	0,5
А₃	-1	1	0
А₄	-0,25	0,5	0,3

Метод равномерной оптимальности.

В соответствии с (1) имеем:

Альтернативы	Цели (критерии)			Критерий
Альтернативы	f₁	f₂	f₃	Критерий
А₁	-0,5	0,5	1	-0,5 + 0,5 + 1 = 1
А₂	0	0	0,5	0,5
А₃	-1	1	0	0
А₄	-0,25	0,5	0,3	-0,25 + 0,5 + 0,3 = 0,55

Следовательно, согласно принципу равномерной оптимальности, предприятию выгоднее работать на рынке А₁

Метод справедливого компромисса.

Чтобы воспользоваться данным методом, избавимся от отрицательности критерия f₁, добавив константу, например 1. Тогда значения первого критерия будут равны:

На основании (2) имеем:

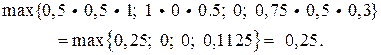
Альтернативы	Цели (критерии)			Критерий
Альтернативы	f₁	f₂	f₃	Критерий
А₁	-0,5 + 1 = 0,5	0,5	1	0,5 * 0,5 1 = 0,25*
А₂	0 + 1 = 1	0	0,5	1 * 0 * 0,5 = 0
А₃	-1 + 1 = 0	1	0	0
А₄	-0,25 + 1 = 0,75	0,5	0,3	0,75 * 0,5 * 0,3 = 0,1125

Результат получился аналогичный предыдущему, а именно выгоднее работать на рынке А₁.

Метод свертывания критериев.

Сначала положим следующие значения весовых коэффициентов: .Тогда функции свертки в соответствии с (3) будут равны:

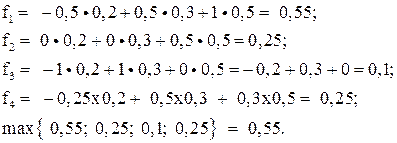
Альтерна-тивы	Цели (критерии)			Критерий
Альтерна-тивы	f₁	f₂	f₃	Критерий
А₁	-0,5	0,5	1	-0,5 * 0,2 + 0,5 * 0,3 + 1 * 0,5 = 0,55
А₂	0	0	0,5	0 * 0,2 + 0 * 0,3 + 0,5 * 0,5 = 0,25
А₃	-1	1	0	-1 * 0,2 + 1 * 0,3 + 0 * 0,5 = 0,1
А₄	-0,25	0,5	0,3	-0,25 * 0,2 + 0,5 * 0,3 + 0,3 * 0,5 = 0,25

При таком значении коэффициентов значимости критериев выгоднее работать на рынке A₁

Если доложить , то получим:

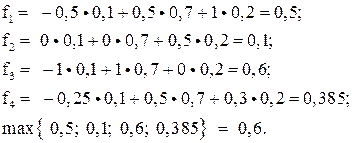
Альтер-нативы	Цели (критерии)			Критерий
Альтер-нативы	f₁	f₂	f₃	Критерий
А₁	-0,5	0,5	1	-0,5 * 0,1 + 0,5 * 0,7 + 1 * 0,2 = 0,5
А₂	0	0	0,5	0 * 0,1 + 0 * 0,7 + 0,5 * 0,2 = 0,1
А₃	-1	1	0	-1 * 0,1 + 1 * 0,7 + 0 * 0,2 = 0,6
А₄	-0,25	0,5	0,3	-0,25 * 0,1 + 0,5 * 0,7 + 0,3 * 0,2 = 0,385

Таким образом, если приоритет отдается доле рынка (), то фирме имеет смысл работать на рынке А₃.

Если же фирма находится в затруднительном положении с точки зрения средств, выделяемых на рекламу, другими словами, для нее в данный момент самым важным является минимизация затрат на рекламу, то коэффициенты значимости могут быть, например, выбраны такие: ;

Следовательно, в такой ситуации лучше всего работать на рынке А₂.

Если задать весовые коэффициенты , то

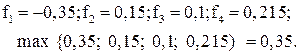
При таких значениях весовых коэффициентов выгоднее работать на рынке А₁.

Приведем два последних варианта решений в следующей таблице:

Альтерна-тивы	Цели (критерии)			Критерий
	Цели (критерии)
	f₁	f₂	f₃
А₁	-0,5	0,5	1	-0,25	0,35
А₂	0	0	0,5	0,05	0,15
А₃	-1	1	0	-0,7	0,1
А₄	-0,25	0,5	0,3	-0,12	0,215

Метод главного критерия.

Пусть главный критерий f₁ – затраты на рекламу, а остальные критерии выступают в роли ограничений, причем доля рынка должна быть не меньше 45 %, а объем продаж не меньше 85 тыс. ден. ед. Тогда в соответствии с (4) минимальное значение главного критерия f₁ равно 5 тыс. ден. ед. и соответствует альтернативе А₂ однако с учетом ограничения на долю рынка следует выбрать альтернативу A₄, но так как еще требуется, чтобы объем продаж был не меньше 85 тыс. ден. ед., то наилучшей альтернативой в этом случае будет рынок A₁.

f₁– главный критерий, f₂ 45 %, f₃ 85 тыс. ден. ед.

Альтернативы, рынки	Цели (критерии)
Альтернативы, рынки	затраты на рекламу, тыс. ден. ед., f₁	доля рынка, %, f₂	объем продаж, тыс. ден. ед., f₃
А₁	7	45	90
А₂	5=min	40	85
А₃	9	50	80
А₄	6	45	83

Метод идеальной точки (критерий равномерного сжатия соответствует принципу Сэвиджа). Определим сначала максимальные значения критериев. А именно Матрица отклонений значений критериев от наилучших значений имеет вид:

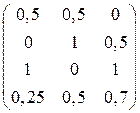
Максимальные отклонения по каждой из 4-х альтернатив имеют следующие значения: 0,5; 1; 1; 0,7. Выберем минимальное из этих отклонений:

	Цели (критерии)			Отклонения от max			Max отклонения
	f₁	f₂	f₃				Max отклонения
А₁	-0,5	0,5	1=	0 – (-0,5) = 0,5	1 – 0,5 = 0,5	1 – 1 = 0	0,5 = min
А₂	0 =	0	0,5	0	1 – 0 = 1	1 – 0,5 = 0,5	1
А₃	-1	1=	0	0 – (-1) = 1	1 – 1 = 0	1 – 0 = 1	1
А₄	-0,25	0,5	0,3	0 – (-0,25) = 0,25	1 – 0,5 = 0,5	1 – 0,3 = 0,7	0,7

Минимальное значение 0,5 соответствует альтернативе A₁ – следовательно, используя данный метод, получим решение, которое рекомендует фирме планировать работу на рынке A₁.

Вопрос 3. Иерархическое представление проблемы.

Метод анализа иерархий (далее МАИ), как было сказано выше, – это математический инструмент системного подхода к сложным проблемам принятия решений. Основное применение при проведении оценки МАИ находит при осуществлении процедуры согласования полученных результатов по затратному, сравнительному и доходному подходу и расчете итоговой стоимости оцениваемого объекта. Рассмотрим методологию данного математического инструментария более подробно.

МАИ не предписывает лицу, принимающему решение, какого-либо правильного решения проблемы, а позволяет ему в интерактивном режиме найти такой альтернативный вариант, который наилучшим образом согласуется с пониманием указанным лицом сути проблемы и требованиями к ее решению. МАИ позволяет понятным и рациональным образом структурировать сложную проблему принятия решений в виде иерархии, а также сравнить и выполнить количественную оценку альтернативных вариантов решения.

Анализ проблемы принятия решений в МАИ начинается с построения иерархической структуры, которая включает цель, критерии, альтернативы и другие рассматриваемые факторы, влияющие на выбор. Эта структура отражает понимание проблемы лицом, принимающим решение. Каждый элемент иерархии может представлять различные аспекты решаемой задачи, причем во внимание могут быть приняты материальные и нематериальные факторы, измеряемые количественные параметры и качественные характеристики, объективные данные и субъективные экспертные оценки. Следующим этапом анализа является определение приоритетов, представляющих относительную важность или предпочтительность элементов построенной иерархической структуры, с помощью процедуры парных сравнений. Безразмерные приоритеты позволяют обоснованно сравнивать разнородные факторы, что является отличительной особенностью МАИ. На заключительном этапе анализа выполняется синтез (линейная свертка) приоритетов на иерархии, в результате которой вычисляются приоритеты альтернативных решений относительно главной цели. Лучшей считается альтернатива с максимальным значением приоритета.

Рассмотрим каждый этап МАИ более подробно:

Представление проблемы в виде иерархии.

Вершиной иерархии является главная цель; элементы нижнего уровня представляют множество вариантов достижения цели (альтернатив); элементы промежуточных уровней соответствуют критериям или факторам, которые связывают цель с альтернативами. Существуют специальные термины для описания иерархической структуры МАИ. Каждый уровень иерархии состоит из узлов. Элементы, исходящие из узла, принято называть его «детьми» (дочерними элементами). Элементы, из которых исходит узел, называются родительскими. Группы элементов, имеющие один и тот же родительский элемент, называются группами сравнения. Родительские элементы альтернатив, как правило, исходящие из различных групп сравнения, называются покрывающими критериями. Вид любой иерархии МАИ будет зависеть не только от объективного характера рассматриваемой проблемы, но и от знаний, суждений, системы ценностей, мнений, желаний и т.п. участников процесса. Опубликованные описания применений МАИ часто включают в себя различные схемы и объяснения представленных иерархий. Последовательное выполнение всех шагов МАИ предусматривает возможность изменения структуры иерархии с целью включения в нее вновь появившихся или ранее не считавшихся важными критериев и альтернатив.

Иерархия является полной, если каждый элемент заданного уровня является критерием для всех элементов нижнего уровня (рис. 2).

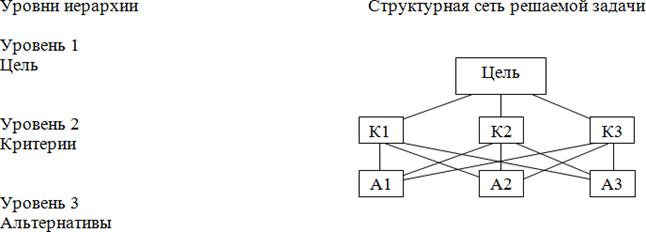
Рис. 2. Полная доминантная иерархия

Определение приоритетов критериев.

После иерархического представления задачи необходимо установить приоритеты критериев и оценить каждую из альтернатив по выбранным критериям, определив наиболее важную их них.

Приоритеты – это числа, которые связаны с узлами иерархии. Они представляют собой относительные веса элементов в каждой группе. Подобно вероятностям, приоритеты – безразмерные величины, которые могут принимать значения от нуля до единицы. Чем больше величина приоритета, тем более значимым является соответствующий ему элемент. Сумма приоритетов элементов, подчиненных одному элементу вышестоящего уровня иерархии, равна единице. Приоритет цели по определению равен 1,0.

В МАИ элементы сравниваются попарно по отношению к их влиянию на общую для них характеристику.

Парные сравнения приводят к записи характеристик сравнений в виде квадратной таблицы чисел, т.е. матрицы.

Сравнивая набор критериев друг с другом, получим обратно симметричную матрицу, т.е. имеет место свойство:

где

индексы i и j – номер строки и номер столбца, на пересечении которых стоит элемент.

При сравнении элемента с самим собой имеем равную значимость, так что на пересечение строки и столбца с одинаковыми номерами заносим единицу. Поэтому главная диагональ будет состоять из единиц.

Таким образом, матрица парных сравнений имеет вид:

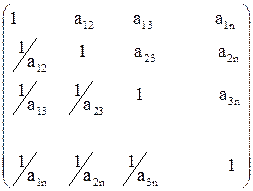
Когда задача представлена в виде иерархической структуры, матрица составляется для попарного сравнения критериев на втором уровне по отношению к общей цели, расположенной на первом уровне. Такие же матрицы должны быть построены для парных сравнений каждой альтернативы на третьем уровне по отношению к критериям второго уровня и т.д., в зависимости от количества уровней.

Матрица составляется следующим образом. В левом верхнем углу записывается цель или критерий, по отношению к которым будет проводиться сравнение; в левом столбце и верхней строке необходимо перечислить сравниваемые элементы. Для иерархии, приведенной на рис. 2, потребуется построить четыре матрицы – одну для второго уровня и три для третьего. Эти матрицы представлены в табл. 5 и 6.

Таблица 5.

Матрица второго уровня

Цель	К1	К2	К3
К1
К2
К3

Таблица 6.

Матрицы третьего уровня

К1	А1	А2	А3
А1
А2
А3

К2	А1	А2	А3
А1
А2
А3

К3	А1	А2	А3
А1
А2
А3

Для проведения субъективных парных сравнений в МАИ разработана шкала относительной важности, представленная в табл. 7.

Таблица 7.

Шкала относительной важности

Интенсивность относительной важности	Определение	Объяснение
1	Равная важность	Равный вклад двух критериев в цель
3	Умеренное превосходство одного над другим	Опыт и суждения дают легкое превосходство одной альтернативы над другой
5	Существенное или сильное превосходство	Опыт и суждения дают сильное превосходство одного критерия над другим
7	Значительное превосходство	Одному из критериев дается настолько сильное предпочтение, что оно становится практически значительным
9	Очень сильное превосходство	Очевидность превосходства одного критерия над другим подтверждается наиболее сильно
2, 4, 6, 8	Промежуточные решения между двумя соседними суждениями	Применяется в компромиссных случаях
Обратные величины приведенных выше чисел	Если при сравнении одного критерия с другим получено одно из вышеуказанных чисел, то при сравнении второго критерия с первым получаем обратную величину

При проведении попарных сравнений задаются следующие вопросы:

· Какая из альтернатив важнее или имеет большее воздействие на цель?

· Какая из альтернатив более вероятна?

· Какая из альтернатив предпочтительнее?

· Какой из критериев более важен?

· Какая из альтернатив более желательна по отношению к определенному критерию?

· Какой из сценариев более вероятен?

Когда возникают споры, применяют геометрическое среднее разных оценок в качестве общей оценки суждений:

Синтез приоритетов.

После построения иерархии и определения величин парных субъективных суждений следует этап, на котором иерархическая декомпозиция и относительные суждения объединяются для получения осмысленного решения многокритериальной задачи принятия решений.

Локальные приоритеты.

Из групп парных сравнений формируется набор локальных критериев, которые выражают относительное влияние элементов на элемент, расположенный на уровень выше.

Для определения относительной ценности каждого элемента необходимо найти геометрическое среднее и с этой целью перемножить n элементы каждой строки и из полученного результата извлечь корни n-й степени (7). Полученные числа необходимо нормализовать.

(7)

Для нормализации полученных чисел определяем нормирующий множитель r.

(8)

И каждое из чисел ω_i делим на r.

(9)

В результате получаем вектор приоритетов:

(10)

где индекс «2» означает, что вектор приоритетов относится ко второму уровню иерархии.

Согласованность локальных приоритетов.

Любая матрица суждений в общем случае является не согласованной. Действительно, в практических задачах согласованность нарушается, поскольку человеческие суждения нельзя выразить точной формулой.

Когда отклонения от согласованности превышают установленные пределы, возникает необходимость определения индекса согласованности и отношения согласованности.

Индекс согласованности (ИС) в каждой матрице и для всей иерархии может быть выражен следующим способом.

Определяется сумма каждого j-го столбца матрицы суждений.

(11)

Затем полученный результат умножается на j-ю компоненту нормализованного вектора приоритетов q₂, т.е. сумма суждений первого столбца – на первую компоненту, сумма суждений второго столбца – на вторую и т.д.

(12)

Сумма чисел р_j отражает пропорциональность предпочтений, чем ближе эта величина к n (числу объектов и видов действия в матрице парных сравнений), тем более согласованны суждения

(13)

Отклонение от согласованности выражается индексом согласованности:

(14)

Для определения того, насколько точно ИС отражает согласованность суждений, его необходимо сравнить со случайным индексом согласованности (далее СИ), который соответствует матрице со случайными суждениями, выбранными из шкалы

при условии равной вероятности выбора любого из приведенных чисел.

В табл. 8 приведены средние значения случайного индекса согласованности (СИ) для случайных матриц суждений разного порядка.

Таблица 8.

Средние значения СИ для случайных матриц суждений разного порядка

Размер матрицы	Среднее значение СИ
1	0,00
2	0.00
3	0.58
4	0.90
5	1.12
6	1.24
7	1.32
8	1.41
9	1,45
10	1,49
11	1,51
12	1,48
13	1,56
14	1,57
15	1,59

Отношение ИС к среднему значению СИ для матрицы того же порядка называется отношением согласованности (ОС):

(15)

Значение ОС меньше или равное 0,10 считается приемлемым.

Синтез альтернатив.

Векторы приоритетов и отношения согласованности определяются для всех матриц суждений, начиная со второго уровня вниз.

Для определения приоритетов альтернатив необходимо локальные приоритеты умножить на приоритет соответствующего критерия на вышестоящем уровне и найти суммы по каждому элементу в соответствии с критериями, на которые воздействует этот элемент.

Примем следующие обозначения:

q_3k – вектор приоритетов k-й матрицы, расположенной на третьем уровне;

q_3ki – i-й элемент вектор приоритетов k-й матрицы суждений, расположенной на третьем уровне;

q_2k – k-й элемент вектор приоритетов матрицы суждений, расположенной на втором уровне;

q_j – приоритет j-го элемента третьего уровня.

Тогда приоритет j-го элемента третьего уровня определяется как:

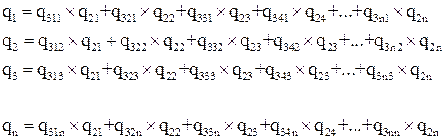(16)

Вопросы для самопроверки:

1. Какими условиями характеризуется среда принятия решений?

2. В чем особенность информационных ограничений процесса принятия решений?

3. Что можно отнести к внешним факторам, оказывающим влияние на процесс принятия решений?

4. Что можно отнести к внутренним факторам, оказывающим влияние на процесс принятия решений?

Литература по теме:

Основная литература:

1. Литвак Б.Г. Управленческие решения: Учебник. – М.: МФПУ «Синергия», 2012. – 512 с. – (Академия бизнеса).

2. Литвак Б.Г. Управленческие решения: Практикум. – М.: МФПУ «Синергия», 2012. – 448 с. – (Академия бизнеса).

Дополнительная литература:

2. Варфоломеев В.И., Воробьев С.Н. Принятие управленческих решений: Учеб пособие для вузов. – М.: КУДИЦ-ОБРАЗ, 2007. – 288 с.

3. Ларичев О.И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах: Учебник. – М.: Логос, 2008. – 392 с.

4. Плис А.И., Сливина Н.А. Mathcad 2000. Математический практикум для экономистов и инженеров: Учеб. пособие. – М.: Финансы и статистика, 2007. – 656 с.

5. Смирнов Э.А. Разработка управленческих решений. – М.: ИНФРА-М., 2008. – 272 с.

6. Трахтенгерц Э.А. Компьютерная поддержка принятия решений: Научно-практическое издание. – М.: СИНТЕГ, 1998. – 376 с.

7. Фатхутдинов Р.А. Разработка управленческого решения: Учеб. пособие. – М.: Бизнес-школа, Интел-Синтез, 2007. – 272 с.

Тема 4. Разработка управленческих решений в условиях неопределенности цели

Цели и задачи:

Цель изучения данной темы – получение общетеоретических знаний о методах принятия решений в условиях неопределенности.

Задачи изучения данной темы:

· рассмотреть общую постановку задачи в условиях неопределенности.

· изучить методы принятия решений в условиях неопределенности.

Вопросы темы:

1. Общая постановка задачи принятия решений в условиях неопределенности.

2. Математические методы принятия решений в условиях неопределенности.

Вопрос 1. Общая постановка задачи принятия решений в условиях неопределенности.

Большинство задач планирования зависит от ряда не известных заранее и неуправляемых факторов. Эти задачи обладают той или иной степенью неопределенности, которая может быть как объективной, так и субъективной, зависящей от индивидуальных психофизических параметров ЛПР. В таких задачах неизвестно распределение вероятностей p(Z_j), с которыми внешняя среда может находиться в одном из возможных состояний . В этом случае ЛПР выдвигает только определенные гипотезы относительно состояний внешней среды.

Таким образом, для ЛПР, действующего в условиях неопределенности и невозможности получения дополнительной информации о неопределенных факторах, элементами описания ситуации планирования являются:

· множество допустимых стратегий (множество возможных альтернатив действий ЛПР)

· множество возможных состояний внешней среды (множество гипотез)

Предполагается, что на множестве отношений АZ можно задать некоторую функцию полезности f(A_i,Z_j), которая выступает в качестве меры желательности или полезности соответствующей альтернативы. Если множества A и Z конечны, то мера для оценки эффективности действий ЛПР (полезность исходов) представима в виде матрицы. Каждое конкретное значение элемента матрицы характеризует выбор i-й стратегии (альтернативы A_i) при состоянии внешней среды Z_j. Для выбора лучшей стратегии имеется ряд специальных методов, ориентированных на использование в условиях неопределенности, которые рассмотрены и проиллюстрированы ниже.

Вопрос 2. Математические методы принятия решений в условиях неопределенности.

Критерий максимина (принцип гарантированного результата, или критерий Вальда).

Данный принцип заключается в выборе в качестве оптимальной (наиболее эффективной) той альтернативы (стратегии), которая имеет наибольшее среди наименее благоприятных состояний внешней среды значение функции полезности. Таким образом, оптимальной, считается альтернатива A*, для которой выполняется соотношение:

(17)

Здесь e_ij есть значение функции полезности при альтернативе и состоянии внешней среды . Найденная оптимальная альтернатива A* выбранная по критерию Вальда, обеспечивает гарантированный выигрыш (успех в достижении цели) при наихудшем для данной фирмы состоянии внешней среды.

Рассмотрим следующий пример. Исходная таблица решений характеризуется данными, приведенными в табл. 9.

Таблица 9.

Ожидаемые значения прибыли (тыс. ден. ед.) для трех товарных рынков

Возможные новые товарные рынки	Политическая обстановка
	стабильная	стабильная	нестабильная	нестабильная
	Степень конкуренции
	слабая, Z₁	сильная, Z₂	слабая, Z₃	сильная, Z₄
Рынок, А₁	530	460	240	220
Рынок, А₂	490	390	300	270
Рынок, А₃	575	420	260	190

Сначала для каждой альтернативы выбираем по соответствующей строке минимальное значение функции полезности, т.е.

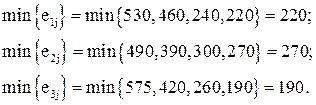
Далее из полученных минимальных значений в соответствии с (17) выбирается максимальное:

Возможные новые товарные рынки	Политическая обстановка						Min по строке
	стабильная	стабильная	нестабильная		нестабильная
	Степень конкуренции
	слабая, Z₁	сильная, Z₂		слабая, Z₃		сильная, Z₄
Рынок, А₁	530	460		240		220	220
Рынок, А₂	490	390		300		270	270 = max
Рынок, А₃	575	420		260		190	190

Следовательно, оптимальной по критерию максимина является альтернатива А₂, т.е. фирме целесообразно выходить со своим товаром на рынок А₂. Это самая осторожная стратегия, так как при любом состоянии внешней среды фирма получит прибыль не менее 270 тыс. ден. ед.

Критерий максимакса (принцип безудержного оптимизма).

Если критерий максимина ориентирован на получение гарантированного минимума желаемого результата (правило «лучший из худших»), то критерий оптимизма предполагает возможность получения максимального уровня желательности результата. Эта альтернатива А* выбирается исходя из выражения

(18)

Рассматривая исходные данные (табл. 8) с точки зрения принципа оптимизма (18), получим:

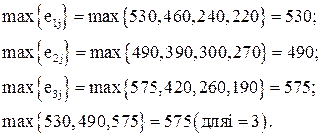
Таким образом, оптимальной по критерию оптимизма будет альтернатива А₃, для которой справедливо соотношение:

Возможные новые товарные рынки	Политическая обстановка				Max по строке
	стабильная	стабильная	нестабильная	нестабильная
	Степень конкуренции
	слабая, Z₁	сильная, Z₂	слабая, Z₃	сильная, Z₄
Рынок, А₁	530	460	240	220	530
Рынок, А₂	490	390	300	270	490
Рынок, А₃	575	420	260	190	575 = max

Критерий Гурвица.

Данный критерий представляет собой комбинацию принципа гарантированного результата и принципа оптимизма. Функция, описывающая критерий Гурвица, представляется в виде:

(19)

где е₁(А) – стратегия выбора альтернативы, характеризующая принцип гарантированного результата, а e₂(A) – принципа оптимизма; – весовой коэффициент.

Так как

то общее выражение для принципа Гурвица на основании (19) будет иметь следующий вид:

или

Здесь используются две гипотезы: суть первой в том, что среда находится с вероятностью в самом невыгодном состоянии, и второй – что среда находится с вероятностью в самом выгодном состоянии.

В зависимости от значения весового коэффициента можно получить различные предпочтительные альтернативы. Причем если , то имеем принцип оптимизма, если , то получим принцип гарантированного результата.

Используя этот критерий, обратимся опять к нашим данным (табл. 9). Пусть весовой коэффициент, характеризующий степень важности соответствующей альтернативы, равен 0,7. Тогда получим:

(20)

Подставляя значения из табл. 8 в выражение (20), имеем:

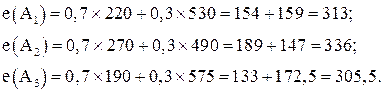
Далее производим выбор на основе следующей стратегии:

Подставляя вычисленные ранее значения, получим:

Таким образом, оптимальной по принципу Гурвица при коэффициенте будет альтернатива A₂.

Приведем решение данным методом в следующей таблице:

Возможные новые рынки	Политическая обстановка				Критерий е(А) по строкам
	стабильная	стабильная	нестабил.	нестабил.
	Степень конкуренции
	слабая,Z₁	сильная,Z₂	слабая,Z₃	сильная,Z₄
Рынок, А₁	530 = max(A₁)	460	240	220 = min(A₁)	0,7 · 220 + 0,3 · 530 = 313
Рынок, А₂	490 = max(A₂)	390	300	270 = min(A₂)	0,7 · 270 + 0,3 · 490 = 336 = max
Рынок, А₃	575 = max(A₃)	420	260	190 =min(A₃)	0,7·190 + 0,3 · 575 = 305,5

Если же весовой коэффициент равен 0,2, то решение изменится следующим образом:

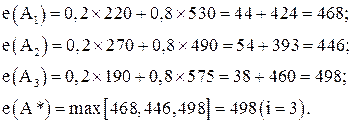
Оптимальной стратегией в этом случае будет работа фирмы на рынке A₃.

Приведем решение в виде таблицы:

Возможные новые рынки	Политическая обстановка				Критерий е(А) по строкам
	стабильная	стабильная	нестабил.	нестабил.
	Степень конкуренции
	слабая,Z₁	сильная,Z₂	слабая,Z₃	сильная,Z₄
Рынок, А₁	530 = max(A₁)	460	240	220 = min(A₁)	0,2 · 220 + 0,8 · 530 = 468
Рынок, А₂	490 = max(A₂)	390	300	270 = min(A₂)	0,2 · 270 + 0,8 · 490 = 446
Рынок, А₃	575 = max(A₃)	420	260	190 = min(A₃)	0,2 · 190 + 0,8 · 575 = 498 = max

Наконец, если положить , то получим следующее решение:

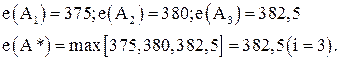
И в этом случае оптимальной стратегией будет работа на рынке A₃.

Приведем решение в виде таблицы:

Возможные новые рынки	Политическая обстановка				Критерий е(А) по строкам
	стабильная	стабильная	нестабил.	нестабил.
	Степень конкуренции
	слабая,Z₁	сильная,Z₂	слабая,Z₃	сильная,Z₄
Рынок, А₁	530 = max(A₁)	460	240	220 = min(A₁)	0,5 · 220 + 0,5 · 530 = 375
Рынок, А₂	490 = max(A₂)	390	300	270 = min(A₂)	0,5 · 270 + 0,5 · 490 = 380
Рынок, А₃	575 = max(A₃)	420	260	190 = min(A₃)	0,5 · 190 + 0,5 · 575 = 382,5 = max

Заметим, что если фирма желает, например, работать на всех трех рынках, то, используя принцип Гурвица, можно принять следующее решение по распределению долей продукции (долей объемов продаж) между рынками, применив формулу:

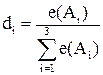где

d_i. – доля товара в натуральном или денежном выражении, реализуемого на рынке A_i, i = 1, 2, 3.

В общем случае процентное соотношение распределения товара по рынкам с использованием критерия Гурвица может быть вычислено по аналогичной формуле:

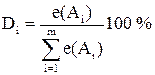(21)

где

D_i – доля товара, реализуемого на рынке A_i, выраженная в процентах;

m – количество рассматриваемых рынков.

В нашем примере при , если рассматривать все три рынка, то, используя формулу (21), получим следующее процентное распределение товара между рынками:

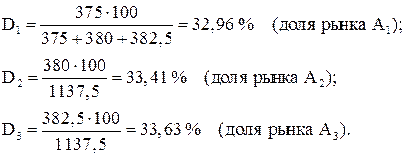
Однако представляется более рациональным распределить товар между рынками A₂ и А₃, так как рынок A₂ должен быть выбран согласно принципу гарантированного результата, а рынок A₃ – согласно принципу оптимизма, причем изменение весового коэффициента в принципе Гурвица приводит к тем же альтернативам A₂ и A₃. Поэтому, используя формулу (21) для двух рынков и , получим следующее процентное распределение товара между ними:

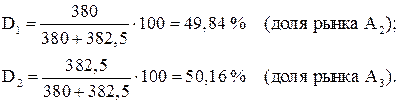
Вообще говоря, здесь мы имеем пропорциональное распределение рисков. Данный подход может быть использован в практических расчетах.

Критерий минимаксного сожаления (принцип Сэвиджа).

Стратегия выбора по принципу Сэвиджа характеризует те потенциальные потери, которые фирма будет иметь, если выберет неоптимальное решение. Детализированная процедура выбора в этом случае производится в три этапа.

1. Для каждого состояния внешней среды по конкретной альтернативе определяется максимальное значение функции полезности:

(22)

Это есть, возможно, наилучший уровень полезности, который можно получить для конкретного состояния внешней среды Z_j.

2. На основании значений, вычисленных по формуле (22), для каждой альтернативы строится показатель:

(23)

Данный показатель характеризует потенциальный риск, а точнее потерянную выгоду от выбора неоптимальной альтернативы. В результате этого действия формируется матрица потенциальных потерь.

3. Используя полученную на предыдущем этапе матрицу потерь (или, как еще говорят, матрицу сожалений), производится выбор стратегии с наименьшим показателем риска:

(24)

Данный критерий минимизирует возможные потери при условии, что состояние внешней среды наихудшим образом отличается от предполагаемого. Рассмотрим применение принципа Сэвиджа на исходных данных (табл. 8) в соответствии с описанной выше процедурой.

1. Для значений функции полезности по каждому состоянию внешней среды Z₁, Z₂, Z₃, Z₄ на основании (22) определим максимальный уровень полезности:

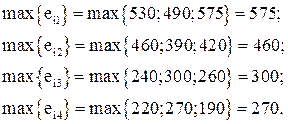
Возможные новые товарные рынки	Политическая обстановка
	стабильная	стабильная	нестабильная	нестабильная
	Степень конкуренции
	слабая, Z₁	сильная, Z₂	слабая, Z₃	сильная, Z₄
Рынок, А₁	530	460 = max(Z2)	240	220
Рынок, А₂	490	390	300 = max(Z3)	270 = max(Z4)
Рынок, А₃	575 = max(Z₁)	420	260	190

2. Вычислим элементы матрицы потенциальных потерь согласно формуле (23):

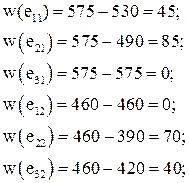
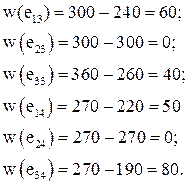
Таким образом, матрица потерь будет иметь следующий вид.

Таблица 10.

Матрица потенциальных потерь

Альтернативы	Состояния внешней среды
Альтернативы	Z₁	Z₂	Z₃	Z₄
А₁	575 – 530 = 45	460 – 460 = 0	300 – 240 = 60	270 – 220 = 50
А₂	575 – 490 = 85	70	0	0
А₃	575 – 575 = 0	40	40	80

3. На основании матрицы потерь (табл. 10) можно определить максимальные потери по каждой альтернативе. Для этого применим правило:

Для каждого I = 1,2,3 определим:

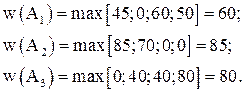
Альтернативы	Состояния внешней среды
Альтернативы	Z₁	Z₂	Z₃	Z₄
А₁	45	0	60 = max(A1) = min(max)	50
А₂	85 = max(A₂)	70	0	0
А₃	0	40	40	80 = max(A3)

Оптимальной будет та альтернатива, которая имеет минимальные потери согласно выражению (14):

т.е.

Следовательно, оптимальна альтернатива A₁ имеющая минимальные потери выгоды.

Критерий Лапласа.

Данный критерий применяется, если состояния внешней среды неизвестны, но их можно считать равновероятными, т.е.

Решающее правило в этом случае имеет следующий вид:

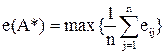В рассматриваемом примере:

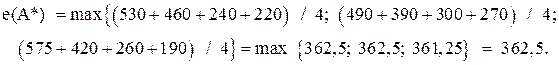
Следовательно, с точки зрения критерия Лапласа можно выбрать как рынок A₁, так и рынок A₂.

	Политическая обстановка				Критерий е(А) по строкам
	стабильная	стаб.	нестаб.	нестаб.
	Степень конкуренции
	слабая,Z₁	сильная,Z₂	слабая,Z₃	сильная,Z₄
А₁	530	460	240	220	(530+460+240+220) / 4 = 362,5 = max
А₂	490	390	300	270	(490 + 390 + 300 + 270) / 4 = 362,5
А₃	575	420	260	190	(575 + 420 + 260 + 190) / 4 = 361,25 = max

Сделаем несколько практических рекомендаций по применению рассмотренных выше критериев (принципов):

1. Критерий Вальда лучше всего использовать тогда, когда фирма желает свести риск от принятого решения к минимуму.

2. Коэффициент в критерии Гурвица выбирается из субъективных соображений: чем опаснее ситуация, тем больше ЛПР желает подстраховаться.

3. Критерий Сэвиджа удобен, если для предприятия приемлем некоторый риск.

4. Критерий Лапласа может быть применен, когда ЛПР не может предпочесть ни одной гипотезы.

Вопросы для самопроверки:

1. В каких экономических условиях используют критерий Вальда?

2. Чем обосновано использование критерия Гурвица?

3. В каких случаях используют критерий Сэвиджа?

4. Что лежит в основе критерия Лапласа?

5. Расчеты какого показателя отличают неопределенность и риск?

Литература по теме:

Основная литература:

1. Литвак Б.Г. Управленческие решения: Учебник. – М.: МФПУ «Синергия», 2012. – 512 с. – (Академия бизнеса).

2. Литвак Б.Г. Управленческие решения: Практикум. – М.: МФПУ «Синергия», 2012. – 448 с. – (Академия бизнеса).

Дополнительная литература:

2. Ашихмин А.А. Разработка и принятие управленческих решений: формальные модели и методы выбора. – М.: МГТУ, 2005.

3. Варфоломеев В.И., Воробьев С.Н. Принятие управленческих решений: Учеб пособие для вузов. – М.: КУДИЦ-ОБРАЗ, 2007. – 288 с.

4. Ларичев О.И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах: Учебник. – М.: Логос, 2008. – 392 с.

5. Плис А.И., Сливина Н.А. Mathcad 2000. Математический практикум для экономистов и инженеров: учеб. пособие. – М.: Финансы и статистика, 2007. – 656 с.

6. Смирнов Э.А. Разработка управленческих решений. – М.: ИНФРА-М, 2008. – 272 с.

7. Трахтенгерц Э.А. Компьютерная поддержка принятия решений: Научно-практическое издание. – М.: СИНТЕГ, 1998. – 376 с.

8. Фатхутдинов Р.А. Разработка управленческого решения: Учеб. пособие. – М.: Бизнес-школа, Интел-Синтез, 2007. – 272 с.

Тема 5. Разработка управленческих решений в условиях риска

Цели и задачи:

Цель изучения данной темы – получение общетеоретических знаний о методах и подходах к процессу принятия решений в условиях риска.

Задачи изучения данной темы:

· изучение содержания понятия «риск» при построении процесса принятия управленческих решений;

· изучение математических методов принятия управленческих решений в условиях риска;

Вопросы темы:

1. Содержание понятия «риск» при принятии управленческих решений.

2. Структура байесовского и небайесовского алгоритмов принятия решения при риске.

3. Дерево решений как инструмент принятия решений.

Вопрос 1. Содержание понятия «риск» при принятии управленческих решений.

Когда выбор планового решения осуществляется в условиях риска, известны или задаются субъективные вероятности возможных состояний внешней среды. При этом постановка задачи будет следующей:

a) имеется множество альтернатив и множество состояний внешней среды

b) известны субъективные вероятности состояния среды причем.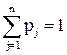

c) для каждого сочетания альтернативного решения A_i и состояния Z_j задана функциональная полезность e_ij.

Существующие методы выбора базируются в основном на использовании вероятностных мер в качестве критериев выбора. В теории статистических решений обычно используются принцип Байеса, принцип Бернулли и принцип энтропии математического ожидания функции полезности.

Базовыми методами риск-менеджмента являются отказ от риска, снижение, передача и принятие. Риск-инструментарий значительно шире. Он включает политические, организационные, правовые, экономические, социальные инструменты, причем риск-менеджмент как система допускает возможность одновременного применения нескольких методов и инструментов риск-управления.

Наиболее часто применяемым инструментом риск-менеджмента является страхование. Страхование предполагает передачу ответственности за возмещение предполагаемого ущерба сторонней организации (страховой компании). Примерами других инструментов могут быть:

· отказ от чрезмерно рисковой деятельности (метод отказа);

· профилактика или диверсификация (метод снижения);

· аутсорсинг затратных рисковых функций (метод передачи);

· формирование резервов или запасов (метод принятия).

Подходы к оцениванию рисков.

Понятие «риск», как уже отмечалось, многогранно. Например, при использовании статистических методов управления качеством продукции риски (точнее, оценки рисков) – это вероятности некоторых событий. В статистическом приемочном контроле «риск поставщика» – это вероятность забракования партии продукции хорошего качества, а «риск потребителя» – приемки «плохой» партии. При статистическом регулировании технологических процессов рассматривают риск незамеченной разладки и риск излишней наладки.

Тогда оценка риска – это оценка вероятности, точечная или интервальная, по статистическим данным или экспертная. В таком случае для управления риском задают ограничения на вероятности нежелательных событий.

Иногда под уменьшением риска понимают уменьшение дисперсии случайной величины, поскольку при этом уменьшается неопределенность. В теории принятия решений риск – это плата за принятие решения, отличного от оптимального, он обычно выражается как математическое ожидание. В экономике плата измеряется обычно в денежных единицах, т.е. в виде финансового потока (потока платежей и поступлений) в условиях неопределенности.

Методы математического моделирования позволяют предложить и изучить разнообразные методы оценки риска. Широко применяются два вида методов – статистические, основанные на использовании эмпирических данных, и экспертные, опирающиеся на мнения и интуицию специалистов.

Вопрос 2. Структура байесовского и небайесовского алгоритмов принятия решения при риске.

Принцип Байеса.

В качестве критерия выбора стратегии (альтернативы) A_i применяются взвешенные по вероятности суммы полезностей, т.е.

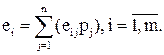(25)

Оптимальным считается решение A*, для которого значение критерия e_i будет максимальным или минимальным в зависимости от постановки задачи:

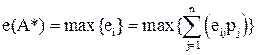(26)

или

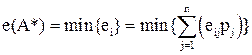
Если в примере (табл. 8) задать вероятности p₁= 0,4; p₂= 0,2; р₃= 0,1; р₄= 0,3, то на основе (25) и (26) получим:

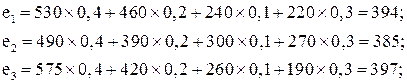
Следовательно, оптимальной является альтернатива A₃.

Новые рынки	Политическая обстановка				Значение критерия е по строкам
	стабильная	стабильная	нестаб.	нестаб.
	Степень конкуренции
	слабая,Z₁	сильная,Z₂	слабая,Z₃	сильная,Z₄
А₁	530	460	240	220	530 · 0,4 + 460 · 0,2 + 240 · 0,1 + 220 · 0,3 = = 394
А₂	490	390	300	270	385
А₃	575	420	260	190	397 = max
Вероятность, p_j	0,4	0,2	0,1	0,3

Иногда каждому решению A₁, ставят в соответствие не значение функции полезности e_ij, а величину потерь w_ij = |e_ij-max{e_ij}|, которая характеризует упущенные возможности. Тогда:

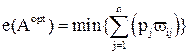(27)

Используя матрицу потенциальных потерь (табл. 10), вычислим с учетом вероятностей наступления тех или иных состояний среды общие потери:

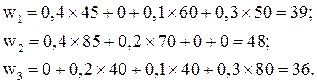
На основе формулы (27) имеем:

Оптимальной альтернативой является A₃.

Альтернативы	Состояния внешней среды				Критерии w по строкам
Альтернативы	Z₁	Z₂	Z₃	Z₄	Критерии w по строкам
А₁	45	0	60	50	45 · 0,4 + 0 · 0,2 + 60 · 0,1 + 50 · 0,3 = 39
А₂	85	70	0	0	48
А₃	0	40	40	80	36 = min
Вероятность, p_j	0,4	0,2	0,1	0,3

Принцип Бернулли.

При использовании данного принципа исходят из того, что известна некоторая функция полезности u(е). Эта субъективная функция полезности Бернулли ставит в соответствие каждому возможному вероятностному значению альтернативы определенную величину полезности. Для каждой альтернативы можно определить ожидаемое значение полезности ее вероятностного результата. Оптимальной считается альтернатива с наибольшим ожидаемым значением полезности, т. е. оптимальной стратегии соответствует

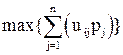Вид функции полезности Бернулли зависит от отношения ЛПР к риску. Принципиальный вид функции полезности:

а) при нейтральном (безразличном) отношении к риску;

б) при существенном учете риска;

в) при малой значимости риска представлен на рис. 3.

Здесь следует заметить, что на различных интервалах изменения аргумента функция полезности может иметь различный вид с точки зрения отношения к риску.

Рассмотрим принцип Бернулли применительно к задаче, исходные данные которой представлены в табл. 9, а вероятности состояния внешней среды такие же, как и в примере, иллюстрирующем принцип Байеса, а именно р₁= 0.4; p₂= 0,2; p₃= 0,1; р₄= 0,3.

В результате проведенных расчетов функция полезности Бернулли имеет следующий вид:

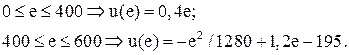
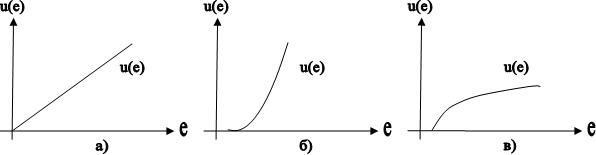
Рис. 3. Вид функции полезности Бернулли при различных точках зрения на риск

График данной функции изображен на рис. 4. Результаты определения оптимальной альтернативы (нового целевого рынка) по принципу Бернулли помещены в табл. 11.

Таблица 11.

Значения функции полезности Бернулли

Альтернативы	Состояния внешней среды				Ожидаемые значения полезности
Альтернативы	Z₁	Z₂	Z₃	Z₄	Ожидаемые значения полезности
A₁	222	192	96	88	163,2
A₂	205	156	120	108	157,6
A₃	237	171	104	76	162,2 = max(A)
Вероятность, *p_j*	0,4	0,2	0,1	0,3

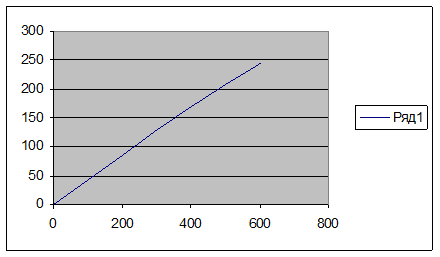
Рис. 4. Функция полезности Бернулли u(е)

Согласно принципу Бернулли, оптимальной стратегией будет A₁.

Замечание. Рассмотренные выше методы представляют собой индивидуальный выбор альтернатив, т.е. когда решение принимает одно лицо или несколько лиц, имеющих единое мнение. Однако могут быть применены и методы группового выбора.

Вопрос 3. Дерево решений как инструмент принятия решений.

Своевременная разработка и принятие правильного решения – главные задачи работы управленческого персонала любой организации. Непродуманное решение может дорого стоить компании. На практике результат одного решения заставляет нас принимать следующее решение и т.д. Когда нужно принять несколько решений в условиях неопределенности, когда каждое решение зависит от исхода предыдущего решения или исходов испытаний, то применяют схему, называемую деревом решений.

Дерево решений, как уже было сказано выше, – это графическое изображение процесса принятия решений, в котором отражены альтернативные решения, альтернативные состояния среды, соответствующие вероятности, и выигрыши для любых комбинаций альтернатив и состояний среды.

Рисуют деревья слева направо. Места, где принимаются решения, обозначают квадратами □, места появления исходов – кругами ○, возможные решения – пунктирными линиями --------, возможные исходы – сплошными линиями ––––.

Для каждой альтернативы мы считаем ожидаемую стоимостную оценку (EMV) – максимальную из сумм оценок выигрышей, умноженных на вероятность реализации выигрышей, для всех возможных вариантов.

Пример 1. (по материалам сайта «Экономика и финансы»).

Главному инженеру компании надо решить, монтировать или нет новую производственную линию, использующую новейшую технологию. Если новая линия будет работать безотказно, компания получит прибыль 200 млн. рублей. Если же она откажет, компания может потерять 150 млн рублей. По оценкам главного инженера, существует 60 %-ная вероятность того, что новая производственная линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет производственную линию. Эксперимент обойдется в 10 млн рублей. Главный инженер считает, что существует 50 %-ная вероятность того, что экспериментальная установка будет работать. Если экспериментальная установка будет работать, то 90 % – за то, что смонтированная производственная линия также будет работать. Если же экспериментальная установка не будет работать, то только 20 % – за то, что производственная линия заработает. Следует ли строить экспериментальную установку? Следует ли монтировать производственную линию? Какова ожидаемая стоимостная оценка наилучшего решения?

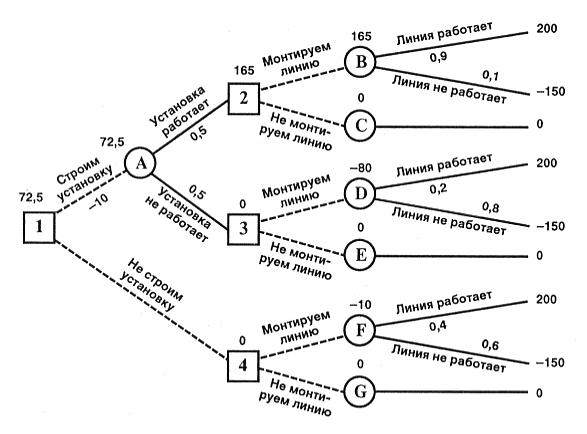
Рис. 5. Дерево решений

В узле F возможны исходы «линия работает» с вероятностью 0,4 (что приносит прибыль 200) и «линия не работает» с вероятностью 0,6 (что приносит убыток -150) => оценка узла F.. Это число мы пишем над узлом F.

В узле 4 мы выбираем между решением «монтируем линию» (оценка этого решения EMV(F) = -10) и решением «не монтируем линию» (оценка этого решения. Эту оценку мы пишем над узлом 4, а решение «монтируем линию» отбрасываем и зачеркиваем.

Аналогично:

. Поэтому в узле 2 отбрасываем возможное решение «не монтируем линию».

. Поэтому в узле 3 отбрасываем возможное решение «монтируем линию».

. Поэтому в узле 1 отбрасываем возможное решение «не строим установку».

Ожидаемая стоимостная оценка наилучшего решения равна 72,5 млн. рублей. Строим установку. Если установка работает, то монтируем линию. Если установка не работает, то линию монтировать не надо.

Пример 2 (по материалам сайта «Экономика и финансы»).

Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий.

A. Построить большой завод стоимостью M₁ = 700 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере R₁ = 280 тысяч долларов в течение следующих 5 лет) с вероятностью p₁ = 0,8 и низкий спрос (ежегодные убытки R₂ = 80 тысяч долларов) с вероятностью р₂ = 0,2.

B. Построить маленький завод стоимостью М₂ = 300 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере T₁= 180 тысяч долларов в течение следующих 5 лет) с вероятностью p₁= 0,8 и низкий спрос (ежегодные убытки Т₂ = 55 тысяч долларов) с вероятностью р₂ = 0,2.

C. Отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью p₃ = 0,7 и p₄ = 0,3 соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, а вероятности большого и низкого спроса меняются на p₅ = 0,9 и р₆ = 0,1 соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет.

Все расчеты выражены в текущих ценах и не должны дисконтироваться. Нарисовав дерево решений, определим наиболее эффективную последовательность действий, основываясь на ожидаемых доходах.

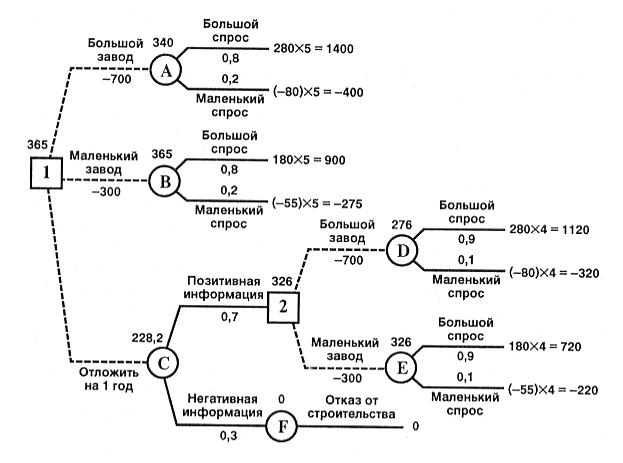
Рис. 6. Дерево решений

Ожидаемая стоимостная оценка узла А равна

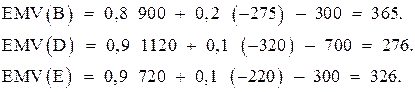
. Поэтому в узле 2 отбрасываем возможное решение «большой завод».

. Поэтому в узле 1 выбираем решение «маленький завод». Исследование проводить не нужно. Строим маленький завод. Ожидаемая стоимостная оценка этого наилучшего решения равна 365 тысяч долларов.

Литература по теме:

Основная литература:

1. Литвак Б.Г. Управленческие решения: Учебник. – М.: МФПУ «Синергия», 2012. – 512 с. – (Академия бизнеса).

2. Литвак Б.Г. Управленческие решения: Практикум. – М.: МФПУ «Синергия», 2012. – 448 с. – (Академия бизнеса).

Дополнительная литература:

2. Ашихмин А.А. Разработка и принятие управленческих решений: формальные модели и методы выбора. – М.: МГТУ, 2005.

5. Плис А.И., Сливина Н.А. Mathcad 2000. Математический практикум для экономистов и инженеров: Учеб. пособие. – М.: Финансы и статистика, 2007. – 656 с.

6. Смирнов Э.А. Разработка управленческих решений. – М.: ИНФРА-М, 2008. – 272 с.

Тема 6. Разработка управленческих решений в условиях конфликта и коллективом экспертов

Цели и задачи:

Цель изучения данной темы – получение общетеоретических знаний о теории игр и методе экспертных оценок.

Задачи изучения данной темы:

· изучение классификации игр;

· изучение особенностей решения матричных игр в чистых стратегиях;

· изучение смешанных стратегий в матричных играх;

· изучение критериев принятия решений в статистических играх.

Вопросы темы:

1. Решение матричных игр в чистых стратегиях.

2. Смешанные стратегии в матричных играх.

3. Принятие решений в условиях неопределенности.

4. Метод экспертных оценок.

Вопрос 1. Решение матричных игр в чистых стратегиях.

Игра (в математике) – это идеализированная математическая модель коллективного поведения: несколько игроков влияют на исход игры, причем их интересы различны [доп. 3].

Регулярное действие, выполняемое игроком во время игры, называется ходом. Совокупность ходов игрока, совершаемых им для достижения цели игры, называется стратегией.

Классификация игр.

Классификацию игр можно проводить: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т.д.

В зависимости от количества игроков различают игры двух и n игроков. Первые из них наиболее изучены. Игры трех и более игроков менее исследованы из-за возникающих принципиальных трудностей и технических возможностей получения решения.

По количеству стратегий игры делятся на конечные и бесконечные. Если в игре все игроки имеют конечное число возможных стратегий, то она называется конечной. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий, игра называется бесконечной.

По характеру взаимодействия игры делятся на бескоалиционные, когда игроки не имеют права вступать в соглашения, образовывать коалиции, и коалиционные (кооперативные), когда игроки могут вступать в коалиции.

В кооперативных играх коалиции заранее определены.

По характеру выигрышей игры делятся на игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой.

По виду функций выигрыша игры делятся на матричные, биматричные, непрерывные, выпуклые и др.

Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задается выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 1, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям).

Для матричных игр доказано, что любая из них имеет решение, и оно может быть легко найдено путем сведения игры к задаче линейного программирования.

Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2).

Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной. Доказано, что игры этого класса имеют решения, однако не разработано практически приемлемых методов их нахождения.

Если функция выигрышей является выпуклой, то такая игра называется выпуклой. Для них разработаны приемлемые методы решения, состоящие в отыскании чистой оптимальной стратегии (определенного числа) для одного игрока и вероятностей применения чистых оптимальных стратегий другого игрока. Такая задача решается сравнительно легко.

Запись матричной игры в виде платежной матрицы.

В общем виде матричная игра может быть записана следующей платежной матрицей [1, 2, доп. 3] (рис. 7).

	B1	B2	…	Bn
A1	A₁₁	A₁₂	...	A_1n
A2	A₂₁	A₂₂	...	A_2n
…	...	...	...	...
Am	a_m1	a_m2	...	a_mn

Рис. 7. Общий вид платежной матрицы матричной игры

где

A_i – названия стратегий игрока 1;

B_j – названия стратегий игрока 2;

a_ij – значения выигрышей игрока 1 при выборе им i-й стратегии, а игроком 2 – j-й стратегии.

Поскольку данная игра является игрой с нулевой суммой, значение выигрыша для игрока 2 является величиной, противоположенной по знаку значению выигрыша игрока 1.

Понятие о нижней и верхней цене игры. Решение игры в чистых стратегиях.

Каждый из игроков стремится максимизировать свой выигрыш с учетом поведения противодействующего ему игрока. Поэтому для игрока 1 необходимо определить минимальные значения выигрышей в каждой из стратегий, а затем найти максимум из этих значений, то есть определить величину

или найти минимальные значения по каждой из строк платежной матрицы, а затем определить максимальное из этих значений. Величина называется максимином матрицы, или нижней ценой игры.

Величина выигрыша игрока 1 равна, по определению матричной игры, величине проигрыша игрока 2. Поэтому для игрока 2 необходимо определить значение

или найти максимальные значения по каждому из столбцов платежной матрицы, а затем определить минимальное из этих значений. Величина называется минимаксом матрицы, или верхней ценой игры.

В случае если значения и не совпадают, при сохранении правил игры (коэффициентов ) в длительной перспективе выбор стратегий каждым из игроков оказывается неустойчивым. Устойчивость он приобретает лишь при равенстве . В этом случае говорят, что игра имеет решение в чистых стратегиях, а стратегии, в которых достигается – оптимальными чистыми стратегиями. Величина называется чистой ценой игры [доп. 4].

Например, в матрице (рис. 8) существует решение в чистых стратегиях. При этом для игрока 1 оптимальной чистой стратегией будет стратегия A1, а для игрока 2 – стратегия B4.

	B1	B2	B3	B4	Min_j
A1	7	6	5	4	4
A2	1	8	2	3	1
A3	8	1	3	2	1
Max_i	8	8	5	4

Рис. 8. Платежная матрица, в которой существует решение в чистых стратегиях

В матрице (рис. 9) решения в чистых стратегиях не существует, так как нижняя цена игры достигается в стратегии A1 и ее значение равно 2, в то время как верхняя цена игры достигается в стратегии B4 и ее значение равно 3.

	B1	B2	B3	B4	Min_j
A1	7	6	5	2	2
A2	1	8	2	3	1
A3	8	1	3	2	1
Max_i	8	8	5	3

Рис. 9. Платежная матрица, в которой не существует решения в чистых стратегиях

Уменьшение порядка платежной матрицы.

Порядок платежной матрицы (количество строк и столбцов) может быть уменьшен за счет исключения доминируемых и дублирующих стратегий.

Стратегия K* называется доминируемой стратегией K**, если при любом варианте поведения противодействующего игрока выполняется соотношение:

где

A_k_* и A_k_** – значения выигрышей при выборе игроком, соответственно, стратегий K* и K**.

В случае если выполняется соотношение

стратегия K* называется дублирующей по отношению к стратегии K**.

Например, в матрице (рис. 10) стратегия A1 является доминируемой по отношению к стратегии A2, стратегия B6 является доминируемой по отношению к стратегиям B3, B4 и B5, а стратегия B5 является дублирующей по отношению к стратегии B4. Данные стратегии не будут выбраны игроками, так как являются заведомо проигрышными и удаление этих стратегий из платежной матрицы не повлияет на определение нижней и верхней цены игры, описанной данной матрицей.

	B1	B2	B3	B4	B5	B6
A1	1	2	3	4	4	7
A2	7	6	5	4	4	8
A3	1	8	2	3	3	6
A4	8	1	3	2	2	5

Рис. 10. Платежная матрица с доминируемыми и дублирующими стратегиями

Множество недоминируемых стратегий, полученных после уменьшения размерности платежной матрицы, называется еще множеством Парето (по имени итальянского экономиста Вильфредо Парето, занимавшегося исследованиями в данной области).

Пример решения матричной игры в чистых стратегиях.

Рассмотрим пример решения матричной игры в чистых стратегиях, в условиях реальной экономики, в ситуации борьбы двух предприятий за рынок продукции региона.

Задача.

Два предприятия производят продукцию и поставляют ее на рынок региона. Они являются единственными поставщиками продукции в регион, поэтому полностью определяют рынок данной продукции в регионе.

Каждое из предприятий имеет возможность производить продукцию с применением одной из трех различных технологий. В зависимости от качества продукции, произведенной по каждой технологии, предприятия могут установить цену единицы продукции на уровне 10, 6 и 2 денежных единиц соответственно. При этом предприятия имеют различные затраты на производство единицы продукции.

Таблица 12.

Затраты на единицу продукции, произведенной на предприятиях региона (д.е.)

Технология	Цена реализации единицы продукции, д.е.	Полная себестоимость единицы продукции, д.е.
Технология	Цена реализации единицы продукции, д.е.	Предприятие 1	Предприятие 2
I	10	5	8
II	6	3	4
III	2	1.5	1

В результате маркетингового исследования рынка продукции региона была определена функция спроса на продукцию:

где

Y – количество продукции, которое приобретет население региона (тыс. ед.), а X – средняя цена продукции предприятий, д.е.

Данные о спросе на продукцию в зависимости от цен реализации приведены в табл. 13.

Таблица 13.

Спрос на продукцию в регионе, тыс. ед.

Цена реализации 1 ед. продукции, д.е.		Средняя цена реализации 1 ед. продукции, д.е.	Спрос на продукцию, тыс. ед.
Предприятие 1	Предприятие 2	Средняя цена реализации 1 ед. продукции, д.е.	Спрос на продукцию, тыс. ед.
10	10	10	1
10	6	8	2
10	2	6	3
6	10	8	2
6	6	6	3
6	2	4	4
2	10	6	3
2	6	4	4
2	2	2	5

Значения долей продукции предприятия 1, приобретенной населением, зависят от соотношения цен на продукцию предприятия 1 и предприятия 2. В результате маркетингового исследования эта зависимость установлена и значения вычислены.

Таблица 14.

Доля продукции предприятия 1, приобретаемой населением в зависимости от соотношения цен на продукцию

Цена реализации 1 ед. продукции, д.е.		Доля продукции предприятия 1, купленной населением
Предприятие 1	Предприятие 2	Доля продукции предприятия 1, купленной населением
10	10	0,31
10	6	0,33
10	2	0,18
6	10	0,7
6	6	0,3
6	2	0,2
2	10	0,92
2	6	0,85
2	2	0,72

По условию задачи, на рынке региона действует только два предприятия. Поэтому долю продукции второго предприятия, приобретенной населением, в зависимости от соотношения цен на продукцию можно определить как «единица минус доля первого предприятия».

Стратегиями предприятий в данной задаче являются их решения относительно технологий производства продукции. Эти решения определяют себестоимость и цену реализации единицы продукции. В задаче необходимо определить:

1. Существует ли в данной задаче ситуация равновесия при выборе технологий производства продукции обоими предприятиями?

2. Существуют ли технологии, которые предприятия заведомо не будут выбирать вследствие невыгодности?

3. Сколько продукции будет реализовано в ситуации равновесия? Какое предприятие окажется в выигрышном положении?

Решение задачи.

1. Определим экономический смысл коэффициентов выигрышей в платежной матрице задачи. Каждое предприятие стремится к максимизации прибыли от производства продукции. Но, кроме того, в данном случае предприятия ведут борьбу за рынок продукции в регионе. При этом выигрыш одного предприятия означает проигрыш другого. Такая задача может быть сведена к матричной игре с нулевой суммой. При этом коэффициентами выигрышей будут значения разницы прибыли предприятия 1 и предприятия 2 от производства продукции. В случае если эта разница положительна, выигрывает предприятие 1, а в случае если она отрицательна – предприятие 2.

2. Рассчитаем коэффициенты выигрышей платежной матрицы. Для этого необходимо определить значения прибыли предприятия 1 и предприятия 2 от производства продукции. Прибыль предприятия в данной задаче зависит:

· от цены и себестоимости продукции;

· от количества продукции, приобретаемой населением региона;

· от доли продукции, приобретенной населением у предприятия.

Таким образом, значения разницы прибыли предприятий, соответствующие коэффициентам платежной матрицы, необходимо определить по формуле (28):

(28)

где

D – значение разницы прибыли от производства продукции предприятия 1 и предприятия 2;

p – доля продукции предприятия 1, приобретаемой населением региона;

S – количество продукции, приобретаемой населением региона;

и – цены реализации единицы продукции предприятиями 1 и 2;

и – полная себестоимость единицы продукции, произведенной на предприятиях 1 и 2.

Вычислим один из коэффициентов платежной матрицы.

Пусть, например, предприятие 1 принимает решение о производстве продукции в соответствии с технологией III, а предприятие 2 – в соответствии с технологией II. Тогда цена реализации единицы продукции для предприятия 1 составит 2 д.е. при себестоимости единицы продукции 1,5 д.е. Для предприятия 2 цена реализации единицы продукции составит 6 д.е. при себестоимости 4 д.е. (табл. 12).

Количество продукции, которое население региона приобретет при средней цене 4 д.е., равно 4 тыс. ед. (табл. 13). Доля продукции, которую население приобретет у предприятия 1, составит 0,85, а у предприятия 2 – 0,15 (табл. 14). Вычислим коэффициент платежной матрицы a₃₂ по формуле (28):

где i = 3 – номер технологии первого предприятия, а j = 2 – номер технологии второго предприятия.

Аналогично вычислим все коэффициенты платежной матрицы. В платежной матрице стратегии – – представляют собой решения о технологиях производства продукции предприятием 1, стратегии – – решения о технологиях производства продукции предприятием 2, коэффициенты выигрышей – разницу прибыли предприятия 1 и предприятия 2.

	B1	B2	B3	Min_j
A1	0,17	0,62	0,24	0,17
A2	3	-1,5	-0,8	-1,5
A3	0,9	0,5	0,4	0,4
Max_i	3	0,62	0,4

Рис. 11. Платежная матрица в игре «Борьба двух предприятий за рынок продукции региона»

В данной матрице нет ни доминируемых, ни дублирующих стратегий. Это значит, что для обоих предприятий нет заведомо невыгодных технологий производства продукции. Определим минимальные элементы строк матрицы. Для предприятия 1 каждый из этих элементов имеет значение минимально гарантированного выигрыша при выборе соответствующей стратегии. Минимальные элементы матрицы по строкам имеют значения: 0,17, -1,5, 0,4.

Определим максимальные элементы столбцов матрицы. Для предприятия 2 каждый из этих элементов также имеет значение минимально гарантированного выигрыша при выборе соответствующей стратегии. Максимальные элементы матрицы по столбцам имеют значения: 3, 0,62, 0,4.

Нижняя цена игры в матрице равна 0,4. Верхняя цена игры также равна 0,4. Таким образом, нижняя и верхняя цена игры в матрице совпадают. Это значит, что имеется технология производства продукции, которая является оптимальной для обоих предприятий в условиях данной задачи. Эта технология III, которая соответствует стратегиям предприятия 1 и предприятия 2. Стратегии и – чистые оптимальные стратегии в данной задаче.

Значение разницы прибыли предприятия 1 и предприятия 2 при выборе чистой оптимальной стратегии положительно. Это означает, что предприятие 1 выиграет в данной игре. Выигрыш предприятия 1 составит 0,4 тыс. д.е. При этом на рынке будет реализовано 5 тыс. ед. продукции (реализация равна спросу на продукцию, табл. 13). Оба предприятия установят цену за единицу продукции в 2 д.е. При этом для первого предприятия полная себестоимость единицы продукции составит 1,5 д.е., а для второго – 1 д.е. (табл. 12). Предприятие 1 окажется в выигрыше лишь за счет высокой доли продукции, которую приобретет у него население.

Вопрос 2. Смешанные стратегии в матричных играх.

Понятие о матричных играх со смешанным расширением.

Исследование в матричных играх начинается с нахождения ее чистой цены. Если матричная игра имеет решение в чистых стратегиях, то нахождением чистой цены заканчивается исследование игры. Если же в игре нет решения в чистых стратегиях, то можно найти нижнюю и верхнюю цены этой игры, которые указывают, что игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры. Улучшение решений матричных игр следует искать в использовании секретности применения чистых стратегий и возможности многократного повторения игр в виде партии. Этот результат достигается путем применения чистых стратегий случайно, с определенной вероятностью.

Смешанной стратегией игрока называется полный набор чистых стратегий, примененных в соответствии с установленным распределением вероятностей. Матричная игра, решаемая с использованием смешанных стратегий, называется игрой со смешанным расширением.

Стратегии, примененные с вероятностью, отличной от нуля, называются активными стратегиями.

Доказано [1, 2, 4, доп. 3, 4, 7], что для всех игр со смешанным расширением существует оптимальная смешанная стратегия, значение выигрыша при выборе которой находится в интервале между нижней и верхней ценой игры:

При этом условии величина V называется ценой игры.

Кроме того, доказано, что если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры V независимо от того, каких стратегий придерживается другой игрок, если только он не выходит за пределы своих активных стратегий. Поэтому для достижения наибольшего гарантированного выигрыша второму игроку также необходимо придерживаться своей оптимальной смешанной стратегии.

Решение матричных игр со смешанным расширением методами линейного программирования.

Решение матричной игры со смешанным расширением – это определение оптимальных смешанных стратегий, то есть нахождение таких значений вероятностей выбора чистых стратегий для обоих игроков, при которых они достигают наибольшего выигрыша.

Для матричной игры, платежная матрица которой показана на рис. 11, V_н ¹ V_в, определим такие значения вероятностей выбора стратегий для игрока 1 (p₁, p₂, …, p_m) и для игрока 2 (q₁, q₂, …, q_n), при которых игроки достигали бы своего максимально гарантированного выигрыша.

Если один из игроков придерживается своей оптимальной стратегии, то по условию задачи его выигрыш не может быть меньше цены игры V. Поэтому данная задача может быть представлена для игроков в виде следующих систем линейных неравенств.

Для первого игрока:

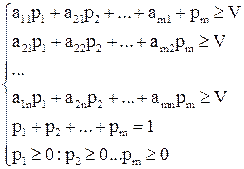
Для второго игрока:

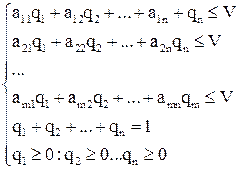
Чтобы определить значение V, разделим обе части каждого из уравнений на V. Величину p_i/V обозначим через x_i, а q_j/V – через y_j.

Для игрока 1 получим следующую систему неравенств, из которой найдем значение 1/v:

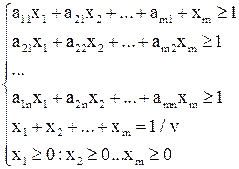
Для игрока 1 необходимо найти максимальную цену игры (V). Следовательно, значение 1/V должно стремиться к минимуму.

Целевая функция задачи будет иметь следующий вид:

Для игрока 2 получим следующую систему неравенств, из которой найдем значение 1/v:

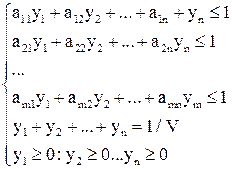
Для игрока 2 необходимо найти минимальную цену игры (V). Следовательно, значение 1/V должно стремиться к максимуму.

Целевая функция задачи будет иметь следующий вид:

Все переменные в данных системах линейных неравенств должны быть неотрицательными:. Значения p_i и q_j не могут быть отрицательными, так как являются значениями вероятностей выбора стратегий игроков. Поэтому необходимо, чтобы значение цены игры V не было отрицательным. Цена игры вычисляется на основе коэффициентов выигрышей платежной матрицы. Поэтому, для того чтобы гарантировать условие неотрицательности для всех переменных, необходимо, чтобы все коэффициенты матрицы были неотрицательными. Этого можно добиться, прибавив перед началом решения задачи к каждому коэффициенту матрицы число K, соответствующее модулю наименьшего отрицательного коэффициента матрицы. Тогда в ходе решения задачи будет определена не цена игры, а величина

Для решения задач линейного программирования используется симплекс-метод. [1, доп. 1].

В результате решения определяются значения целевых функций (для обоих игроков эти значения совпадают), а также значения переменных x_i и y_j.

Величина V* определяется по формуле:

Значения вероятностей выбора стратегий определяются:

· для игрока 1:

· для игрока 2:

Для определения цены игры V из величины V* необходимо вычесть число K.

Пример решения матричной игры со смешанным расширением.

Рассмотрим пример решения матричной игры со смешанным расширением. Платежную матрицу игры составим на основе исходных данных задачи, решенной при выполнении занятия 3, заменив лишь значения долей продукции предприятия 1, приобретаемой населением в зависимости от соотношений цен (табл. 15).

Таблица 15.

Доля продукции предприятия 1, приобретаемой населением в зависимости от соотношения цен на продукцию

Цена реализации 1 ед. продукции, д.е.		Доля продукции предприятия 1, купленной населением
Предп. 1	Предп. 2	Доля продукции предприятия 1, купленной населением
10	10	0,31
10	6	0,33
10	2	0,18
6	10	0,7
6	6	0,3
6	2	0,2
2	10	0,9
2	6	0,85
2	2	0,69

Применив к исходным данным задачи формулу (28) определения разницы прибыли от производства продукции, получим следующую платежную матрицу (рис. 5):

	B1	B2	B3	min_j
A1	0,17	0,62	0,24	0.17
A2	3	-1,5	-0,8	-1.5
A3	0,75	0,5	0,175	0,175
max_i	3	0.62	0.24

Рис. 12. Платежная матрица в игре «Борьба двух предприятий за рынок продукции региона»

В данной матрице (рис. 12) нет доминируемых или дублирующих стратегий. Нижняя цена игры равна 0,175, а верхняя цена игры равна 0,24. Нижняя цена игры не равна верхней. Поэтому решения в чистых стратегиях не существует и для каждого из игроков необходимо найти оптимальную смешанную стратегию.

Решение задачи.

1. В данной матрице имеются отрицательные коэффициенты. Для соблюдения условия неотрицательности в задачах линейного программирования прибавим к каждому коэффициенту матрицы модуль минимального отрицательного коэффициента. В данной задаче к каждому коэффициенту матрицы необходимо прибавить число 1,5 – значение модуля наименьшего отрицательного элемента матрицы. Получим платежную матрицу, преобразованную для выполнения условия не отрицательности (рис. 13)

	B1	B2	B3
A1	1,67	2,12	1,74
A2	4,5	0	0,7
A3	2,25	2	1,675

Рис. 13. Платежная матрица, преобразованная для выполнения условия неотрицательности

2. Опишем задачу линейного программирования для каждого игрока в виде системы линейных неравенств:

Для игрока 1:

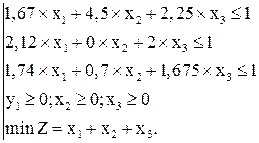
Для игрока 2:

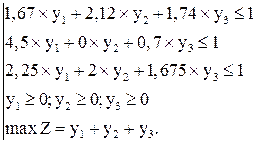
3. Решим обе задачи с использованием симплекс-метода, применяя программный комплекс «Линейная оптимизация».

В результате решения задачи получим следующие значения целевой функции и переменных:

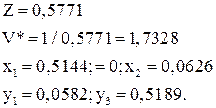
4. Для определения значений вероятностей выбора стратегий игроков 1 и 2 умножим значения переменных на V*.

5. Определим значение цены игры. Для этого из величины V* вычтем 1,5 (значение модуля наименьшего отрицательного элемента).

Таким образом, в данной игре выиграет предприятие 1 (значение V > 0). Для достижения своей оптимальной стратегии (получения максимального математического ожидания гарантированного выигрыша) предприятие 1 должно выбирать технологию 1 с вероятностью 0,8914, а технологию 3 – с вероятностью 0,1083. Предприятие 2, соответственно, должно выбирать технологию 1 с вероятностью 0,1008, а технологию 3 – с вероятностью 0,8991. Значение математического ожидания выигрыша предприятия 1 составит 0,2328 тыс. д.е.

Вопрос 3. Принятие решений в условиях неопределенности.

Понятие о статистических играх.

Принятие управленческих решений предполагает наличие ситуаций выбора наиболее выгодного варианта поведения из нескольких имеющихся вариантов в условиях неопределенности. Такие задачи могут быть описаны матричными играми особого типа, в которых игрок взаимодействует не со вторым игроком, а с окружающей средой. Объективно окружающая среда не заинтересована в проигрыше игрока. В процессе принятия решения о выборе варианта поведения игрок имеет информацию о том, что окружающая среда может принять одно из нескольких возможных состояний и сталкивается с неопределенностью относительно того конкретного состояния, которое примет окружающая среда в данный момент времени.

Матричная игра, в которой игрок взаимодействует с окружающей средой, не заинтересованной в его проигрыше, и решает задачу определения наиболее выгодного варианта поведения с учетом неопределенности состояния окружающей среды, называется статистической игрой или «игрой с природой». Игрок в этой игре называется лицом, принимающим решение (ЛПР). [3, доп. 2, 5, 6].

В общем виде платежная матрица статистической игры приведена на рис. 14.

	S1	S2	…	Sn
A1	A₁₁	A₁₂	...	A₁_n
A2	A₂₁	A₂₂	...	A_2n
…	...	...	...	...
An	a_m1	a_m2	...	a_mn

Рис. 14. Общий вид платежной матрицы статистической игры

В данной игре строки матрицы (A_i) – стратегии ЛПР, а столбцы матрицы (S_j) – состояния окружающей среды.

Критерии принятия решения.

ЛПР определяет наиболее выгодную стратегию в зависимости от целевой установки, которую он реализует в процессе решения задачи. Результат решения задачи ЛПР определяет по одному из критериев принятия решения. Для того чтобы прийти к однозначному и по возможности наиболее выгодному варианту решения, необходимо ввести оценочную (целевую) функцию. При этом каждой стратегии ЛПР (A_i) приписывается некоторый результат W_i, характеризующий все последствия этого решения. Из массива результатов принятия решений ЛПР выбирает элемент W, который наилучшим образом отражает мотивацию его поведения.

Критерий максимального математического ожидания выигрыша.

Критерий максимального математического ожидания выигрыша применяется в тех случаях, когда ЛПР известны вероятности состояний окружающей среды. Платежная матрица дополняется столбцом, каждый элемент которого представляет собой значение математического ожидания выигрыша при выборе соответствующей стратегии ЛПР:

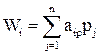, (29)

где

p_j – вероятность j-го состояния окружающей среды.

Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой значение математического ожидания выигрыша максимально:

Применение критерия максимального математического ожидания выигрыша, таким образом, оправдано, если ситуация, в которой принимается решение, следующая:

1. ЛПР известны вероятности всех состояний окружающей среды.

2. Минимизация риска проигрыша представляется ЛПР менее существенным фактором принятия решения, чем максимизация среднего выигрыша.

Необходимость иметь информацию о вероятностях состояний окружающей среды ограничивает область применения данного критерия.

Критерий недостаточного основания Лапласа.

Данный критерий используется при наличии неполной информации о вероятностях состояний окружающей среды в задаче принятия решения. Вероятности состояний окружающей среды принимаются равными, и по каждой стратегии ЛПР в платежной матрице определяется, таким образом, среднее значение выигрыша:

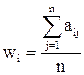(30)

Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой значение среднего выигрыша максимально:

Использование данного критерия оправдано в следующей ситуации:

1. ЛПР не имеет информации либо имеет неполную информацию о вероятностях состояний окружающей среды.

2. Вероятности состояний окружающей среды близки по своим значениям.

3. Минимизация риска проигрыша представляется ЛПР менее существенным фактором принятия решения, чем максимизация среднего выигрыша.

Максиминный критерий Вальда.

Правило выбора решения в соответствии с максиминным критерием (ММ-критерием) можно интерпретировать следующим образом.

Платежная матрица дополняется столбцом, каждый элемент которого представляет собой минимальное значение выигрыша в соответствующей стратегии ЛПР:

(31)

Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой минимальное значение выигрыша максимально:

Выбранная таким образом стратегия полностью исключает риск. Это означает, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Это свойство позволяет считать ММ-критерий одним из фундаментальных.

Применение ММ-критерия оправдано, если ситуация, в которой принимается решение, следующая:

1. О возможности появления состояний окружающей среды ничего не известно.

2. Решение реализуется только один раз.

3. Необходимо исключить какой бы то ни было риск.

Критерий минимаксного риска Сэвиджа

Величина (a_maxj – a_ij), где a_maxj– максимальный элемент j-го столбца, может быть интерпретирована как дополнительный выигрыш, получаемый в условиях состояния окружающей среды S_j при выборе ЛПР наиболее выгодной стратегии, по сравнению с выигрышем, получаемым ЛПР при выборе в тех же условиях любой другой стратегии. Эта же разность может быть интерпретирована как величина возможного проигрыша при выборе ЛПР I-й стратегии по сравнению с наиболее выгодной стратегией. На основе данной интерпретации разности выигрышей производится определение наиболее выгодной стратегии по критерию минимаксного риска.

Для определения оптимальной стратегии по данному критерию на основе платежной матрицы рассчитывается матрица рисков, каждый коэффициент которой (r_ij) определяется по формуле:

(32)

Матрица рисков дополняется столбцом, содержащим максимальные значения коэффициентов r_ij по каждой из стратегий ЛПР:

Оптимальной по данному критерию считается та стратегия, в которой значение R_i минимально:

Ситуация, в которой оправдано применение критерия Сэвиджа, аналогична ситуации ММ-критерия, однако наиболее существенным в данном случае является учет степени воздействия фактора риска на величину выигрыша.

Критерий пессимизма-оптимизма Гурвица.

В практике принятия решений ЛПР руководствуется не только критериями, связанными с крайним пессимизмом или учетом максимального риска. Стараясь занять наиболее уравновешенную позицию, ЛПР может ввести оценочный коэффициент, называемый коэффициентом пессимизма, который находится в интервале [0, 1] и отражает ситуацию, промежуточную между точкой зрения крайнего оптимизма и крайнего пессимизма. Данный коэффициент определяется на основе статистических исследований результатов принятия решений или личного опыта принятия решений в схожих ситуациях.

Платежная матрица дополняется столбцом, коэффициенты которого рассчитываются по формуле:

(33)

где

C – коэффициент пессимизма.

Оптимальной по данному критерию считается стратегия, в которой значение W_i максимально:

При С = 1 критерий Гурвица превращается в ММ-критерий. При С = 0 он превращается в критерий «азартного игрока», делающего ставку на то, что выпадет наилучший случай.

Критерий Гурвица применяется в ситуации, когда:

1) информация о состояниях окружающей среды отсутствует или недостоверна;

2) необходимо считаться с появлением каждого состояния окружающей среды;

3) реализуется только малое количество решений;

4) допускается некоторый риск.

Критерий Ходжа–Лемана.

Этот критерий опирается одновременно на ММ-критерий и критерий максимального математического ожидания выигрыша. При определении оптимальной стратегии по этому критерию вводится параметр достоверности информации о распределении вероятностей состояний окружающей среды, значение которого находится в интервале [0, 1]. Если степень достоверности велика, то доминирует критерий максимального математического ожидания выигрыша, в противном случае – ММ-критерий.

Платежная матрица дополняется столбцом, коэффициенты которого определяются по формуле:

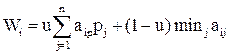. (34)

где

u – параметр достоверности информации о вероятностях состояний окружающей среды.

Оптимальной по данному критерию считается та стратегия, в которой значение W_i максимально:

Данный критерий применим в следующих случаях:

1) если имеется информация о вероятностях состояний окружающей среды, однако эта информация получена на основе относительно небольшого числа наблюдений и может измениться;

2) если принятое решение теоретически допускает бесконечно много реализаций;

3) если при малом числе реализации допускается некоторый риск.

Пример решения статистической игры.

Рассмотрим пример решения статистической игры в экономической задаче.

Сельскохозяйственное предприятие производит капусту. Оно имеет возможность хранить произведенную капусту в течение всего сезона реализации – с осени до начала лета следующего года. Хозяйство может выбрать одну из трех стратегических программ реализации капусты в течение сезона реализации:

A1 – реализовать всю капусту осенью, непосредственно после уборки;

A2 – заложить часть капусты на хранение и реализовать ее в течение осенних и зимних месяцев;

A3 – заложить всю капусту на хранение и реализовать ее в весенние месяцы.

Сумма затрат на производство, хранение и реализацию капусты для хозяйства при выборе им каждой из стратегий составляет соответственно 20, 30 и 40 тыс. денежных единиц.

На региональном рынке капусты может сложиться одна из следующих трех ситуаций:

S1 – поступление капусты на рынок происходит равномерно в течение всего сезона реализации и рынок не испытывает сезонных колебаний цен реализации продукта;

S2 – в осенние месяцы на рынок поступает капусты немного больше, чем зимой и весной. В связи с этим наблюдаются небольшие сезонные колебания цен – в начале зимы цены немного возрастают по сравнению с осенним уровнем и держатся стабильными в течение всех последующих месяцев сезона реализации;

S3 – в осенние месяцы на рынок поступает капусты значительно больше, чем зимой и весной. Объемы капусты, поступающей в течение сезона реализации, постоянно уменьшаются. Поэтому рынок испытывает значительные сезонные колебания цен.

Значения суммы выручки предприятия от реализации капусты при выборе каждой из стратегий реализации и формировании различных ситуаций на рынке представлены в таблице 16.

Таблица 16.

Выручка от реализации капусты, тыс. д.е.

Стратегии хозяйства	Выручка от реализации капусты, тыс. д.е.
	S1	S2	S3
A1	30	25	22
A2	30	40	33
A3	30	40	60

В задаче необходимо:

1. Определить, какая стратегия хозяйства является наиболее выгодной, если известны значения вероятностей состояний рынка капусты региона: 0,3, 0,6 и 0,1 соответственно.

2. Определить, какая стратегия хозяйства является наиболее выгодной, если информация о вероятностях состояний рынка капусты отсутствует и предприятию необходимо:

a) получить минимально гарантированный выигрыш;

b) учесть значения риска от принятия различных решений;

c) определить наиболее выгодную стратегию, если коэффициент пессимизма равен 0,3.

3. Определить наиболее выгодную стратегию, если информация о вероятностях состояний рынка не является вполне достоверной и параметр достоверности информации равен 0,7.

4. Дать экономическую интерпретацию результатов решения задачи.

Решение.

1. Составим платежную матрицу данной игры. Ее коэффициентами будут значения прибыли от производства капусты, получаемые как разница суммы выручки от реализации капусты и затрат на производство, хранение и реализацию капусты (рис. 15).

	S1	S2	S3
A1	10	5	2
A2	0	10	3
A3	-10	0	20

Рис. 15. Платежная матрица задачи определения наиболее выгодной стратегии реализации капусты

2. Определим наиболее выгодную стратегию по критерию максимального математического ожидания выигрыша:

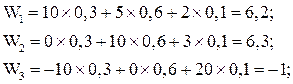
	S1	S2	S3	W_i
P_j	0,3	0,6	0,1
A1	10	5	2	6.2
A2	0	10	3	6.3
A3	-10	0	20	-1

Рис. 16. Определение оптимальной стратегии в статистической игре по критерию максимального математического ожидания

Оптимальной по данному критерию при указанных значениях вероятностей состояния рынка капусты будет стратегия A2 (W = 6,3) (рис. 16).

3. Определим наиболее выгодные стратегии предприятия по ММ-критерию, критерию недостаточного основания Лапласа (НО-критерий) и критерию пессимизма-оптимизма (на рисунке – ПО-критерий, рис. 17).

	S1	S2	S3	W_i (ММ)	W_i (НО)	W_i (ПО)
A1	10	5	2	2	5,67	7,6
A2	0	10	3	0	4,33	7
A3	-10	0	20	-10	3,33	11

Рис. 17. Определение оптимальной стратегии в статистической игре по максиминному критерию, критерию недостаточного основания Лапласа и критерию пессимизма-оптимизма

Значения W_i для ММ-критерия:

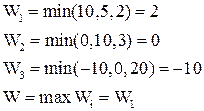
Оптимальной стратегией по максиминному критерию является стратегия A1 (W = 2).

Определим оптимальную стратегию по критерию недостаточного основания Лапласа. По данному критерию оптимальной является стратегия A1 (W = 5,67).

По критерию пессимизма-оптимизма при коэффициенте пессимизма, равном 0,3, оптимальной является стратегия A3 (W = 11).

4. Определим наиболее выгодную стратегию по критерию минимаксного риска. Для этого рассчитаем матрицу рисков (рис. 18).

	S1	S2	S3	R_i
A1	0	5	18	18
A2	10	0	17	17
A3	20	10	20	20

Рис. 18. Определение оптимальной стратегии в статистической игре по критерию минимаксного риска с помощью построения матрицы рисков

Оптимальной стратегией по критерию минимаксного риска является стратегия A2 (W = 17).

5. Определим наиболее выгодную стратегию предприятия по критерию Ходжа–Лемана (рис. 19).

	S1	S2	S3	W_i
P_j	0,3	0,6	0,1
A1	10	5	2	4,94
A2	0	10	3	4,41
A3	-10	0	20	-3,7

Рис. 19. Определение оптимальной стратегии в статистической игре по критерию Ходжа–Лемана

По критерию Ходжа–Лемана оптимальной для хозяйства будет стратегия A1 (W = 4,94).

6. Проведем экономическую интерпретацию результатов решения задачи.

Если предприятие имеет информацию о вероятностях состояния рынка капусты и значения этих вероятностей соответствуют исходным данным задачи, наиболее выгодной стратегией является продажа части капусты в осенние месяцы и хранение оставшейся капусты для реализации в течение зимних месяцев (прибыль составит 6,3 тыс. д.е.). Эта же стратегия является наиболее эффективной, если информация о вероятностях состояний рынка капусты отсутствует и предприятию необходимо минимизировать степень возможного риска потери прибыли в процессе принятия решения (значение возможного риска составит 17 тыс. д.е.).

В случае, когда при отсутствии информации о состоянии рынка наиболее существенным для предприятия является не максимизация прибыли в абсолютном выражении, а получение ее гарантированного объема, хотя бы и минимального, наиболее целесообразным решением является реализация всей капусты в осенние месяцы (прибыль составит 2 тыс. д.е.). Эта же стратегия является наиболее выгодной, если предприятие имеет информацию о вероятностях состояний рынка, соответствующую исходным данным, но эта информация не вполне достоверна (в случае если информация имеет достоверность 0,7, прибыль составит 4,94 тыс. д.е.).

В случае если информация о вероятностях состояний рынка отсутствует и риск значительных потерь не является для предприятия определяющим фактором при принятии решения или если есть основания для оптимистической оценки ситуации на рынке капусты, при котором предприятие имеет возможность получить наибольшую прибыль от производства капусты, ему следует сохранить произведенную продукцию и реализовать ее в весенние месяцы (прибыль составит соответственно 5,7 и 11 тыс. д.е.).

Вопрос 4. Метод экспертных оценок.

Экспертное оценивание – процедура получения оценки проблемы на основе мнения специалистов (экспертов) с целью последующего принятия решения (выбора).

Существует две группы экспертных оценок:

· Индивидуальные оценки основаны на использовании мнения отдельных экспертов, независимых друг от друга.

· Коллективные оценки обобщают субъективные мнения экспертов.

Совместное мнение обладает большей точностью, чем индивидуальное мнение каждого из специалистов. Данный метод применяют также и для получения количественных оценок качественных характеристик и свойств. Например: оценка нескольких технических проектов по степени их соответствия заданному критерию, во время соревнований по фигурному катанию – оценка судьями выступления фигуриста.

Известны следующие методы экспертных оценок:

· Метод ассоциаций. Метод основан на изучении схожего по свойствам объекта с другим объектом.

· Метод парных (бинарных) сравнений. Метод основан на сопоставлении экспертом альтернативных вариантов, из которых надо выбрать наиболее предпочтительные.

· Метод векторов предпочтений. Эксперт анализирует весь набор альтернативных вариантов и выбирает наиболее предпочтительные.

· Метод фокальных объектов. Метод основан на перенесении признаков случайно отобранных аналогов на исследуемый объект.

· Индивидуальный экспертный опрос. Опрос в форме интервью или в виде анализа экспертных оценок. Предполагает беседу заказчика с экспертом, в ходе которой заказчик ставит перед экспертом вопросы, ответы на которые значимы для достижения программных целей. Анализ экспертных оценок предполагает индивидуальное заполнение экспертом разработанного заказчиком формуляра, по результатам которого производится всесторонний анализ проблемной ситуации и выявляются возможные пути ее решения. Свои соображения эксперт выносит в виде отдельного документа.

· Метод средней точки. Формулируются два альтернативных варианта решения, один из которых менее предпочтителен. После этого эксперту необходимо подобрать третий альтернативный вариант, оценка которого расположена между значений первой и второй альтернативы.

Этапы экспертного оценивания:

· Постановка цели исследования.

· Выбор формы исследования, определение бюджета проекта.

· Подготовка информационных материалов, бланков анкет, модератора процедуры.

· Подбор экспертов.

· Проведение экспертизы.

· Статистический анализ результатов.

· Подготовка отчета с результатами экспертного оценивания.

Постановка цели исследования.

Необходимо проверить информацию, проверить точность фактов и достоверность сведений. На странице обсуждения должны быть пояснения.

Экспертное оценивание предполагает использование «коллективного разума», обладающего бóльшими способностями по сравнению с возможностями отдельного человека. Источником возможностей мультиразума является поиск слабых ассоциаций и предположений, основанных на опыте отдельного специалиста. Экспертный подход позволяет решать задачи, не поддающиеся решению обычным аналитическим способом, в том числе такие как:

· выбор лучшего варианта решения среди имеющихся;

· прогнозирование развития процесса;

· поиск возможного решения сложных задач.

Перед началом экспертного исследования необходимо четко определить его цель (проблему) и сформулировать соответствующий вопрос для экспертов. При этом рекомендуется придерживаться следующих правил:

1) Четкое определение условий, времени, внешних и внутренних ограничений проблемы. Возможность ответа на вопрос с доступной человеческому опыту точностью.

2) Вопрос лучше формулировать как качественное утверждение, чем как оценку числа. Для численных оценок не рекомендуется задавать более пяти градаций.

3) Эксперты оценивают возможные варианты, и не следует ожидать от них построения законченного плана действий, развернутого описания возможных решений.

Выбор формы исследования, определение бюджета проекта.

Существующие виды экспертных оценок можно классифицировать по следующим признакам.

· По форме участия экспертов: очное, заочное. Очный метод позволяет сосредоточить внимание экспертов на решаемой проблеме, что повышает качество результата, однако заочный метод может быть дешевле.

· По количеству итераций (повторов процедуры для повышения точности): одношаговые и итерационные.

· По решаемым задачам: генерирующие решения и оценивающие варианты.

· По типу ответа: идейные, ранжирующие, оценивающие объект в относительной или абсолютной (численной) шкале.

· По способу обработки мнений экспертов: непосредственные и аналитические.

· По количеству привлекаемых экспертов: без ограничения, ограниченные. Обычно используется 5–12 человек экспертов.

Наиболее известные методы экспертных оценок: метод Дельфи, мозговой штурм и метод анализа иерархий. Каждому методу соответствуют свои сроки проведения и потребность в экспертах. Метод анализа иерархий был рассмотрен нами выше. Рассмотрим более подробно методологию метода мозгового штурма.

Метод мозгового штурма (мозговой штурм, мозговая атака) – оперативный метод решения проблемы на основе стимулирования творческой активности, при котором участникам обсуждения предлагают высказывать как можно большее количество вариантов решения, в том числе самых фантастичных. Затем из общего числа высказанных идей отбирают наиболее удачные, которые могут быть использованы на практике. Подробнее о методе мозгового штурма было рассказано выше (тема 2, вопрос 3).

После выбора метода экспертного оценивания можно определить затраты на процедуру, которые включают оплату экспертов, аренду помещения, приобретение канцтоваров, оплату специалиста по проведению и анализу результатов экспертизы.

Подготовка информационных материалов.

Эксперты перед вынесением суждения должны разносторонне рассмотреть представленную проблему. Для проведения этой процедуры необходимо подготовить информационные материалы с описанием проблемы, имеющиеся статистические данные, справочные материалы, бланки анкет, инвентарь. Следует избегать следующих ошибок: упоминать разработчиков материалов, выделять тот или иной вариант решения, выражать отношение руководства к ожидаемым результатам. Данные должны быть разносторонними и нейтральными. Заранее необходимо разработать бланки анкет для экспертов. В зависимости от метода они могут быть с открытыми и закрытыми вопросами, ответ может даваться в виде суждении, парного сравнения, ранжированного ряда, в баллах или в виде абсолютной оценки.

Саму процедуру проводит независимый модератор процедуры, который контролирует соблюдение регламента, раздает материалы и анкеты, но сам не высказывает своего мнения.

Подбор экспертов.

Эксперты должны обладать опытом в областях, соответствующих решаемым задачам. При подборе экспертов следует учитывать момент личной заинтересованности, который может стать существенным препятствием для получения объективного суждения. С этой целью, например, применяют метод Шара, когда один эксперт, наиболее уважаемый специалист, рекомендует ряд других и далее по цепочке, пока не будет подобран необходимый коллектив.

Проведение экспертизы.

Проведение процедуры отличается в зависимости от используемого метода. Общие рекомендации:

· Препятствовать давлению авторитетов (эксперт часто боится противоречить мнению большинства или мнению наиболее уважаемого специалиста).

· Установить и соблюдать регламент. Увеличение времени на принятие решения сверх оптимального не повышает точность ответа.

Статистический анализ результатов.

После получения ответов экспертов необходимо провести их оценку. Это позволяет оценить согласованность мнений экспертов. При отсутствии значимой согласованности экспертов необходимо выявить причины несогласованности (наличие групп) и признать отсутствие согласованного мнения (ничтожные результаты).

Оценка ошибки исследования.

Чтобы оценить ошибку исследования, необходимо построить модель свойств объекта на основе ответов экспертов (для аналитической экспертизы). Результаты экспертного оценивания оформляются в виде отчета. В отчете указывается цель исследования, состав экспертов, полученная оценка и статистический анализ результатов.

Вопросы для самопроверки:

1. Дайте определение игры.

2. Дайте определение хода и стратегии.

3. По каким принципам производится классификация игр?

4. Как подразделяются игры по числу игроков?

5. Как подразделяются игры в зависимости от количества стратегий?

6. Как подразделяются игры по характеру взаимодействия между игроками?

7. Как подразделяются игры по виду выигрышей?

8. Как подразделяются игры по виду функции выигрышей?

9. Как записать игру с нулевой суммой в виде платежной матрицы?

10. Что такое нижняя и верхняя цена игры?

11. Что такое оптимальная чистая стратегия? При каких условиях существует оптимальная чистая стратегия?

12. Как уменьшить размерность платежной матрицы?

13. Приведите примеры решения матричных игр в задачах реальной экономики.

14. Существует ли решение матричной игры, нижняя цена которой не равна верхней? Как называется такая игра?

15. Что такое смешанная стратегия игрока?

16. Что такое активная стратегия?

17. Что такое цена матричной игры со смешанным расширением?

18. В каком интервале находится цена матричной игры со смешанным расширением?

19. Каким будет значение выигрыша в матричной игре, если один из игроков придерживается своей оптимальной смешанной стратегии?

20. Что такое решение матричной игры со смешанным расширением?

21. Какими методами решается матричная игра со смешанным расширением?

22. Сформулируйте математическую запись задачи определения оптимальной смешанной стратегии в матричной игре для каждого игрока.

23. Какое преобразование коэффициентов платежной матрицы необходимо произвести перед началом решения матричной игры со смешанным расширением? Каков смысл этого преобразования?

24. Как определить значение цены игры и вероятности выбора стратегий игроков по результатам решения задачи?

25. Приведите примеры решения матричных игр со смешанным расширением в задачах реальной экономики.

26. Что такое статистическая игра? В каких ситуациях возникает необходимость решения статистических игр?

27. Как называется игрок в статистической игре? С чем взаимодействует игрок в статистической игре?

28. Является ли статистическая игра игрой с нулевой суммой?

29. От чего зависит выбор критерия принятия решения в статистической игре?

30. По каким критериям принятия решения определяется наиболее выгодная стратегия ЛПР в ситуации, когда известны вероятности состояний окружающей среды?

31. Какие критерии принятия решения применяются в случае отсутствия информации о вероятностях состояний окружающей среды?

32. Какие критерии принятия решения используются в условиях значительного риска потери выигрыша?

33. Какие критерии принятия решения используются в условиях необходимости получения минимально гарантированного выигрыша?

34. Какие критерии принятия решения используются в условиях недостоверности информации о вероятностях состояний окружающей среды?

35. Что такое критерий азартного игрока? В каких случаях он применяется?

36. Что такое коэффициент пессимизма? Как он определяется?

37. Что такое матрица рисков? Как рассчитываются коэффициенты матрицы рисков?

38. Приведите примеры решения статистических игр в задачах реальной экономики.

39. В каких ситуациях возникает необходимость определения экономического эффекта информации с помощью методов теории игр?

40. Из каких компонентов складывается эффект прогноза для ЛПР?

Литература по теме:

Основная литература:

1. Вентцель Е.С. Исследование операция. – М.: Советское радио, 1972.

2. Воробьев Н.Н. Теория игр для экономистов-кибернетиков. – М.: Наука, 1985.

3. Горелик В.А., Кононенко А.Ф. Теоретико-игровые модели принятия решений в эколого-экономических системах. – М.: Радио и связь, 1982.

4. Давыдов Э.Г. Исследование операций. – М.: Высшая школа, 1990.

Дополнительная литература:

1. Giblons R. Game theory for applied economists. – Princeton University press, Princeton, New Gersey, 1992.

2. Лапшин К.А., Светлов Н.М. Программный комплекс «Линейная оптимизация» – методические указания для студентов экономического факультета. – М.: МСХА, 1994.

3. Лесик А.И., Чистяков Ю.Е. Теоретико-игровые модели взаимодействия экономических субъектов производственной системы. – М.: ВЦ РАН, 1994.

4. Мулен Э. Теория игр с примерами из математической экономики. – М.: Мир, 1985.

5. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр. – М.: Высшая школа, 1998.

6. Платов В.Я. Деловые игры: разработка, организация, проведение. – М.: Профиздат, 1991.

7. Сысоев В.В. Теоретико-игровые модели принятия решений многоцелевого управления в задачах выбора и распределения ресурсов / Воронеж: Воронеж. гос. технол. акад., 2000.