Содержание

 

Аннотация

 

Тема 1. Метод анализа иерархии при согласовании результатов оценки

Вопрос 1. Методология МАИ.

Вопрос 2. Пример применения МАИ при согласовании результатов оценки.

Литература

Основная литература:

Дополнительная литература:

 

Тема 2. Применение MS Excel в целях стоимостной оценки при использовании метода корреляционно-регрессионной зависимости

Вопрос 1. Методология КРА.

Вопрос 2. Расчет рыночной стоимости оцениваемого земельного участка методом математического моделирования.

Литература

Основная литература:

Дополнительная литература:

 

Аннотация

 

Целью изучения дисциплины является формирование у студентов комплексного представления о математических методах в оценке, используемых для согласования результатов оценки стоимости, а также составлению универсальных моделей, позволяющих рассчитать стоимость заданного объекта из обозначенной выборки.

 

Задачи изучения дисциплины:

·     изучение методологии метода анализа иерархии (МАИ);

·     изучение методологии корреляционно-регрессионного анализа (КРА).

 

В результате изучения дисциплины слушатель должен:

 

Знать: методологические принципы, критерии, нормы и правила МАИ и КРА.

 

Уметь использовать полученные знания по математическим методам в оценке в будущей профессиональной деятельности.

 

Иметь представление о возможностях использования рассматриваемых методов в процессе принятия управленческих решений;

 

Тема 1. Метод анализа иерархии при согласовании результатов оценки

 

Цель: изучение методологии метода анализа иерархии при согласовании результатов оценки.

 

Задачи:

·     рассмотреть методологию МАИ;

·     рассмотреть пример применения МАИ при согласовании результатов оценки.

 

 

Вопросы темы:

1.  Методология МАИ.

2.  Пример применения МАИ при согласовании результатов оценки.

 

Вопрос 1. Методология МАИ.

 

Метод Анализа Иерархий (далее - МАИ)  математический инструмент системного подхода к сложным проблемам принятия решений. Основное применение при проведении оценки МАИ находит при осуществлении процедуры согласования полученных результатов по затратному, сравнительному и доходному подходу и расчете итоговой стоимости оцениваемого объекта. Рассмотрим методологию данного математического инструментария более подробно.

МАИ не предписывает лицу, принимающему решение, какого-либо «правильного» решения проблемы, а позволяет ему в интерактивном режиме найти такой альтернативный вариант, который наилучшим образом согласуется с пониманием указанным лицом сути проблемы и требованиями к ее решению. МАИ позволяет понятным и рациональным образом структурировать сложную проблему принятия решений в виде иерархии, а также сравнить и выполнить количественную оценку альтернативных вариантов решения.

Анализ проблемы принятия решений в МАИ начинается с построения иерархической структуры, которая включает цель, критерии, альтернативы и другие рассматриваемые факторы, влияющие на выбор. Эта структура отражает понимание проблемы лицом, принимающим решение. Каждый элемент иерархии может представлять различные аспекты решаемой задачи, причем во внимание могут быть приняты материальные и нематериальные факторы, измеряемые количественные параметры и качественные характеристики, объективные данные и субъективные экспертные оценки. Следующим этапом анализа является определение приоритетов, представляющих относительную важность или предпочтительность элементов построенной иерархической структуры, с помощью процедуры парных сравнений. Безразмерные приоритеты позволяют обоснованно сравнивать разнородные факторы, что является отличительной особенностью МАИ. На заключительном этапе анализа выполняется синтез (линейная свертка) приоритетов на иерархии, в результате которой вычисляются приоритеты альтернативных решений относительно главной цели. Лучшей считается альтернатива с максимальным значением приоритета.

Рассмотрим каждый этап МАИ более подробно.

 

Представление проблемы в виде иерархии.

Вершиной иерархии является главная цель; элементы нижнего уровня представляют множество вариантов достижения цели (альтернатив); элементы промежуточных уровней соответствуют критериям или факторам, которые связывают цель с альтернативами. Существуют специальные термины для описания иерархической структуры МАИ. Каждый уровень иерархии состоит из узлов. Элементы, исходящие из узла, принято называть его «детьми» (дочерними элементами). Элементы, из которых исходит узел, называются родительскими. Группы элементов, имеющие один и тот же родительский элемент, называются группами сравнения. Родительские элементы альтернатив, как правило, исходящие из различных групп сравнения, называются покрывающими критериями. Вид любой иерархии МАИ будет зависеть не только от объективного характера рассматриваемой проблемы, но и от знаний, суждений, системы ценностей, мнений, желаний и т. п. участников процесса. Опубликованные описания применений МАИ часто включают в себя различные схемы и объяснения представленных иерархий. Последовательное выполнение всех шагов МАИ предусматривает возможность изменения структуры иерархии с целью включения в неё вновь появившихся или ранее не считавшихся важными критериев и альтернатив.

Иерархия является полной, если каждый элемент заданного уровня является критерием для всех элементов нижнего уровня (рис. 1).

 

 

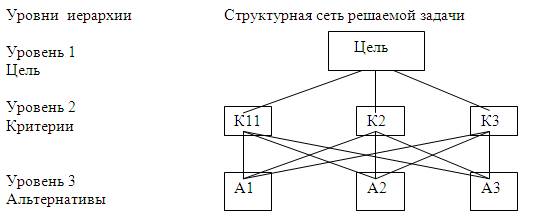
Рис. 1. Полная доминантная иерархия

 

Определение приоритетов критериев.

После иерархического представления задачи необходимо установить приоритеты критериев и оценить каждую из альтернатив по выбранным критериям, определив наиболее важную их них.

Приоритеты  это числа, которые связаны с узлами иерархии. Они представляют собой относительные веса элементов в каждой группе. Подобно вероятностям, приоритеты  безразмерные величины, которые могут принимать значения от нуля до единицы. Чем больше величина приоритета, тем более значимым является соответствующий ему элемент. Сумма приоритетов элементов, подчиненных одному элементу вышестоящего уровня иерархии, равна единице. Приоритет цели по определению равен 1,0.

В МАИ элементы сравниваются попарно по отношению к их влиянию на общую для них характеристику.

Парные сравнения приводят к записи характеристик сравнений в виде квадратной таблицы чисел, т.е. матрицы.

Сравнивая набор критериев друг с другом, получим следующую матрицу:

 

 

 

Эта матрица обратно симметричная, т.е. имеет место свойство:

 

,

 

где индексы i и j - номер строки и номер столбца, на пересечении которых стоит элемент.

При сравнении элемента с самим собой имеем равную значимость, так что на пересечение строки и столбца с одинаковыми номерами заносим единицу. Поэтому главная диагональ будет состоять из единиц.

Таким образом, матрица парных сравнений имеет вид

 

 

 

Когда задача представлена в виде иерархической структуры, матрица составляется для попарного сравнения критериев на втором уровне по отношению к общей цели, расположенной на первом уровне. Такие же матрицы должны быть построены для парных сравнений каждой альтернативы на третьем уровне по отношению к критериям второго уровня и т.д., в зависимости от количества уровней.

Матрица составляется следующим образом.

В левом верхнем углу записывается цель или критерий, по отношению к которым будет проводиться сравнение; в левом столбце и верхней строке необходимо перечислить сравниваемые элементы. Для иерархии, приведенной на рис. 1, потребуется построить четыре матрицы - одну для второго уровня и три для третьего. Эти матрицы представлены в табл. 1 и 2.

 

Таблица 1.

 

Матрица второго уровня

 

 

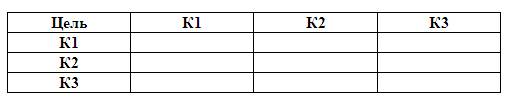
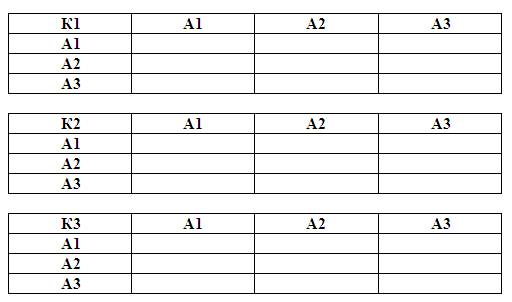
Таблица 2.

 

Матрицы третьего уровня

 

 

Для проведения субъективных парных сравнений в МАИ разработана шкала относительной важности, представленная в табл. 3.

 

Таблица 3.

 

Шкала относительной важности

 

 

При проведении попарных сравнений задаются следующие вопросы:

·          Какая из альтернатив важнее или имеет большее воздействие на цель?

·          Какая из альтернатив более вероятна?

·          Какая из альтернатив предпочтительнее?

·          Какой из критериев более важен?

·          Какая из альтернатив более желательна по отношению к определенному критерию?

·          Какой из сценариев более вероятен?

 

Когда возникают споры, применяют геометрическое среднее разных оценок в качестве общей оценки суждений

 

 

 

Синтез приоритетов.

После построения иерархии и определения величин парных субъективных суждений следует этап, на котором иерархическая декомпозиция и относительные суждения объединяются для получения осмысленного решения многокритериальной задачи принятия решений.

 

Локальные приоритеты.

Из групп парных сравнений формируется набор локальных критериев, которые выражают относительное влияние элементов на элемент, расположенный на уровень выше.

Для определения относительной ценности каждого элемента необходимо найти геометрическое среднее и с этой целью перемножить n элементы каждой строки и из полученного результата извлечь корни n-й степени (1). Полученные числа необходимо нормализовать.

 

     (1)

 

Для нормализации полученных чисел определяем нормирующий множитель r.

 

     (2)

 

И каждое из чисел  делим на .

 

     (3)

 

В результате получаем вектор приоритетов:

 

     (4)

 

где индекс 2 означает, что вектор приоритетов относится ко второму уровню иерархии.

 

Согласованность локальных приоритетов.

Любая матрица суждений в общем случае является не согласованной.

Когда отклонения от согласованности превышают установленные пределы, возникает необходимость определения индекса согласованности и отношения согласованности.

Индекс согласованности (ИС) в каждой матрице и для всей иерархии может быть выражен следующим способом.

Определяется сумма каждого j-го столбца матрицы суждений.

 

     (5)

 

Затем полученный результат умножается на j-ю компоненту нормализованного вектора приоритетов q₂, т.е. сумма суждений первого столбца - на первую компоненту, сумма суждений второго столбца - на вторую и т.д.

 

     (6)

 

Сумма чисел р_j отражает пропорциональность предпочтений, чем ближе эта величина к n (числу объектов и видов действия в матрице парных сравнений), тем более согласованны суждения

 

     (7)

 

Отклонение от согласованности выражается индексом согласованности:

 

     (8)

 

Для определения того, насколько точно ИС отражает согласованность суждений, его необходимо сравнить со случайным индексом согласованности (далее - СИ), который соответствует матрице со случайными суждениями, выбранными из шкалы

 

 

 

при условии равной вероятности выбора любого из приведённых чисел.

В табл. 4 приведены средние значения случайного индекса согласованности (СИ) для случайных матриц суждений разного порядка.

 

Таблица 4.

 

Средние значения СИ для случайных матриц суждений разного порядка

 

 

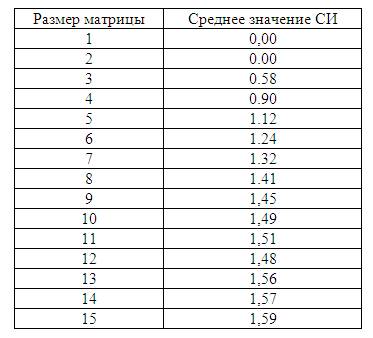
Отношение ИС к среднему значению СИ для матрицы того же порядка называется отношением согласованности (ОС):

 

     (9)

 

Значение ОС меньше или равное 0,10 считается приемлемым.

 

Синтез альтернатив.

Векторы приоритетов и отношения согласованности определяются для всех матриц суждений, начиная со второго уровня вниз.

Для определения приоритетов альтернатив необходимо локальные приоритеты умножить на приоритет соответствующего критерия на вышестоящем уровне и найти суммы по каждому элементу в соответствии с критериями, на которые воздействует этот элемент.

Обозначим через

q_3k - вектор приоритетов k-й матрицы, расположенной на третьем уровне;

q_3ki - i-й элемент вектор приоритетов k-й матрицы суждений, расположенной на третьем уровне;

q_2k- k-й элемент вектор приоритетов  матрицы суждений, расположенной на втором уровне;

q_j - приоритет  j-го элемента третьего уровня.

Тогда приоритет j-го элемента третьего уровня определяется как

 

     (10)

 

Вопрос 2. Пример применения МАИ при согласовании результатов оценки.

 

Данные для расчета возьмем из отчета об оценке, согласно которого, в соответствии с договором  99/06-Ч от 25.05.2006 г., ООО «МАНЭ-МС» произвело оценку специальной стоимости: суммы расходов на возмещение реального ущерба и упущенной выгоды, возникающих вследствие нарушения права по владению имуществом: торговым павильоном ЗАО «МИФ» (табл. 5):

 

Таблица 5.

 

Рыночная стоимость объекта оценки, рассчитанная в рамках различных подходов

 

 

У каждого из подходов есть свои особенности. Например, в большинстве случаев стоимость объекта оценки надежнее всего измеряется суммой получаемых доходов. Однако значительная часть инвесторов, за неимением достоверной аналитической информации, в большей мере ориентируется не на расчётные прогнозные показатели доходного подхода, а на сравнительные рыночные данные.

Стоимости, полученные в рамках разных подходов, могут значительно различаться. В этом случае следует приписать каждому из подходов свой вес, а итоговую величину стоимости определить путем взвешенного усреднения.

В данном примере для определения весов сравнительного и затратного подходов при исчислении итоговой стоимости строений использован МАИ, который является математической процедурой для иерархического представления элементов, определяющих суть любой проблемы.

Расчёт удельных весов каждого подхода с применением МАИ выглядит следующим образом.

1. Выбор критериев:

·     А  возможность отразить действительные намерения инвесторов и продавца;

·     Б  тип, качество, обширность данных, на основе которых проводится анализ;

·     В  способность используемых подходов учитывать конъюнктурные колебания;

·     Г  способность учитывать специфические особенности объекта, влияющие на его стоимость (местонахождение, размер, потенциальная доходность).

2. Построение матрицы сравнения и расчёт приоритетов критериев. Построение матриц парных сравнений в данном пункте и далее проводилось на основе распределения экспертами весов по шкале относительной важности (табл. 6).

 

Таблица 6.

 

Матрица сравнения критериев

 

 

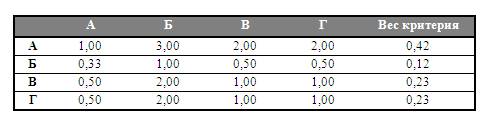
3. Сравнение результатов, полученных затратным (ЗП), сравнительным (СП) и доходным (ДП) подходами по каждому критерию согласования.

3.1. Возможность отразить действительные намерения инвесторов и продавца (критерий А) (табл. 7).

 

Таблица 7.

 

Оценка результатов по критерию А

 

 

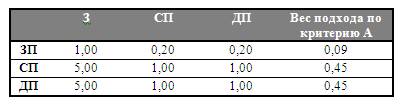
3.2. Тип, качество, обширность данных, на основе которых проводится анализ (критерий Б) (табл. 8).

 

Таблица 8.

 

Оценка результатов по критерию Б

 

 

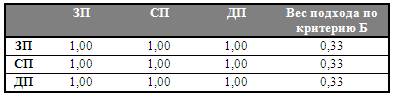
3.3. Способность используемых подходов учитывать конъюнктурные колебания (критерий В) (табл. 9).

 

Таблица 9.

 

Оценка результатов по критерию В

 

 

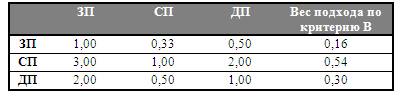
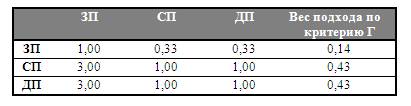
3.4. Способность используемых подходов учитывать специфические особенности объекта, влияющие на его стоимость (критерий Г) (табл. 10).

 

Таблица 10.

 

Оценка результатов по критерию Г

 

 

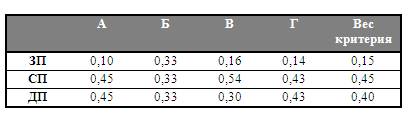
4. Определение итогового значения весов каждого подхода (табл. 11).

 

Таблица 11.

 

Матрица сравнения результатов

 

 

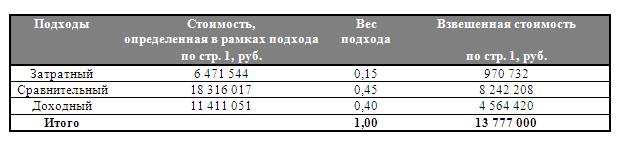
Согласно данным табл. 5 и полученным весам различных подходов, расчет итоговой величины рыночной стоимости объекта оценки будет выглядеть следующим образом (табл. 12).

 

Таблица 12.

 

Расчет итоговой величины рыночной стоимости объектов оценки

 

 

Литература

 

Основная литература:

1.  Кацман В.Е., Косорукова И.В., Родин А.Ю., Харитонов С.В. Основы оценочной деятельности.  М.: МФПУ «Синергия», 2012.  336 с.

 

Дополнительная литература:

1.  Саати Т. Л. Принятие решений при зависимостях и обратных связях: Аналитические сети.  М.: Издательство ЛКИ, 2008.  360 с.

2.  Саати Т. Л. Целочисленные методы оптимизации и связанные с ними экстремальные проблемы.  М.: Мир, 1973.  302 с.

3.  Басакер Р. Г., Саати Т. Л. Конечные графы и сети.  М.: Наука, 1974.  366с.

4.  Саати Т. Л. Принятие решений. Метод анализа иерархий.  М.: Радио и связь, 1989.  316 с.

5.  Саати Т., Кернс К. Аналитическое планирование. Организация систем.  М.: Радио и связь, 1991.  224 с.

 

Тема 2. Применение MS Excel в целях стоимостной оценки при использовании метода корреляционно-регрессионной зависимости

 

Цель: изучение методологии корреляционно-регрессионного анализа применительно к стоимостной оценке.

 

Задачи:

·     рассмотреть методологию КРА;

·     рассмотреть пример применения КРА при проведении стоимостной оценки.

 

Вопросы темы:

1.  Методология КРА.

2.  Пример применения КРА при проведении стоимостной оценки.

 

Вопрос 1. Методология КРА.

 

Согласно ст. 3 Федерального закона от 29.07.1998 г.  135-ФЗ «Об оценочной деятельности в РФ» под оценочной деятельностью понимается профессиональная деятельность субъектов оценочной деятельности (оценщиков  прим. авт.), направленная на установление в отношении объектов оценки рыночной, кадастровой или иной стоимости. Большинство оценок посвящены определению рыночной стоимости  наиболее вероятной цены, по которой объект оценки может быть отчужден на открытом рынке в условиях конкуренции, когда стороны сделки действуют разумно, располагая всей необходимой информацией, а на величине цены сделки не отражаются какие-либо чрезвычайные обстоятельства.

В соответствии с действующим законодательством в области профессиональной оценочной деятельности оценщик при проведении оценки обязан использовать затратный, сравнительный и доходный подходы или обосновать отказ от использования того или иного подхода. Подходом в оценке называют совокупность методов оценки, объединенных общей методологией. Методом оценки является последовательность процедур, позволяющая на основе существенной для данного метода информации определить стоимость объекта оценки в рамках одного из подходов.

Считается, что результат оценки, полученный методами сравнительного подхода, в наибольшей мере отражает величину рыночной стоимости оцениваемого объекта при условии развитого рынка и достаточного объема достоверной и доступной информации о ценах, условиях осуществляемых сделок и характеристик объектов-аналогов. Соответственно, полученное расчетное значение стоимости сравнительным подходом соответствует реальной практике купли-продажи аналогичных объектов оцениваемому объекту.

В каждом направлении оценки принято выделять свои методы оценки в рамках сравнительного подхода. Например, при оценке стоимости бизнеса к методам сравнительного подхода традиционно относят метод рынка капитала, метод сделок, метод отраслевых коэффициентов.

Каждому из методов оценки присущи свои ограничения к применению, преимущества и недостатки. Так как отчет об оценке, подготовленный профессиональным оценщиком, является документом доказательного значения, метод корреляционно-регрессионной зависимости (далее  метод КРЗ), является, пожалуй, одним из наиболее объективных методов сравнительного подхода. Обусловлено это тем, что расчет в рамках данного метода основан на построении корреляционно-регрессионной зависимости между ценами продаж (предложений) объектов-аналогов и каким-либо одним (однофакторная модель) или несколькими (многофакторная модель) параметрами. Тогда, как применяя другие методы сравнительного подхода, оценщику следует вносить либо поправки (корректировки) к ценам объектов-аналогов, которые учитывают имеющиеся у них существенные отличия от объекта оценки (метод сравнения продаж), либо присваивать ранги каждому из критериев сравнения (метод рейтинга-ранжирования). Основным недостатком указанных методов является определенная субъективность производимых расчетов.

Метод КРЗ получил широкое применение при оценке стоимости коммерческой и жилой недвижимости, земельных участков, установок, оборудования и транспортных средств. При этом расчет стоимости данным методом может быть реализован путем построения линейных или нелинейных моделей.

В настоящей статье мы рассмотрим применение метода КРЗ на основе линейной многофакторной модели с использованием средств MS Excel на примере оценки стоимости торговых помещений, расположенных в ЦАО г. Москвы.

Применяя метод КРЗ, оценщику следует выполнить следующую последовательность этапов:

1.  Определить состав ценообразующих факторов.

2.  Подобрать объекты-аналоги.

3.  Выбрать тип регрессионной модели f(х).

4.  Дать оценку параметрам модели.

5.  Построить регрессионную модель.

6.  Проверить адекватность модели.

7.  Рассчитать рыночную стоимость объекта оценки.

 

Этап 1. При проведении анализа рынка торговых помещений г. Москвы, оценщиком было установлено, что основными ценообразующими факторами являются: тип здания, общая площадь помещений, оживленность улицы, линия домов, этаж расположения, наличие отдельного входа и (или) выделенной парковки, состояние помещений.

Поскольку перечисленные факторы являются качественными признаками (кроме общей площади), каждому из них присвоен коэффициент значимости. Если выбранные коэффициенты значимости не обеспечивают значимость уравнения регрессии, то значения коэффициентов подлежат пересмотру. В табл. 13 указаны принятые коэффициенты значимости по ценообразующим факторам.

 

Таблица 13.

 

Коэффициенты значимости ценообразующих факторов объектов-аналогов

 

 

Этап 2. Поиск аналогов осуществляется по предложениям продаж торговых помещений, расположенных в ЦАО г. Москвы в электронных базах данных. Все подобранные объекты-аналоги расположены в жилых домах на первой линии и не имеют выделенной парковки. Поскольку перечисленные ценообразующие факторы по всем объектам-аналогам и объекту оценки идентичны, они исключены из модели.

 

Характеристики объектов-аналогов и объекта оценки приведены на рис. 2.

 

 

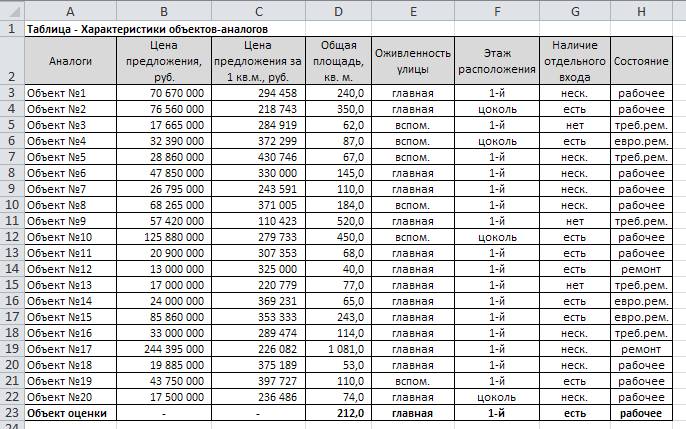
Рис. 2. Характеристики объекта оценки и объектов-аналогов

 

Этап 3. Неизвестную функцию f(х) в окрестностях точки, соответствующей средним уровням каждого фактора, можно представить отрезком степенного ряда. Так как интервалы варьирования факторов невелики, то можно ограничиться линейным приближением в виде полиномиальной модели. Уравнение множественной линейной регрессии описывается формулой:

 

,     (11), где

 

y  значение результирующего признака, полученное в результате подстановки соответствующих значений факторных признаков в уравнение регрессии;

x₁, x₂, …, x_n  факторные признаки;

a₁, a₂, …, a_n  параметры модели (коэффициенты модели).

 

Этап 4. В табл. 13 указан состав основных ценообразующих факторов, и определены величины коэффициентов значимости, оценивающих качественные признаки объектов-аналогов. Если объект-аналог превосходит объект оценки по какому-либо параметру, то ему присваивается больший коэффициент значимости и наоборот. На основании качественных характеристик объекта оценки и объектов-аналогов, составлена таблица, в которой показаны сводные данные о характеристиках объектов-аналогов, выраженные количественными значениями коэффициентов значимости (рис. 3).

 

 

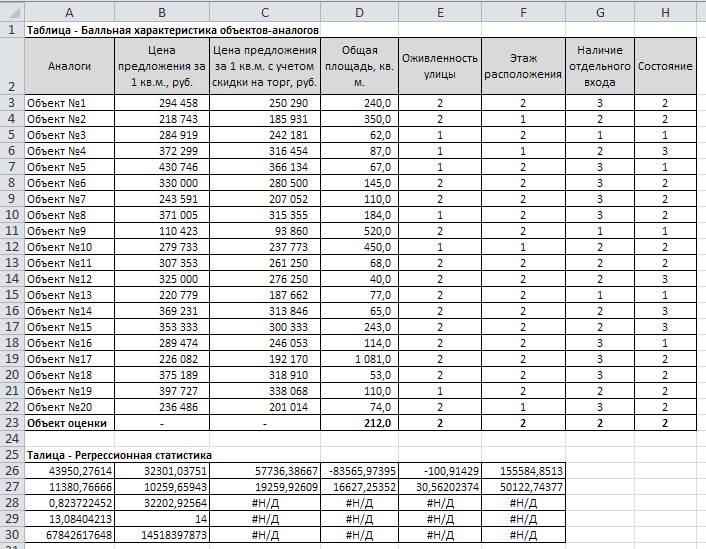
Рис. 3. Балльная характеристика объектов-аналогов и регрессионная статистика

 

Поскольку анализировались цены предложения, а не продажи, т.е., для проведения расчетов собрана информация о еще не состоявшихся сделках, то к ценам предложения применялась скидка на торг в размере 15%.

Зависимой переменной в данном случае является величина рыночной стоимости 1 кв.м. площади объектов-аналогов. Независимые данные являются качественными характеристиками.

Этап 5. Для построения множественной линейной регрессии следует воспользоваться встроенной функцией ЛИНЕЙН. В качестве результата данная функция заполняет блок ячеек А26:F30 (рис. 3). В справке к рассматриваемой функции смысл ее применения и интерпретация полученных результатов объясняется достаточно хорошо. Тем не менее, мы решили в табл. 14 привести в каком порядке возвращается дополнительная регрессионная статистика.

 

Таблица 14.

 

Порядок возращения дополнительной регрессионной статистики

 

 

a₀, a₁, …,a₅  коэффициенты, соответствующие каждой независимой переменной;

se₀, se₁, …,se₅  стандартные значения ошибок, для коэффициентов a₀, a₁, …, a₅;

R²  коэффициент детерминации;

F  наблюдаемое значение коэффициента Фишера;

d_f  степени свободы;

ss_рег  регрессионная сумма квадратов;

ss_ост.  остаточная сумма квадратов.

 

Синтаксис функции: ЛИНЕЙН (известные_значения_y., [известные_значения_x.], [конст], [статистика]). Параметр «известные_значения_y»  обязательный аргумент, который представляет диапазон ячеек со значениями зависимой переменной. Параметр «известные_значения_x»  необязательный аргумент, отражающий значения независимой переменной. Параметры «конст» и «статистика» также являются необязательными. Если параметр «конст» опущен или для него установлено значение ИСТИНА (как в приведенном примере), то регрессия вычисляется обычным образом. Если данный параметр установлен равным нулю, тогда отрезок регрессии принудительно устанавливается равным нулю. Если для параметра «статистика» задано значение ИСТИА (как в приведенном примере), то вычисляется дополнительная регрессионная статистика. В противном случае  только отсекаемый отрезок и угловой коэффициент (наклон).

Формула функции ЛИНЕЙН вводится как формула массива, поэтому для ее применения следует выделить область ячеек. В нашем случае это А26:F30(рис. 2). При выборе размера области ячеек следует руководствоваться тем, что количество строк по данной функции всегда составляет 5, а количество столбцов равно x_n+ 1. Затем необходимо вписать саму формулу функции =ЛИНЕЙН(C3:C22;D3:H22;;ИСТИНА)) и нажать комбинацию клавиш <Ctrl+Shift+Enter>.

Этап 6. Основным критерием, характеризующим адекватность регрессионной модели, является коэффициент детерминации  R². Значения данного показателя позволяют судить о том, какой процент дисперсии известных рыночных данных объясняется с помощью регрессионной зависимости. Значение коэффициента детерминации, близкое к 1,0, показывает, что модель объясняет почти всю изменчивость соответствующих переменных.

В практических задачах оценка качества модели по показателю R²считается очень высокой, если его значения достигают значений 0,9 и выше, и достаточной при значениях, соответствующих 0,7 и выше.

В соответствии с приведенными расчетами на рис. 2, найденная связь между ценами предложений объектов-аналогов и основными ценообразующими факторами удовлетворяет критерию достаточности. Согласно шкале Чеддока полученное значение коэффициента детерминации в 0,82 (ячейка А28, рис. 3) свидетельствует о сильной прямой зависимости.

Чтобы определить, является ли результат R² случайным, следует проанализировать F-статистику (коэффициент Фишера). Предположим, что на самом деле нет взаимосвязи между переменными, а просто были выбраны редкие аналоги, для которых статистический анализ вывел сильную взаимозависимость. Коэффициент Фишера используется для обозначения вероятности ошибочного вывода о том, что имеется сильная взаимозависимость. Если F-наблюдаемое больше, чем F-критическое, то взаимосвязь между переменными имеется. F-критическое можно получить из таблицы F-критических значений в любом справочнике по математической статистике.

Наблюдаемое значение коэффициента Фишера, равное 13,08 (ячейка А29, рис. 3) больше, чем критическое, которое составляет при уровне значимости 0,95 значение в 4,46. Следовательно, полученное регрессионное уравнение полезно для расчета стоимости оцениваемых торговых помещений.

Этап 7. Получив коэффициенты регрессионной зависимости, можно вычислить значение стоимости 1 кв.м площади Y для объекта оценки (ячейка B3) путем подстановки в формулу множественной линейной регрессии (11) значения x₁, x₂,…, x_n,соответствующих характеристикам оцениваемого помещения, указанных в таблице на рис. 2.

Расчет рыночной стоимости объекта оценки приведен на рис. 4.

 

 

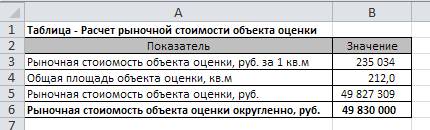
Рис. 4. Расчет рыночной стоимости объекта оценки

 

Рыночная стоимость объекта оценки (ячейка B5) определена как произведение полученного значения рыночной стоимости за 1 кв.м и общей площади объекта оценки: B5=B3*B2. В ячейке B6 приведено округленное значение рыночной стоимости оцениваемого торгового помещения: B6=ОКРУГЛ(B5;-4).

 

Вопрос 2. Расчет рыночной стоимости оцениваемого земельного участка методом математического моделирования.

 

Для определения рыночной стоимости оцениваемого земельного участка была построена регрессионная модель, описывающая взаимодействие основных ценообразующих факторов. Для этого, оценщиком была собрана информация о цене предложений земельных участков, расположенных в центральной части г. Кисловодска, аналоги, составившие первоначальную выборку, представлены в таблице ниже:

 

Таблица 15.

 

Выборка предложений продажи земельных участков в центральной части г. Кисловодска

 

 

Для построения регрессионной модели необходима оцифровка имеющейся информации по основным ценообразующим факторам. По мнению оценщика, таковыми являются: местоположение участка, его размер, передаваемые в ходе сделки права (право собственности или аренды) и назначение участка. Доступные коммуникации не были выделены в качестве ценообразующего фактора, поскольку все аналоги в выборке имеют доступ ко всем необходимым коммунальным услугам.

Фактор «местоположение» описывался исходя из удаленности земельного участка от центра города, в качестве отправной точки была выбрана Колоннада  центральный вход в Кисловодский курортный лечебный парк, как место, наиболее привлекательное в г.Кисловодске с точки зрения цен на земельные участки. Таким образом, фактор является количественным и представляет собой удаленность в метрах аналога от Колоннады.

Размер участка  количественный фактор, представляет собой площадь земельного участка в квадратных метрах.

Передаваемые права  данный фактор носит качественный характер и для его описания применено ранжирование  аналогам, подразумевающим передачу права собственности на участок, присвоено значение 1, права аренды  0.

Назначение участка  в представленной выборке все участки разделены на две группы  предназначенные для индивидуального жилищного строительства и для коммерческого строительства. Всем аналогам из первой группы присвоено значение 0, из второй  1.

Оцифрованная информация по выборке представлена в таблице ниже, объекты отранжированы по степени возрастания цены предложения за 1 кв.м.

 

Таблица 16.

 

Исходная информация по аналогам и объекту оценки

 

 

Следующим шагом является проверка наличия зависимости между каждой факторной переменной и результирующим показателем (цена предложения). Для оценки степени зависимости количественных переменных рассчитывался коэффициент корреляции. Расчет производился в среде MS Excel:

 

Таблица 17.

 

Корреляция количественных факторов с результирующим показателем

 

 

Полученные значения корреляции свидетельствуют о существовании ярко выраженной очень тесной связи между расположением участка и ценой предложения, корреляция между размерами участка и ценой предложения за 1 кв.м участка практически отсутствует.

Для ранговых факторов проверка значимости влияния производилась с помощью однофакторного дисперсионного анализа. при расчете использовались встроенные возможности MS Excel («Сервис» → «Анализ данных» → «Однофакторный дисперсионный анализ»).

 

Таблица 18.

 

Проверка значимости влияния качественных факторов

 

 

По итогам проверки можно сделать вывод о предполагаемой значимости влияния назначения участка на его удельную стоимость. Однако, стоит отметить, что в выборке аналогов преобладают участки предназначенные для индивидуального жилищного строительства (10 из 15), подобный дисбаланс может повлиять на адекватность расчетов значимости данного фактора.

В результате проверки тесноты связи между результирующим показателем и всеми отобранными ценообразующими факторами, мы пришли к выводу, что на значение стоимости оказывают влияние только местоположение участка и его назначение. В качестве функциональной зависимости для регрессионной модели выбрана линейная зависимость вида:

 

,

 

где:

y  результирующая переменная (цена предложения з/у, руб./кв.м);

x₁  расстояние до кисловодской Колоннады, м;

x₂  назначение земельного участка.

Исходные данные для построения многофакторной модели будут иметь вид:

 

Таблица 19.

 

Выборка для построения многофакторной регрессионной модели

 

 

Определение параметров модели осуществлялось методом наименьших квадратов с помощью MS Excel («Сервис» → «Анализ данных» → «Регрессия»). Все параметры и показатели качества полученной модели представлены ниже.

 

Таблица 20.

 

Регрессионная статистика

 

 

Таблица 21.

 

Дисперсионный анализ

 

 

Таблица 22.

 

Описание полученной двухфакторной регрессионной модели

 

 

Таким образом, искомая двухфакторная регрессионная модель имеет вид:

 

 

 

Анализ показателей качества полученной модели

 

1) Коэффициент детерминации R²=0,875, следовательно, полученная модель на 87,5% объясняет изменение стоимости под влиянием включенных в модель факторных переменных. Это высокое значение для данного показателя. Коэффициент детерминации всегда лежит в интервале от 0 до 1. Чем ближе значение коэффициента детерминации к единице, тем лучше модель описывает исходный ряд данных.

2) Скорректированный коэффициент детерминации R²_cкор=0,855, за счет поправки величина коэффициента детерминации существенно не уменьшилась, что подтверждает сделанный ранее вывод о хорошем качестве модели.

3) F-критерий. С помощью F-критерия проводится проверка значимости уравнения регрессии в целом. Эта процедура сводится к проверке статистической значимости коэффициента детерминации R², то есть проверяется нулевая гипотеза R²=0. Эта гипотеза равносильна гипотезе  =  = … =  = 0, F-критерий используется как «пароль»: если коэффициент R² значим, следовательно, связь между y и факторными переменными действительно существует и можно приступать к ее объяснению. Если же коэффициент R² незначим, то данные представляют собой набор не связанных между собой случайных чисел. Однако это еще не значит, что зависимости нет, возможно, просто исходных данных не достаточно для того, чтобы она проявилась. Если показатель значимости F меньше 0,05, то полученный результат является значимым. Если значимость F меньше 0,01, тогда полученный результат является высоко значимым. Если же значимость F больше 0,05, то модель является статистически незначимой. В нашем случае уровень значимости F-критерия составляет 3,75123Е-06 = 3,751×10^-6, так как данное значение существенно меньше 0,01, то полученная модель является высоко значимой.

4) Проверка статистической значимости параметров уравнения регрессии проводится с помощью t-критерия (критерия Стьюдента). Оценить статистическую значимость коэффициента регрессии  означает определиться, существенно ли влияет факторная переменная x_j в генеральной совокупности на результирующую переменную y, то есть, отличается ли истинное (но неизвестное) значение коэффициента  от нуля. Для статистической проверки этой гипотезы применяется t-критерий. Если построение регрессионной модели проводится с помощью MS Excel, то проверить t-критерий проще всего, отыскав в результатах расчета значения значимости t для каждого коэффициента . Если это значение меньше 0,05, то соответствующий коэффициент  является значимым. Если p-значение меньше 0,01, тогда соответствующий коэффициент является высоко значимым. Если же p-значение для какого-либо коэффициента  больше 0,05, то он является статистически незначимым. Незначимость коэффициента  означает, что факторная переменная x_j существенно не влияет на результирующую переменную y. В нашем случае уровни значимости t-критерия (p-значения) для коэффициентов  и  существенно меньше 0,01, что свидетельствует об их высокой значимости. Исключение составляет переменная x₂ (передаваемые права), так как p-значения для коэффициента при данной переменной больше 0,05.

5) Кроме проверки статистической значимости параметров уравнения регрессии можно также проанализировать их доверительные интервалы. Доверительный интервал  это числовой промежуток, в который с вероятностью  попадает истинное значение коэффициента регрессии. Доверительный интервал является интервальной оценкой. Интервальная оценка в отличие от точечной оценки дает ценную информацию о надежности полученных результатов, поэтому в целях повышения достоверности и обоснованности, приводимых в отчетах выводов и умозаключений, процедуры построения доверительных интервалов для всех оцениваемых параметров должны осуществляться всегда. В таблице, формируемой MS Excel при выполнении функции «Регрессия» уже приведены левые и правые границы доверительных интервалов при  для всех коэффициентов уравнения регрессии. Границы доверительного интервала коэффициентов регрессии не должны содержать противоречивых результатов, т.е. левая и правая границы должны быть одновременно либо отрицательными, либо положительными числами. Удобно пользоваться следующим правилом: если доверительный интервал включает нулевое значение, то принимается гипотеза о статистической незначимости соответствующего показателя. В нашем случае, доверительный интервал для коэффициента  имеет вид: . Ноль принадлежит данному промежутку, следовательно, коэффициент  статистически незначим.

Таким образом, полученная модель имеет очень хорошие показатели качества. Однако данный вариант нельзя считать окончательным, так как есть проблема статистической незначимости коэффициента  при переменной x₂. Этот факт свидетельствует, что в данном случае при неизменных значениях остальных факторных переменных (в данном случае  местоположения), отсутствуют доказательства сколько-нибудь значимого влияния на стоимость 1 кв.м. земельного участка, его назначения.

В итоге, после комплексного рассмотрения влияния на цену предложения 1 кв.м. земельного участка в центральной части г. Кисловодска, 4-х ценообразующих факторов, можно сделать вывод, что основной факторной переменной является расположение земельного участка, в нашем случае, описываемое как расстояние до кисловодской Колоннады. Таким образом, модель сведена до однофакторной регрессии, в качестве факторной переменной  расстояние до Колоннады в метрах, зависимая переменная  цена предложения за 1 кв.м. земельного участка, руб. По имеющейся выборке был построен точечный график и описывающие зависимость функции средствами MS Excel.

 

 

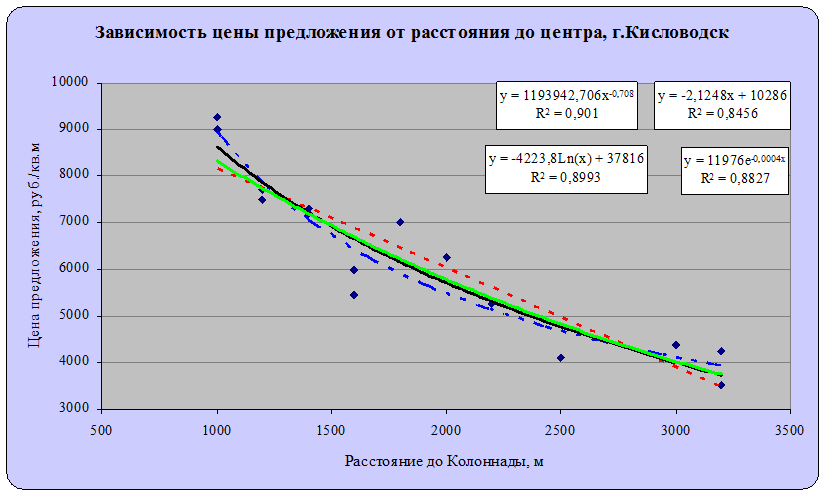
Рис. 5. Зависимость цены предложения за 1 кв.м земельного участка от его расположения

 

Как видно из представленного графика наибольшим коэффициентом детерминации обладает степенная зависимость (R²=0,901). Поэтому в качестве регрессионной модели была выбрана однофакторная степенная зависимость вида:

 

 

 

Коэффициент детерминации равен 0,901, что свидетельствует о высокой статистической значимости построенной регрессионной модели.

 

Литература

 

Основная литература:

1.  Кацман В.Е., Косорукова И.В., Родин А.Ю., Харитонов С.В. Основы оценочной деятельности.  М.: МФПУ «Синергия», 2012.  336 с.

 

Дополнительная литература:

1.  Саати Т. Л. Принятие решений при зависимостях и обратных связях: Аналитические сети.  М.: Издательство ЛКИ, 2008.  360 с.

2.  Саати Т. Л. Целочисленные методы оптимизации и связанные с ними экстремальные проблемы.  М.: Мир, 1973.  302 с.

3.  Басакер Р. Г., Саати Т. Л. Конечные графы и сети.  М.: Наука, 1974.  366с.

4.  Саати Т. Л. Принятие решений. Метод анализа иерархий.  М.: Радио и связь, 1989.  316 с.

5.  Саати Т., Кернс К. Аналитическое планирование. Организация систем.  М.: Радио и связь, 1991.  224 с.