ТЕМА 7. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

7.1. Линейные электрические цепи постоянного тока

Изучив вопросы по теме 7.1., вы будете

Знать:

· отличия между идеальным и реальным источником напряжения (тока);

· взаимосвязь между ЭДС, напряжением, потребляемым током, внутренним сопротивлением источника и сопротивлением нагрузки;

· способы эквивалентных преобразований электрических цепей.

Уметь:

· рассчитывать напряжение на зажимах источника ЭДС и ток, создаваемый источником тока во внешней цепи;

· определять сопротивление цепи, составленной из включенных последовательно и параллельно потребителей энергии;

· преобразовывать схему включения потребителей энергии звездой в эквивалентную схему включения треугольником и наоборот;

· рассчитывать токи и падения напряжения на участках цепей.

Акцентировать внимание на следующих понятиях:

· электрическая цепь;

· источник и потребитель энергии;

· электродвижущая сила;

· идеальный источник напряжения (тока);

· реальный источник напряжения (тока);

· внутреннее сопротивление источника;

· внутренняя проводимость источника;

· активный (пассивный) двухполюсник;

· последовательное соединение потребителей энергии;

· параллельное соединение потребителей энергии;

· соединение потребителей энергии звездой;

· соединение потребителей энергии треугольником.

7.1.1. Источники и потребители электрической энергии постоянного тока

Электрическая цепь представляет собой совокупность электротехнических устройств, создающих путь для электрического тока, электромагнитные процессы в которых описываются уравнениями с учетом понятий об электродвижущей силе, электрическом токе и электрическом напряжении.

Основными элементами электрической цепи (рис. 7.1) являются источники и потребители электрической энергии. В качестве источников электрической энергии постоянного тока широко распространены генераторы постоянного тока и гальванические элементы. Источники электрической энергии характеризуются ЭДС Е, которую они развивают, и внутренним сопротивлением R₀.

Потребителями электрической энергии являются резисторы, электрические двигатели, электролизные ванны, электрические лампы и т. д. В них электрическая энергия преобразуется в механическую, тепловую, световую и др. В электрической цепи за положительное направление ЭДС Е принимается направление, совпадающее с силой, действующей на положительный заряд, т. е. от «-» источника к «+» источника питания. За положительное направление напряжения U принято направление, совпадающее с направлением действия электрического поля, т. е. от «+» к «-» источника. За положительное направление тока I принято направление, совпадающее с перемещением положительных зарядов, т. е. от «+» к «-» источника.

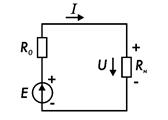
Рис. 7.1.

В электрической цепи электродвижущая сила ЭДС источника может иметь одинаковое и противоположное направление с током. В первом случае источник ЭДС работает в режиме генератора, т. е. является источником электрической энергии. При этом ЭДС Е оказывается большей напряжения на его зажимах (Е > U). При направлении ЭДС Е в цепи противоположном току источник становится потребителем электрической энергии, т. е. он работает в режиме потребителя и при этом ЭДС Е оказывается меньше напряжения U на зажимах источника (Е < U) на величину внутреннего падения напряжения R₀I. При расчетах электрических цепей реальные источники электрической энергии заменяются схемами замещения.

В теории цепей для представления источников электрической энергии используют две модели: идеальные источники напряжения и идеальные источники тока. С их помощью посредством схем замещения описывают реальные источники электрической энергии.

7.1.2. Идеальные источники напряжения (источники ЭДС)

Идеальный источник напряжения (синонимы - источник ЭДС, генератор ЭДС) представляет собой активный двухполюсник, вырабатывающий напряжение, которое не зависит от тока, протекающего через этот двухполюсник. ЭДС - аббревиатура термина электродвижущая сила. В теории цепей рассматривают источники постоянной ЭДС и источники переменной ЭДС, изменяющейся во времени по определенному закону. Источник ЭДС и его вольтамперная характеристика (ВАХ) показаны на рис. 7.2, а, б. На электрических схемах цепей с гальваническими элементами (батарейками, аккумуляторами) обычно используют особые обозначения для источников постоянной ЭДС (рис. 7.2, в). Если знаки «плюс» и «минус» около полюсов такого элемента не расставлены, следует считать, что электрод, обозначенный длинной полосой, имеет более высокий («плюсовой») потенциал.

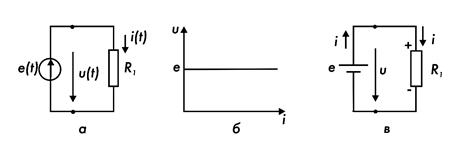
Рис. 7.2. Идеальный источник ЭДС и его ВАХ

Напряжение между полюсами идеального источника напряжения появляется вследствие действия сторонней силы, которая переносит заряды внутри источника. Причем положительные заряды движутся от полюса с меньшим потенциалом к полюсу с большим потенциалом - от «минуса» к «плюсу». Отрицательные заряды движутся в обратном направлении. В условном обозначении источника ЭДС присутствует стрелка. Она играет роль опорного (условного положительного) направления для источника ЭДС. Условились считать, что электродвижущая сила направлена туда, куда движутся внутри источника положительные заряды, - от «минуса» к «плюсу». Во внешней цепи ток положительных зарядов направлен от вывода «плюс» источника ЭДС к выводу «минус». Перемещение единичного положительного заряда по цепи между этими полюсами сопровождается выполнением работы, численно равной напряжению, которое отсчитывается от «плюса» к «минусу». Такую же работу совершает внутри источника электродвижущая сила. Если направления отсчета напряжения и ЭДС выбраны так, как показано на рис. 7.2, а (стрелки направлены противоположно), то:

u(t) = e(t).

Если стрелки для ЭДС и напряжения на источнике направлены в одну сторону, следует пользоваться равенством:

u(t) = -e(t).

При любом выборе опорных направлений ЭДС и напряжения расчет мгновенной мощности показывает, что для источника ЭДС она отрицательна (энергия отдается), а для подключенной к нему внешней цепи (например, для сопротивления R₁ на рис. 7.2, а) - положительна.

Недопустимо рассматривать случай «закорачивания» источника ЭДС, поскольку такая ситуация противоречит положениям теории цепей: с одной стороны, между точками подключения идеально проводящего провода напряжение должно быть нулевым, а с другой стороны, поскольку эти точки являются полюсами источника ЭДС, оно обязано равняться значению ЭДС.

7.1.3. Реальные источники напряжения

Напряжение на выводах реального источника электрической энергии уменьшается с увеличением тока. Вольтамперная характеристика такого источника (рис. 7.3, а) идет с наклоном. Данное обстоятельство можно учесть, включив последовательно с источником ЭДС сопротивление R₀ (рис. 7.3, б). Его называют внутренним сопротивлением источника (генератора). При таком представлении напряжение на полюсах реального источника напряжения равно:

u = e – iR_0.

Оно, как видно, зависит от протекающего через источник тока - при постоянном сопротивлении R₀ напряжение и линейно падает с ростом тока (предположение о неизменности R₀, хотя и весьма условно, однако может быть принято для многих реальных источников.) Стоит отметить, что такой источник напряжения будет отдавать во внешнюю цепь мощность конечного значения при любой нагрузке, то есть при любом значении сопротивления R₁. Его даже можно замкнуть накоротко.

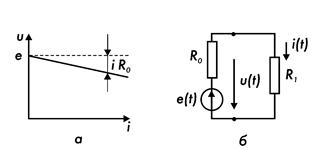
Рис. 7.3. Реальный источник ЭДС и его ВАХ

Чтобы активные двухполюсники играли в устройствах роль источников ЭДС, их вольтамперные характеристики должны спадать слабо. То есть падение напряжения на внутреннем сопротивлении источника (iR₀) для любых протекающих в цепи токов должно быть существенно меньше его ЭДС. Это достигается при малости сопротивления R₀ по сравнению с теми сопротивлениями, которые подключаются к полюсам источника.

7.1.4. Идеальный и реальный источники тока

Идеальный источник, или генератор, тока — активный двухполюсник, ток через который не зависит от напряжения на его зажимах. Обозначение источника тока на схеме с подключенной к нему нагрузкой (сопротивлением), а также вольтамперная характеристика для него представлены на рис. 7.4. Несложно показать, что мгновенная мощность, отдаваемая источником тока во внешнюю цепь, будет отрицательной - свойство, присущее активному элементу.

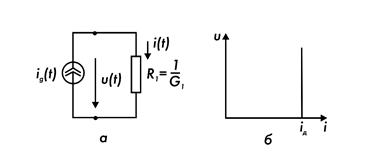
Рис. 7.4. Идеальный источник тока и его ВАХ

Положение о неизменности тока идеального источника при изменении напряжения на его полюсах справедливо, естественно, и для нулевого напряжения и. Это случается при нулевом сопротивлении нагрузки или бесконечной проводимости, то есть когда реализован режим короткого замыкания. (Сокращенное обозначение для режима короткого замыкания – к.з.) Размыкание источника тока недопустимо, поскольку противоречит положениям теории цепей. Действительно, ток источника обязан течь по ветви, но ветвь разорвана. Отметим, что данный запрет аналогичен недопустимости короткого замыкания выводов источника ЭДС.

Ток, вырабатываемый реальным источником электрической энергии, уменьшается с ростом напряжения (рис. 7.5). Данное обстоятельство можно учесть, подключив параллельно идеальному источнику тока i_g проводимость G_g, которую называют внутренней проводимостью источника тока. Получаем представление источника электрической энергии в виде реального источника тока. Уравнение ВАХ реального источника тока имеет вид:

i = i_g - uG_g

Напряжение на полюсах такого источника и мощность, отдаваемая во внешнюю цепь, всегда конечны. Для реального источника тока допустим режим холостого хода (сокращенно - хх), поскольку ток генератора при этом режиме замыкается через внутреннюю проводимость.

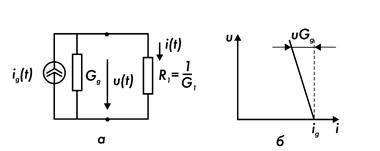
Рис. 7.5. Реальный источник тока и его ВАХ

7.1.5. Эквивалентность различных представлений источника электрической энергии

На основании вышеизложенного можно сделать заключение о допустимости представления реального источника электрической энергии двояким образом - последовательной цепью, содержащей источник ЭДС, или параллельной цепью, содержащей генератор тока. В случае постоянных токов для схемы, изображенной на рис. 7.5, справедливо:

u = ig/G_g – i/G_g.

Для схемы, изображенной на рис. 7.3, имеем: и = e – iR₀. При выполнении условий G_g = 1/R₀ и i_g = e/R₀ одну схему можно заменить другой. При этом ток на полюсах схемы реального источника и напряжение между его полюсами не изменятся. Следовательно, обе схемы замещения для источника энергии можно считать эквивалентными по отношению к внешней цепи (эквивалентность понимается именно в этом смысле.)

Поскольку для реального источника энергии допустимы режимы холостого хода и короткого замыкания (по крайней мере мысленно), можно по вычислениям напряжения холостого хода u_хх на выводах источника и тока короткого замыкания i_кз в проводе, закорачивающем выводы источника, найти значения элементов, входящих в обе схемы замещения реального источника энергии. А именно:

e = u_хх, i_g = i_кз, R₀ = u_хх/i_кз, G_g = 1/R₀.

В случае переменных токов также можно представлять источники электрической энергии эквивалентными схемами, содержащими идеальный источник напряжения или идеальный источник тока.

Вариантностью схемного отображения удобно пользоваться при расчетах, выбирая для источника энергии наиболее подходящее для конкретного случая представление. Например, если сопротивление R₀ реального источника мало по сравнению с другими сопротивлениями схемы, целесообразно представлять источник энергии источником напряжения. Если проводимость G_g реального источника мала по сравнению с другими проводимостями схемы, целесообразно представлять источник энергии источником тока.

Соединив последовательно источник напряжения, близкий по свойствам источнику ЭДС, и резистор, имеющий большое сопротивление, можно составить активный двухполюсник, похожий на идеальный источник тока. Действительно, чтобы реальный источник тока приближенно походил на идеальный, его внутренняя проводимость должна быть много меньше проводимости внешней цепи. То есть для схемы, изображенной на рис. 7.5, должно выполняться соотношение G_g« G₁. Это получится, если последовательно с источником ЭДС (рис. 7.3) включить сопротивление R₀ настолько большое, чтобы выполнялось условие R₀ >> R₁. Тогда ток в цепи практически не будет зависеть от значения сопротивления нагрузки:

i = e/(R₀ + R₁) ≈ e/R₀,

что характерно для идеального источника тока.

Для участка цепи, не содержащего источник энергии (например, для схемы рис. 7.6), связь между током и напряжением U₁₂определяется законом Ома для участка цепи:

где j₁ и j₂ — потенциалы точек 1 и 2 цепи (j₁ > j₂); U₁₂ = j₁ - j₂ - напряжение (разность потенциалов) между точками 1 и 2 цепи; ∑R - арифметическая сумма сопротивлений на участке цепи; R₁ и R₂ — сопротивления участков цепи.

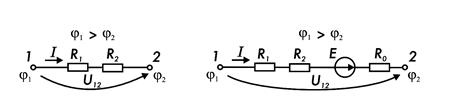
Рис. 7.6 Рис. 7.7.

Для участка цепи, содержащей источник энергии (рис. 7.7), закон Ома записывают в виде выражения

где Е - ЭДС источника энергии;

∑R = R₁ + R₂ - арифметическая сумма сопротивлений R₁и R₂ участков цепи;

R₀ - внутреннее сопротивление источника энергии.

Взаимосвязь между всеми видами мощностей в электрической цепи (баланс мощностей) определяется из уравнения:

∑P₁= ∑P₂ + ∑P_n,

где ∑P₁- алгебраическая сумма мощностей источников энергии (∑P₁ = ∑EI);

∑P₂- алгебраическая сумма мощностей потребителей электроэнергии;

∑P_n- суммарная мощность, обусловленная потерями в сопротивлениях источника (∑P_n= ∑I ²R₀).

Резисторы, а также сопротивления других электротехнических устройств являются потребителями электрической энергии. Баланс мощностей определяется законом сохранения энергии, при этом в любой замкнутой электрической цепи алгебраическая сумма мощностей источников энергии равна алгебраической сумме мощностей, расходуемых потребителями электрической энергии.

Коэффициент полезного действия установки определяется отношением

h = Р₂/Р₁.

Пример.

Определить напряжение U на зажимах аккумулятора с ЭДС Е = 2 В и внутренним сопротивлением R₀ = 0,01 Ом, мощность, отдаваемую нагрузочному резистору при разрядке, и мощность, потребляемую им при зарядке при токе I = 10 А.

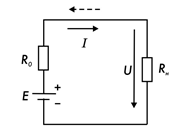
Рис. 7.8.

Решение. Схема электрической цепи с аккумулятором при разрядке приведена на рис. 7.8. При разрядке аккумулятор является источником электрической энергии, при этом направление ЭДС Е совпадает с направлением тока I (сплошная стрелка).

Напряжение на зажимах аккумулятора при разрядке определяется из уравнения, составленного для этой цепи по второму закону Кирхгофа: U = R_н·I = E - R₀·I = 2 - 0,01·10 = 1,9 В. Мощность, отдаваемая аккумулятором при разрядке, Р_р = Е·I = 2·10 = 20 Вт.

При зарядке аккумулятор переходит в режим потребителя электроэнергии. При этом ток I аккумулятора направлен встречно ЭДС Е (пунктирная стрелка). Напряжение на зажимах аккумулятора при зарядке в соответствии с уравнением, составленным по второму закону Кирхгофа: U = = E + R₀·I = 2 + 0,01·10 = 2,1 В.

Мощность, потребляемая аккумулятором при его зарядке, Р₃ = Е·I = 2·10 = 20 Вт.

7.1.6. Метод эквивалентных преобразований

Неразветвленная электрическая цепь характеризуется тем, что на всех ее участках протекает один и тот же ток, а разветвленная содержит одну или несколько узловых точек, при этом на участках цепи протекают разные токи.

При расчетах неразветвленных и разветвленных линейных электрических цепей постоянного тока могут быть использованы различные методы, выбор которых зависит от вида электрической цепи.

При расчетах сложных электрических цепей во многих случаях целесообразно производить их упрощение путем свертывания, заменяя отдельные участки цепи с последовательным, параллельным и смешанным соединениями сопротивлений одним эквивалентным сопротивлением с помощью метода эквивалентных преобразований (метода трансфигураций) электрических цепей. Электрическая цепь с последовательным соединением сопротивлений заменяется при этом цепью с одним эквивалентным сопротивлением R_эк, равным сумме всех сопротивлений цепи:

где R₁, R₂, R₃, ... R_n - сопротивления отдельных участков цепи. При этом ток I в электрической цепи сохраняет неизменным свое значение, все сопротивления обтекаются одним и тем же током.

Напряжения (падения напряжения) на сопротивлениях при их последовательном соединении распределяются пропорционально сопротивлениям отдельных участков:

U₁/R₁ = U₂/R₂ = U₃/R₃ = ... = U_n/R_n.

При параллельном соединении сопротивлений все сопротивления находятся под одним и тем же напряжением U.

Электрическую цепь, состоящую из параллельно соединенных сопротивлений, целесообразно заменить цепью с эквивалентным сопротивлением R_эк, которое определяется из выражения

Здесь - сумма величин, обратных сопротивлениям участков параллельных ветвей электрической цепи (сумма проводимостей ветвей цепи); R_k - сопротивление параллельного участка цепи; G_эк - эквивалентная проводимость параллельного участка цепи.

Эквивалентное сопротивление участка цепи, состоящего из одинаковых параллельно соединенных сопротивлений, R_эк = R_k/n, где n - число параллельных ветвей цепи. При параллельном соединении двух сопротивлений R₁ и R₂ эквивалентное сопротивление

R_эк = R₁R₂/(R₁ + R₂),

а токи распределяются обратно пропорционально их сопротивлениям, при этом

U = I₁R₁ = I₂R₂ = I₃R₃ = ... = I_nR_n.

При смешанном соединении сопротивлений, т.е. при наличии участков электрической цепи с последовательным и параллельным соединением сопротивлений, эквивалентное сопротивление цепи определяется в соответствии с выражением

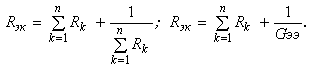
Во многих случаях оказывается целесообразным также преобразование сопротивлений, соединенных треугольником (рис. 7.9), эквивалентной звездой (рис. 7.10).

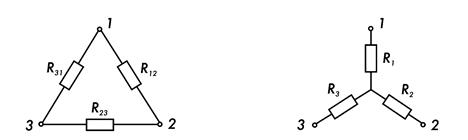
Рис. 7.9. Рис. 7.10.

При этом сопротивления лучей эквивалентной звезды определяют по формулам:

где R₁, R₂, R₃ - сопротивления лучей эквивалентной звезды сопротивлений;

R₁₂, R₂₃, R₃₁ - сопротивления сторон эквивалентного треугольника сопротивлений.

При замене звезды сопротивлений эквивалентным треугольником сопротивлений сопротивления его сторон рассчитывают по формулам:

R₃₁= R₃ + R₁ + R₃R₁/R₂; R₁₂= R₁ + R₂ + R₁R₂/R₃; R₂₃= R₂ + R3₁ + R₂R₃/R₁.

Пример.

Для цепи постоянного тока, приведенной на рис. 7.11, определить общий ток I и токи I₁, I₂, I₃, I₄ в ветвях резисторов R₁ ... R₄. К цепи подведено напряжение U = 240 В, сопротивления резисторов R₁= 20 Ом; R₂= 15 Ом; R₃ = 10 Ом; R₄ = 5 Ом.

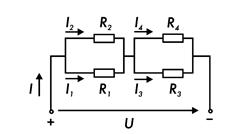
Рис. 7.11.

Решение.

Эквивалентная проводимость участка электрической цепи с резисторами R₁ и R₂:

1/R'_эк= 1/R₁ + 1/R₂= 1/20 + 1/15 = 7/60 Ом^-1,

откуда R'_эк = 60/7 Ом.

Эквивалентная проводимость участка цепи с резисторами R₃ и R₄:

1/R"_эк= 1/R₃ + 1/R₄ = 1/10 + 1/5 = 3/10 Ом^-1,

откуда R"_эк= 10/3 Ом.

Общее сопротивление R = R'_эк + R"_эк = 60/7 + 10/3 = 11,9 Ом.

Общий ток в цепи: I = U/R = 240/11,9 = 20,2 А.

Падения напряжений на параллельных участках цепи:

U₁ = I R'_эк = 20,2×60/7 = 173 В; U₂ = I R''_эк = 20,2×10/3 = 67,3 В;

Токи в ветвях соответствующих резисторов:

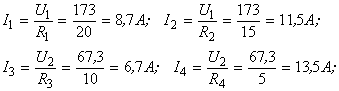
Контрольные вопросы по теме 7.1.

1. Поясните отличие идеального источника напряжения от реального.

2. Чем отличается схема цепи с идеальным источником тока от схемы с реальным источником тока?

3. Три одинаковых сопротивления R включены: 1) последовательно; 2) параллельно. Чему равно суммарное сопротивление участка цепи?

4. Три одинаковых сопротивления R включены «треугольником». Чему равны сопротивления лучей эквивалентной «звезды»?

5. Запишите уравнение второго закона Кирхгофа для цепи, состоящей из реального источника ЭДС (r₀, E) и двух последовательно соединенных сопротивлений R1 и R2.

Задание для самостоятельной работы по теме 7.1.

1. Определить напряжение U зажимах аккумулятора с ЭДС Е = 2 В и внутренним сопротивлением R₀ = 0,01 Ом, мощность, отдаваемую нагрузочному резистору R_Н при разрядке, и мощность, потребляемую аккумулятором при зарядке при токе I = 10А.

2. Для электрической цепи, составленной из параллельно соединенных сопротивлений R₁= 5 Ом, R₂= 10 Ом, R₃= 15 Ом и включенного последовательно с ними сопротивления R₄= 20 Ом определить токи в ветвях I₁, I₂, I₃ и I₄, падения напряжения на сопротивлениях R₁ и R₄ , а также мощности, потребляемые всеми резисторами, если напряжение питания U = 100 В.

3. В электрическую цепь включены четыре резистора: R₁= 5 Ом, R₂= 10 Ом, R₃= 15 Ом и R₄= 20 Ом. Включенные параллельно резисторы R₁и R₄ подсоединены последовательно ко второй паре резисторов R₂и R₃, которые также, в свою очередь, включены параллельно друг другу. Ток через резистор R₃ равен I₃ = 1 А. Найдите токи во всех остальных резисторах и напряжение питания схемы.

7.2. Методы расчета цепей постоянного тока

Изучив вопросы по теме 7.2., вы будете

Знать:

· первый и второй законы Кирхгофа;

· способ расчета цепей методом контурных токов;

· способ расчета цепей методом узловых потенциалов;

· способы расчета нелинейных цепей постоянного тока.

Уметь:

· определять параметры цепи (величину ЭДС, падений напряжений, токов, сопротивлений) с использованием законов Кирхгофа, метода контурных токов и методаузловых потенциалов;

· рассчитывать простейшие нелинейные цепи постоянного тока.

Акцентировать внимание на следующих понятиях:

· алгебраическая сумма токов в узле;

· электрический контур;

· ветвь контура;

· направление обхода контура;

· падение напряжения на участке контура;

· первый закон Кирхгофа;

· второй закон Кирхгофа;

· матричная форма записи уравнений;

· вектрор-столбец токов;

· контурный ток;

· узловой потенциал;

· разность потенциалов;

· нелинейное сопротивление;

· последовательное включение нелинейных и линейных сопротивлений;

· параллельное включение нелинейных и линейных сопротивлений.

7.2.1. Метод применения законов Кирхгофа

В любой электрической цепи в соответствии с первым законом Кирхгофа алгебраическая сумма токов, направленных к узлу разветвления, равна нулю:

где I_k - ток в k-той ветви.

В соответствии со вторым законом Кирхгофа алгебраическая сумма ЭДС в любом замкнутом контуре электрической цепи равна алгебраической сумме напряжений и алгебраической сумме падений напряжений в этом контуре:

где R_i - сопротивление участка цепи рассматриваемого контура;

I_i - ток в цепи сопротивления R_i;

U_j – напряжение на участке цепи.

При расчете электрических цепей методом применения законов Кирхгофа выбирают условные положительные направления токов, ЭДС и напряжений на участках цепи, которые обозначают стрелками на схеме, затем выбирают замкнутые контуры и задаются положительным направлением обхода контуров. При этом для удобства расчетов направление обхода для всех контуров рекомендуется выбирать одинаковым (например, по часовой стрелке). При составлении уравнений по второму закону Кирхгофа для электрических цепей, содержащих источники тока, выбирают замкнутые контуры без источников тока. Для получения независимых уравнений необходимо, чтобы в каждый новый контур входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону Кирхгофа.

Число уравнений, составленных по второму закону Кирхгофа, необходимое для выполнения расчета данной электрической цепи, равно числу неизвестных N.

В большинстве случаев параметры источников ЭДС или напряжения, источников тока, сопротивлений участков электрической цепи известны, при этом число неизвестных равно разности между числом ветвей и числом источников тока N = (N_B - N_Т). Для упрощения расчетов сначала записывают более простые уравнения, составленные по первому закону Кирхгофа, а недостающие - по второму закону Кирхгофа.

Число уравнений, составленных по первому закону Кирхгофа, берется на единицу меньше числа узлов N_у в цепи: N₁ = N_y- 1. При этом токи, направленные к узлу, условно принимаются положительными, а направленные от узла - отрицательными.

Остальное число уравнений N₂ = N - N₁ составляется по второму закону Кирхгофа.

При составлении уравнений по второму закону Кирхгофа ЭДС источников принимаются положительными, если направления их действия совпадают с выбранным направлением обхода контура, независимо от направления тока в них. При несовпадении их записывают со знаком «-». Падения напряжений в ветвях, в которых положительное направление тока совпадает с направлением обхода, независимо от направления ЭДС в этих ветвях - со знаком «+». При несовпадении с направлением обхода падения напряжений записываются со знаком «-».

В результате решения полученной системы из N уравнений находят действительные направления определяемых величин с учетом их знака. При этом величины, имеющие отрицательный знак, в действительности имеют направление, противоположное условно принятому. Направления величин, имеющих положительный знак, совпадают с условно принятым направлением.

Во многих случаях электрические цепи содержат только источники ЭДС и источники напряжения и не имеют источников тока. При этом расчет электрических цепей значительно проще, так как запись уравнений, составленных по второму закону Кирхгофа, упрощается.

Для схемы, изображенной на рис. 7.12, которая содержит два узла (N_y = 2), при числе неизвестных N = 3, подлежащих определению, число уравнений, составленных по первому закону Кирхгофа, N₁ = N_y- 1 = 2 - 1 = 1.

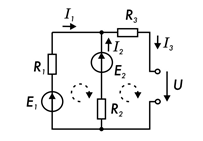
Рис. 7.12.

Число недостающих уравнений, составленных по второму закону Кирхгофа, N₂ = N – N₁ = 3 - 1 = 2. При заданных условных положительных направлениях токов уравнение, составленное по первому закону Кирхгофа для узла 1 электрической цепи с учетом того, что токам, направленным к узлу, приписывается знак «+», а токам, направленным от узла, - знак «-», имеет вид:

I₁ + I₂ - I₃ = 0.

В соответствии с выбранным условным положительным направлением обхода контура, показанным на рис. 7.12 пунктирными стрелками, уравнение, составленное по второму закону Кирхгофа для левого замкнутого контура с учетом положительных направлений токов и ЭДС, записывают в следующем виде:

Е₁ - Е₂ = R₁I₁ - R₂I₂.

Аналогично составляют уравнение по второму закону Кирхгофа для правого замкнутого контура схемы рис. 7.12:

E₂ = R₂I₂ + R₃I₃ + U.

Решение полученной системы трех уравнений позволяет определить неизвестные величины. При этом величины со знаком «+» в действительности имеют направление, совпадающее с соответствующим первоначально заданным на схеме условным направлением. Величины со знаком «-» в действительности имеют направление, противоположное первоначально заданному условному направлению, показанному на схеме рис. 7.12.

Пример.

Для электрической цепи постоянного тока (рис. 7.13) определить токи I₁ … I₃ в ветвях. ЭДС Е₁ = 10 В; Е₂= 20 В; сопротивления резисторов: R₁ = 10 Ом; R₂ = 20 Ом; R₃ = 15 Ом.

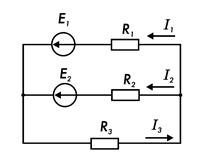
Рис. 7.13.

Решение.

Для узла разветвления в соответствии с принятым на схеме условным положительным направлением составляют уравнение для токов по первому закону Кирхгофа:

I₁ + I₂ = I₃.

Для внешнего и нижнего замкнутых контуров составляют уравнения по второму закону Кирхгофа:

R₁ I₁ + R₃ I₃ = E_1.

R₂·I₂ + R₃·I₃ = E₂.

Запишем полученные уравнения в матричном виде:

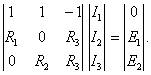
Для решения неоднородных систем линейных уравнений п-го порядка одно из своих первых воплощений нашла идея исключения (алгоритм Гаусса). Он сводится к последовательному исключению неизвестных, в результате чего данная система уравнений преобразуется к эквивалентной системе с верхней треугольной матрицей, решение которой не составляет труда. Это достигается соответствующими операциями над строками расширенной матрицы системы [A, b] размера п × (п + 1). В случае решения системы линейных уравнений электротехники под А понимается матрица сопротивлений, а под b - вектор-столбец ЭДС. В нули преобразуются лишь те элементы матрицы A, которые расположены ниже ее главной диагонали. В результате [А, b] приводится к матрице [U, y], где U - верхняя треугольная матрица с единичными элементами на главной диагонали; у - преобразованный столбец свободных членов.

Запишем расширенную матрицу применительно к условиям решаемой задачи и (посредством деления строк на левый ненулевой элемент матрицы и вычитания строк) проведем преобразования, приводящие матрицу сопротивлений к виду верхней треугольной:

Из последней строки преобразованной матрицы получаем значение тока I₃:

I₃ = 0,615 А.

Подставив это значение во второе уравнение, получаем I₂:

I₂ = 0,538 А.

И, наконец, подставив I₂и I₃в первое уравнение, получаем I₁:

I₂ = 0,077 А.

7.2.2. Метод контурных токов

Для расчета сложных электрических цепей широко используют метод контурных токов, в основу которого положены расчетные (условные) контурные токи, замыкающиеся по смежным контурам разветвленных электрических цепей.

Метод контурных токов позволяет при составлении системы уравнений для расчета электрических цепей не записывать уравнения по первому закону Кирхгофа и тем самым уменьшить общее количество уравнений, необходимых для расчета. Истинные значения токов в ветвях электрической цепи определяются по значениям контурных токов.

В процессе расчета по этому методу определяют независимые замкнутые контуры и задаются условными положительными направлениями контурных токов. При этом во всех замкнутых контурах для упрощения процесса расчета целесообразно задавать контурным токам одинаковые положительные направления. Число уравнений при расчете по методу контурных токов равно числу контурных токов.

При составлении контурных уравнений по второму закону Кирхгофа ЭДС источников питания принимаются положительными, если их направления совпадают с направлениями контурных токов, при несовпадении с контурным током их записывают со знаком «-». Со знаком «-» записывают напряжения, а также падения напряжений, направленные против контурного тока, а со знаком «+», если они совпадают с ним.

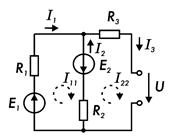
Рис. 7.14.

Величины контурных токов во внешних (не смежных) ветвях оказываются равными по значению токам в ветвях, которые нанесены на электрическую схему. Токи смежных ветвей равны разности контурных токов соседних контуров. При этом со знаком «+» записывается контурный ток, совпадающий с направлением тока в смежной ветви.

Применительно к электрической цепи (рис. 7.14.) в соответствии с заданным направлением ЭДС, напряжения, токов в ветвях и контурных токов уравнения, составленные по второму закону Кирхгофа для замкнутых контуров, записывают в следующем виде:

E₁ + E₂ = (R₁ + R₂) I₁₁ – R₂ I₂₂;

-E₂ = (R₂ + R₃) I₂₂ – R₂ I₁₁ + U.

В результате решения полученной системы уравнений и определяют контурные токи I₁₁ и I₂₂.

При этом токи во внешних (несмежных) ветвях электрической цепи оказываются численно равными соответствующим контурным токам: I₁ = I₁₁; I₃ = I₂₂. Ток в смежной ветви определяют из уравнения, составленного по первому закону Кирхгофа для точки разветвления электрической цепи: I₁ - I₂ - I₃ = 0, откуда I₂ = I₁ - I₃ = I₁₁ - I₂₂.

Пример.

Для электрической цепи постоянного тока (рис. 7.13) определить токи I₁ … I₃ в ветвях. Для удобства расчетов изменим положение ветвей так, как это изображено на рис. 7.15

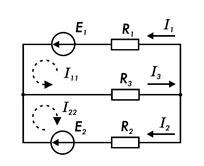
Рис. 7.15.

Решение.

Запишем уравнения контурных токов I₁₁ и I₂₂:

(R₁ + R₃) I₁₁ + R₃ I₂₂ = E₁;

R₃ I₁₁ + (R₂ + R₃) I₂₂ = E₁.

В матричной форме эти уравнения имеют следующий вид:

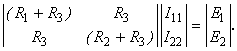
Применим алгоритм Гаусса для решения системы уравнений:

Из последнего уравнения I₂₂ = 0,538 А.

Подставим это значение в первое уравнения, тогда I₁₁ = 0,077 А.

Ток I₃ определим как сумму токов I₁₁ и I₂₂:

I₃ = I₁₁ + I₂₂ = 0,615 А.

7.2.3. Метод узлового напряжения (узловых потенциалов)

Метод узлового напряжения целесообразно использовать для расчета электрических цепей, содержащих несколько параллельных ветвей, присоединенных к паре узлов. Преимущество этого метода перед другими возрастает с увеличением числа параллельных ветвей электрических цепей. При этом определяется узловое напряжение, что позволяет достаточно просто определять токи в параллельных ветвях и другие величины, характеризующие подобные электрические цепи.

Узловое напряжение между двумя точками разветвлений (узлами) определяют в соответствии с выражением

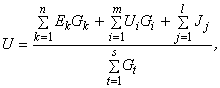
где - алгебраическая сумма произведений ЭДС и проводимостей соответствующих ветвей;

- алгебраическая сумма произведений напряжений и проводимостей соответствующих ветвей;

- алгебраическая сумма токов источников тока в ветвях;

G_k = 1/R_k- проводимость k-той ветви цепи, равная величине, обратной ее сопротивлению;

- сумма проводимостей всех ветвей.

При расчете электрических цепей по методу узлового напряжения задаются условным положительным направлением указанного напряжения, рассчитывая его по соответствующей формуле. Определяют проводимости всех ветвей. При определении токов в параллельных ветвях для соответствующих замкнутых контуров выбирают направления обхода контура и составляют уравнения по второму закону Кирхгофа. ЭДС, напряжения и токи источников тока принимаются положительными, если они направлены по направлению обхода контура, и отрицательными, если они направлены против направления его обхода.

При отсутствии в электрической цепи источников тока процесс расчета существенно упрощается. При этом выражение для определения напряжения, действующего между двумя узлами, приводится к виду

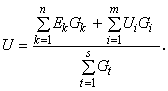
Рассмотрим применение метода узлового напряжения на примере схемы, изображенной на рис. 7.16, а. При заданном условном положительном направлении напряжения U₁₂, действующего между узлами 1 и 2, ЭДС в замкнутом контуре, образованном из соответствующей ветви и замыкающего напряжения U_n, при обходе контура по заданному положительному направлению принимается со знаком «+», если совпадает с направлением обхода, а если не совпадает - со знаком «-».

Напряжения, не совпадающие при обходе соответствующего контура с направлением напряжения между узлами U₁₂, принимаются со знаком «-», а совпадающие - со знаком «+».

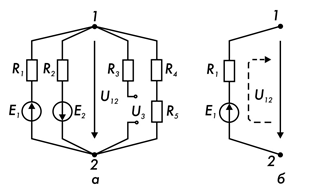
Рис. 7.16.

Знаки в расчетной формуле не зависят от направления токов в ветвях электрической цепи. С учетом этого выражение для напряжений между узлами 1 и 2 цепи записываем в следующем виде:

Для расчета токов в ветвях электрической цепи составляют замкнутый контур, состоящий из рассматриваемой ветви цепи, замыкаемой напряжением U₁₂ между узлами, с учетом действительного его направления. Расчетная схема ветви с резистором R₁ и ЭДС Е₁приведена на рис. 7.16, б. Задавшись условным положительным направлением обхода полученного таким образом контура, например, по часовой стрелке (направление обхода показано пунктирной стрелкой), записывают с учетом знаков уравнение, составленное по второму закону Кирхгофа; Е₁ = R₁·I₁ + U₁₂, отсюда определяется величина тока I₁ в данной ветви цепи. Аналогичным образом определяются токи в других ветвях электрической цепи.

Пример.

Для электрической цепи постоянного тока (рис. 7.15) определить величину токов в ветвях цепи, воспользовавшись методом узловых потенциалов. Напомним, что Е₁ = 10 В; Е₂= 20 В; сопротивления резисторов: R₁ = 10 Ом; R₂ = 20 Ом; R₃ = 15 Ом.

Решение. Запишем формулу для вычисления напряжения между узлами 1 и 2 цепи:

Тогда токи в ветвях оказываются равными:

I₁ = (E₁ – U₁₂)/R₁ = 0,77/10 = 0,077 A.

I₂ = (E₂ – U₁₂)/R₂ = 10,77/20 = 0,538 A.

I₃ = U₁₂/R₃ = 9,23/15 = 0,615 A.

Нетрудно убедиться в том, что результат идентичен полученному ранее (методом уравнений Кирхгофа или методом контурных токов).

7.2.4. Основные сведения о нелинейных электрических цепях постоянного тока

К нелинейным электрическим цепям постоянного тока относятся электрические цепи, содержащие нелинейные сопротивления, обладающие нелинейными вольтамперными характеристиками I(U), т. е. нелинейной зависимостью тока от приложенного к нелинейному сопротивлению напряжения.

Различают неуправляемые нелинейные сопротивления (лампы накаливания, газотроны, бареттеры, полупроводниковые диоды и т. д.), которые характеризуются одной вольтамперной характеристикой, и управляемые (многоэлектродные лампы, транзисторы, тиристоры и др.), которые характеризуются семейством вольтамперных характеристик.

Расчет нелинейных электрических цепей постоянного тока обычно осуществляют графоаналитическим методом. При этом можно использовать и аналитический метод расчета, который, однако, достаточно сложен. Для выполнения расчета нелинейных электрических цепей должна быть известна вольтамперная характеристика соответствующего нелинейного сопротивления, представленная в виде графика или таблицы.

При расчете электрических цепей с последовательным включением нелинейных (или линейных и нелинейных) сопротивлений R₁ и R₂(рис. 7.17) вольтамперные характеристики соответствующих сопротивлений I₁(U) и I₂(U) представляются в общей координатной системе и по ним строится общая вольтамперная характеристика I(U) всей нелинейной электрической цепи (рис. 7.18), абсцисса каждой из точек которой при заданном токе I (заданной ординате) находится как сумма соответствующих падений напряжения (U = U₁ + U₂) на этих сопротивлениях R₁ и R₂, поскольку при последовательном соединении по сопротивлениям протекает один и тот же ток I цепи. Таким образом, по общей вольтамперной характеристике I(U) нелинейной цепи при заданном значении напряжения U и последовательном соединении сопротивлений легко определяют ток I в нелинейной цепи, а по заданному току I находят напряжение U, подводимое к нелинейной цепи, и напряжения U₁ и U₂ на каждом из последовательно соединенных сопротивлений.

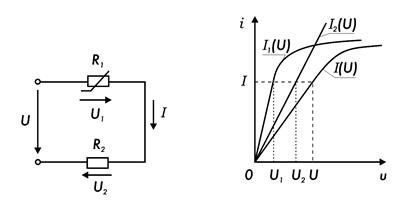
Рис. 7.17. Рис. 7.18.

При параллельном соединении нелинейных (или линейных и нелинейных) сопротивлений R₁ и R₂ (рис. 7.19) также строят общую вольтамперную характеристику I(U) нелинейной электрической цепи (рис. 7.20). При этом ординату каждой из точек общей вольтамперной характеристики при заданном подводимом к цепи напряжении U (заданной абсциссе) определяют как сумму токов в цепях соответствующих сопротивлений (I = I₁+ I₂), так как при параллельном соединении на всех сопротивлениях действует одно и то же напряжение U. Следовательно, при параллельном включении сопротивлений по общей вольтамперной характеристике I(U) и заданном значении напряжения U нетрудно определить и ток I в нелинейной электрической цепи. При заданном общем токе I также легко определить и напряжение U, подводимое к данной нелинейной электрической цепи, и токи I₁ и I₂, протекающие в цепи каждого из параллельно соединенных сопротивлений.

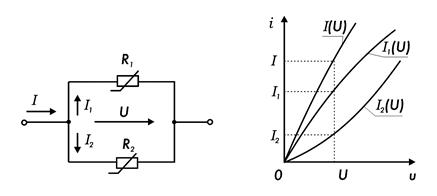
Рис. 7.19. Рис. 7.20.

Следует отметить, что изложенная методика расчета нелинейных электрических цепей при последовательном и параллельном соединении сопротивлений справедлива для любого числа сопротивлений, включенных в цепь последовательно или параллельно.

При расчете нелинейных электрических цепей со смешанным (последовательно-параллельным) соединением нелинейных (или линейных и нелинейных) сопротивлений (рис. 7.21) строят вольтамперную характеристику I(U₁) параллельного участка цепи.

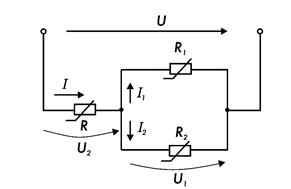
Рис. 7.21.

При этом образуется нелинейная электрическая цепь с последовательным соединением сопротивлений, для которой строится общая вольтамперная характеристика I(U) с учетом того, что подводимое к цепи напряжение U при данном токе цепи I равно сумме напряжений на параллельном U₁ и на последовательном U₂ участках цепи (U = U₁ + U₂).

Контрольные вопросы по теме 7.2.

1. В чем отличие контурного тока от тока в ветви контура?

2. Что означает, если в результате расчетов значение тока оказывается отрицательным?

3. Сколько уравнений по первому и второму законам Кирхгофа следует составить для схемы, состоящей из четырех параллельных ветвей?

4. В каких случаях метод узловых потенциалов является более экономичным по сравнению с методом контурных токов и методом законов Кирхгофа?

5. Чем объясняется отклонение от линейности в вольт-амперной характеристике лампы накаливания? Полупроводникового диода?

Задание для самостоятельной работы по теме 7.2.

1. Два источника постоянного тока с ЭДС Е₁ = Е₂ = 115 В и внутренними сопротивлениями R₀₁ = 0,2 Ом и R₀₂ = 0,4 Ом включены параллельно на нагрузку R_Н = 5 Ом. Определить токи во всех ветвях электрической цепи.

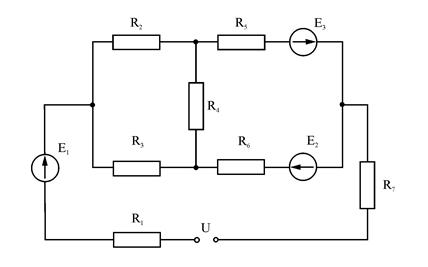
2. Электрическая цепь постоянного тока содержит источник питания: Е₁ = 50 В, Е₂ = 20 В и Е₃ = 45 В. Сопротивления, включенные в цепь, имеют номиналы: R₁ = 10 Ом, R₂ = 30 Ом, R₃ = 50 Ом, R₄= 20 Ом, R₅ = 1 Ом, R₆ = 20 Ом, R₇ = 10 Ом. Напряжение, приложенное к цепи, U = 80 В. Внутренними сопротивлениями источников пренебречь. Определить токи I₁ – I₆в ветвях цепи, а также напряжение между токами 1 и 4 цепи. Определить величину падений напряжения на всех сопротивлениях цепи.

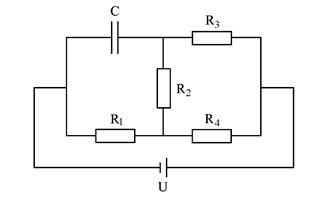
3. В электрической цепи постоянного тока, представленной на рисунке, напряжение U = 24 В, сопротивления R₁ = 5 Ом, R₂ = 10 Ом, R₁ = 15 Ом, R₁ = 25 Ом. Найдите напряжение на обкладках конденсатора С.