Тема №6. Дифференцирование функций.

 

Производная логарифмической функции

На предыдущем занятии по четырехступенчатому правилу нами была найдена производная логарифмической функции

 

 (71)

в частности, при а = е мы получили

. (72)

 

Рассмотрим сложную функцию , удовлетворяющую всем условиям существования производной сложной функции.

Как будет выглядеть производная функции ?

Последнюю функцию нужно рассматривать как сложную функцию , где .

По теореме о производной сложной функции имеем:

 

.

 

Таким образом, нами найдена производная сложной функции :

 

 (73)

Отсюда, в частности, при а = е получим:

. (74)

 

Производная показательной функции

Рассмотрим показательную функцию

 (75)

 

Найдем производную функции (75), воспользовавшись производной логарифмической функции.

Прологарифмируем обе части равенства  по основанию :

 

. (76)

 

Возьмем от обеих частей равенства (76) производную по х, рассматривая левую часть этого равенства как сложную
функцию от х:

 

.

 

Подставляя вместо  его выражение , получим

 

. (77)

Отсюда в частности при  имеем:

. (78)

 

Рассмотрим сложную функцию которая удовлетворяет условиям существования сложной функции:

 

.

 

По теореме о производной сложной функции имеем:

 

.

Окончательно имеем:

. (79)

В частности, при а = е получим

. (80)

 

Производная степенной функции

,

где a – произвольное действительное число.

Прологарифмируем обе части равенства  по основанию :

 

или

. (81)

 

Возьмем от обеих частей равенства (81) производную по х, воспользовавшись формулами (72) и (73):

 

.

 

Подставим в последнем равенстве вместо у(х) степенную функцию :

 

.

Окончательно получим:

. (82)

 

В случае задания сложной степенной функции  по аналогии с вышеизложенным получим:

 

,

или

.(83)

 

Отсюда, в частности, при  получим:

 

 

или окончательно

. (84)

Отсюда при n = 2 получим:

. (85)

 

Производная показательно-степенной функции

Рассмотрим функцию , заданную на множестве Х, где выполняются условия существования производной сложной функции: функции  дифференцируемы, функция у дифференцируема по u и v.

Для отыскания искомой производной возьмем от обеих частей равенства  натуральный логарифм:

 

. (86)

 

Возьмем от обеих частей равенства (86) производную по х, воспользовавшись формулой (73) и производной произведения:

 

,

 

 

 (87)

 

Подставляя в равенстве (87) вместо  показательно-степенную функцию , получим:

 

 

или окончательно

 

. (88)

 

Из формулы (88) следует, что производная показательно-степенной функции равна сумме производных от функции , которая вначале рассматривается как показательная функция, а затем как степенная.

 

 

Производные тригонометрических функций

 

1. .

На предыдущем занятии (занятие 5) нами была найдена производная  по четырехступенчатому правилу, и было установлено, что

. (89)

 

Если дана сложная функция , то по формуле производной сложной функции получим:

 

 (90)

 

2.  хÎ(–¥;+¥).

Найдем у^’, воспользовавшись формулами приведения и формулой (89).

Имеем:

,

 

где за u принята разность : .

Отсюда находим:

 

Таким образом,

. (91)

 

По аналогии в случае задания сложной функции  будем иметь:

 

.

 

3.

 

Для отыскания производной воспользуемся формулой для производной дроби:

 

.

 

Таким образом,

 

. (92)

 

В случае задания сложной функции по аналогии получим:

 

. (93)

 

4. .

Для отыскания производной  воспользуемся формулой приведения и формулой (93) для производной :

 

.

 

 

Таким образом, имеем:

. (94)

 

В случае задания сложной функции будем иметь:

 . (95)

 

Производные обратных тригонометрических функций

1. .

Так как функция  на заданном отрезке монотонна и непрерывна, то по теореме о существовании обратной функции функция  имеет обратную . Так как производная обратной функции отлична от нуля , то по теореме о производной обратной функции имеем:

 

. (96)

 

Здесь мы воспользовались основным тригонометрическим тождеством .

Отсюда находим, что . Знак перед радикалом в равенстве (96) взят со знаком «плюс», т.к.  на интервале  является величиной положительной. Подставляя вместо у(x) обратную тригонометрическую функцию

arcsin x, получим:

. (97)

 

 В случае задания сложной функции  получим:

 

. (98)

2. , .

На интервале (–1; 1) функция  монотонна и непрерывна. По теореме о существовании обратной функции функция  имеет обратную функцию , которая на интервале  по переменной у имеет производную, отличную от нуля. Следовательно, по теореме о производной обратной функции имеем:

 

 

или

 

 (99)

 

По тем же соображениям перед радикалом взят знак «плюс», т.к. функция  на интервале  положительна.

В случае задания сложной функции по аналогии получим:

 (100)

3. , .

Функция  на заданном интервале монотонна и непрерывна, следовательно, на соответствующем интервале  определена однозначная обратная функция . Заметим, что производная функции  отлична от нуля. Тогда по теореме о производной обратной функции

 

 или . (101)

 

В случае заданной сложной функции  получим:

 

. (102)

4.  

Функция  на интервале  монотонна и непрерывна. По теореме о существовании обратной функции заданная функция имеет обратную , которая на интервале  также монотонна и непрерывна. Заметим, что  при . Тогда по теореме о производной обратной функции имеем:

 

,

 или

. (103)

 

В случае заданной сложной функции

по аналогии будем иметь:

. (104)

Параметрическое задание функции

Одним из способов аналитического задания функции является параметрический способ.

 

В качестве примера рассмотрим окружность в прямоугольной системе координат Оху (рис. 6.1).

Пусть М (х; у) – произвольная точка окружности; çОМç= R – радиус окружности.

 

 

 

 

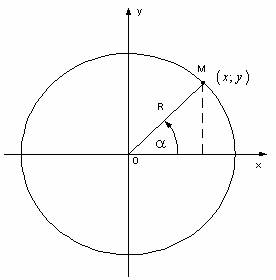
По определению тригонометрических функций  и  имеем:

 

, (105)

где .

 

Равенствами (105) зависимость функции у от х задается через угол a, который является параметром.

Легко заметить, что из равенства (105) следует:

 

,

 

что является известным каноническим уравнением

окружности.

В общем случае функция у от переменной х называется заданной параметрически, если эта зависимость задается системой равенств (рис. 106):

 (106)

где .

 

Найдем производную от функции, заданной параметрически равенствами (106). Пусть  удовлетворяет всем условия дифференцируемости и существования обратной функции , где : функция  монотонна и непрерывна на отрезке , существует конечный предел , отличный от нуля.

Переменную у можно рассматривать как сложную функцию переменной х на отрезке :

.

 

По теореме о производной сложной функции имеем:

 

 (107)

Так как производная обратной функции  равна обратной величине производной прямой функции, т.е. , то равенство (107) можно переписать так:

 

 или  . (108)

 

Пример. Функция  переменной х задана параметрически

 

 где .

Требуется найти . По формуле (108) имеем:

 

 

Найдем производную второго порядка от функции, заданной параметрически.

 

Функция  является сложной функцией переменной х.

 

По теореме о производной сложной функции имеем:

 

 

 

или окончательно

  . (109)

 

Дифференцирование неявной функции

Пусть уравнение

 (110)

на множестве Х задает неявную функцию . Общая формула для отыскания производной неявной функции задается в разделе функций многих переменных. Однако если в уравнении (110) рассматривать переменную y как функцию переменной х, то, взяв производную по х от обеих частей равенства (110), можно найти искомую производную как функцию переменных х и у.

Действительно, уравнение:

. (111)

 

на множестве  определяет неявную функцию .

Возьмем от обеих частей уравнения (111) производную по х:

 

 . (112)

 

Решая уравнение (112) относительно , находим:

.

 

На основе найденных производных основных элементарных функций составим таблицу производных. В нижеприведенную таблицу включены также основные правила дифференцирования.

 

Таблица производных

 

 

Рассмотрим примеры на отыскание производных заданных функций по таблице производных и основным правилам взятия производных дифференцируемых функций.

 

Пример 1. Найти производную функции

у = 2х⁴ + 4х³ +3х² +5х –2.

 

На основании правил дифференцирования и формулы производной степенной функции имеем:

 

y'=(2х⁴ + 4х³ +3х² +5х –2)' = (2x⁴)' + (4x³)' + (3x²)' + (5x)' – (2)' =
= 2(x⁴)' + 4(x³)' + 3(x²)' + 5(x)' – 0 = 2 × 4x³ + 4 × 3x² + 3 × 2x + 5 =
= 8x³ +12x² +6x + 5.

 

Пример 2. Найти производную функции

.

Имеем:

 

Пример 3. Дана функция f(x) = x³– 4x – 1.

Вычислить  (–2),  (–1),  (0),  (1),  (3).

1.     Находим сначала производную заданной функции:

 

 (х) = 3х² – 4.

 

1.     Подставляем в выражение первой производной вместо х последовательно числа –2; –1; 0; 1; 3:

 

 (–2) = 3 × (–2)² – 4 = 8;

 

 (–1) = 3 × (–1)² – 4 = –1;

 

 (0) = 3 × 0 – 4 = –4;

 

 (1) = 3 × 1² – 4 = –1;

 

 (3) = 3 × 3² – 4 = 23.

 

Пример 4. Найти производную функции у = х² sinx – x × cosx.

Производную находим по правилу производной от алгебраической суммы и по формуле производной от произведения дифференцируемых функций.

Имеем:

 

Пример 5. Найти производную функции .

Искомую производную найдем по формуле производной от дроби:

 

 

 

Пример 6. Найти производную сложных функций:

 

1. Если предположить, что 4х = u, то функцию у = cos 4х можно рассматривать как сложную функцию:

y = cos u, u = 4x.

По правилу нахождения производной сложной функции имеем:

При взятии производных сложных функций в дальнейшем мы будем пользоваться соответствующими формулами взятия производных от сложных функций.

 

2. _.

 

3.

 

4.

 

5.

 

6.

 

7. .

 

8.

 

Пример 7. Найти производную от функции, заданной неявно:

ху + sinу = 0.

 

Чтобы найти производную  от неявной функции нужно продифференцировать по х обе части заданного равенства, рассматривая переменную у как функцию от х, найти  из полученного равенства.

Имеем:

 

Окончательно находим: