7. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
7.1. МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ
7.1.1. Постановка задачи. Основные понятия
Пусть функция ![]() определена на
определена на ![]() .
Задачей одномерной оптимизации будем называть задачу, в которой требуется найти
.
Задачей одномерной оптимизации будем называть задачу, в которой требуется найти
![]() ,
,
![]() .
.
Решением или точкой
максимума (минимума) этой задачи назовем такую точку ![]() ,
что
,
что 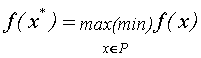 .
.
Методы одномерной оптимизации условно подразделяются
на три группы. К первой группе относятся методы, основанные лишь на вычислении
значений самой функции ![]() (методы нулевого порядка).
Вторую группу составляют методы, использующие значения как самой функции. Так и
ее первой производной (методы первого порядка). И, наконец, к третьей
группе относятся методы, использующие значения функции, ее первой и второй
производной (методы второго порядка).
(методы нулевого порядка).
Вторую группу составляют методы, использующие значения как самой функции. Так и
ее первой производной (методы первого порядка). И, наконец, к третьей
группе относятся методы, использующие значения функции, ее первой и второй
производной (методы второго порядка).
В дальнейшем будем считать, что максимизируемая функция является унимодальной.
Определение. Функция ![]() называется унимодальной на множестве
называется унимодальной на множестве ![]() , если
существует единственная точка
, если
существует единственная точка ![]() ее максимума на
ее максимума на ![]() и
и
![]() ,
если
,
если ![]() и
и
![]() ,если
,если
![]() для любых
для любых ![]() .
.
Другими словами, унимодальная функция монотонно возрастает слева от точки максимума и монотонно убывает справа от нее.
Отметим, что
предположение об унимодальности функции в окрестностях точки ![]() весьма естественно, поэтому получение
информации о таком промежутке является важным этапом процедуры оптимизации.
Обычно в процессе применения методов одномерной оптимизации можно выделить два
этапа: поиск отрезка, содержащего точку максимума, уменьшение длины этого отрезка
до заранее установленной величины (уточнение координаты точки максимума на
данном отрезке).
весьма естественно, поэтому получение
информации о таком промежутке является важным этапом процедуры оптимизации.
Обычно в процессе применения методов одномерной оптимизации можно выделить два
этапа: поиск отрезка, содержащего точку максимума, уменьшение длины этого отрезка
до заранее установленной величины (уточнение координаты точки максимума на
данном отрезке).
В разделе данной главы
1.2 рассмотрен алгоритм I этапа – поиск границ отрезка, содержащего точку максимума унимодальной
функции ![]() , далее излагаются методы II этапа – отыскивания точки максимума на заданном
отрезке.
, далее излагаются методы II этапа – отыскивания точки максимума на заданном
отрезке.
7.1.2. Поиск отрезка, содержащего точку максимума. Алгоритм Свенна
Исходные
данные: ![]() - начальная точка,
- начальная точка, ![]() – шаг поиска
– шаг поиска ![]() .
.
Вычислить
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Если
![]() , то
, то ![]() ,
перейти к шагу 4.
,
перейти к шагу 4.
Если
![]() , то
, то ![]() ,
, ![]() , перейти к шагу 4, в противном случае
, перейти к шагу 4, в противном случае ![]()
![]() ;
; ![]() ,
конец.
,
конец.
![]() , вычислить
, вычислить ![]() .
.
Если
![]() , то
, то ![]() ,
перейти к шагу 4.
,
перейти к шагу 4.
Если
![]() , то
, то ![]() ;
; ![]() , конец, в противном случае
, конец, в противном случае ![]() ;
; ![]() , конец.
, конец.
Заметим,
что случай ![]() (шаг 3) не рассматривается, так как
он противоречит предположению об унимодальности функции
(шаг 3) не рассматривается, так как
он противоречит предположению об унимодальности функции ![]() .
.
Пример
1. ![]() ;
; ![]() ;
; ![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
Поскольку
![]() ,
, ![]() ,
,![]() .
.
Далее
![]() .
.
![]() ,
, ![]() ,
,![]() .
.
![]() ,
, ![]() ,
,![]() .
.
![]() ,
, ![]() ,
,![]() .
.
![]() ,
, ![]() ,
,![]() ;
; ![]() .
.
Уменьшение длины отрезка, содержащего точку максимума, достигается путем последовательного исключения частей этого отрезка. Величина интервала, исключаемого на каждом шаге, зависит от расположения двух пробных точек внутри отрезка. Поскольку координата точки максимума априори неизвестна, целесообразно размещать пробные точки таким образом, чтобы обеспечивать уменьшение длины отрезка в одном и том же отношении.
7.1.3. Дихотомический поиск (метод деления отрезка пополам)
Пробные точки y, z на каждом шаге этого метода выбираются следующим образом:
![]() ,
, ![]() ,
где
,
где ![]() - параметр метода,
- параметр метода, ![]() .
.
При
малых ![]() каждая из пробных точек делит отрезок
каждая из пробных точек делит отрезок ![]() почти пополам, т.е. исключению будет
подлежать почти половина отрезка.
почти пополам, т.е. исключению будет
подлежать почти половина отрезка.
Алгоритм
Исходные данные. Отрезок ![]() , содержащий точку максимума;
параметр
, содержащий точку максимума;
параметр ![]() и параметр
окончания счета
и параметр
окончания счета ![]()
![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
Если ![]() , то
, то ![]() ,
конец.
,
конец.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Если ![]() , то
, то ![]() ,
, ![]() , в противном случае
, в противном случае ![]() ,
, ![]() .
.
![]() , перейти к шагу 2.
, перейти к шагу 2.
Пример 2. Найти точку
максимума функции ![]() на отрезке
на отрезке ![]() ;
; ![]() ;
; ![]() .
.
Итерация 1.
![]() ,
,
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ,
,
![]() ;
; ![]() .
.
Итерация 2.
![]() ,
,
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ,
,
![]() ;
; ![]() .
.
Итерация 3.
![]() ,
,
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ,
,
![]() ;
; ![]() .
.
Итерация 4.
![]() ;
;
![]() .
.
Таким образом, на каждой
итерации дихотомического поиска производится два вычисления значения функции и
после n
вычислений (n/2 итераций), длина начального интервала уменьшается
приблизительно в ![]() раз.
раз.
7.1.4. Метод золотого сечения
Как
известно, золотым сечением отрезка называется деление отрезка на две неравные
части так, чтобы отношение длины всего отрезка к длине большей части равнялось
отношению длины большей части к длине меньшей части отрезка. Легко показать,
что золотое сечение отрезка ![]() производится двумя
точками y и z, симметричными
относительно середины отрезка.
производится двумя
точками y и z, симметричными
относительно середины отрезка.
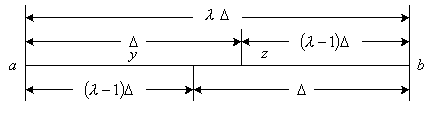
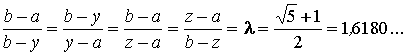
Отсюда
![]()
![]()
Нетрудно также проверить,
что точка y
производит золотое сечение отрезка ![]() , а точка z производит золотое сечение отрезка
, а точка z производит золотое сечение отрезка ![]() . На этом свойстве, позволяющем на каждой
итерации вычислить значение функции лишь в одной пробной точке, и основан
алгоритм золотого сечения.
. На этом свойстве, позволяющем на каждой
итерации вычислить значение функции лишь в одной пробной точке, и основан
алгоритм золотого сечения.
Исходные данные. ![]() -
отрезок, содержащий точку максимума,
-
отрезок, содержащий точку максимума, ![]() - параметр окончания
счета.
- параметр окончания
счета.
![]() ;
; ![]() ,
, ![]() ,
, ![]() .
. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Если ![]() , то перейти к шагу 4.
, то перейти к шагу 4.
![]() ,
, ![]() ;
; ![]() ;
; ![]() .
. ![]() ;
; ![]() ,
перейти к шагу 5.
,
перейти к шагу 5.
![]() ,
, ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Если ![]() , то
, то ![]() ,
конец.
,
конец.
![]() , перейти к шагу 2.
, перейти к шагу 2.
Пример 3. Найти точку
максимума функции ![]() на отрезке
на отрезке ![]() ;
; ![]() .
.
![]() ;
;
![]() ,
, ![]() .
.
![]() .
.
![]() .
.
![]() ;
;
![]() .
.
Итерация 1.
Так как ![]() , то
, то ![]() ,
, ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Итерация 2.
Так как ![]() , то
, то ![]() ,
, ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Итерация 3.
Так как ![]() , то
, то ![]() ,
, ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() .
.
Итерация 4.
Так как ![]() , то
, то ![]() ,
, ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ,
следовательно,
,
следовательно, ![]() .
.
Как было отмечено, выше
на каждой итерации метода золотого сечения производится лишь одно вычисление
значения функции. При этом длина полученного в результате одной итерации
отрезка состоит ![]() , где
, где ![]() -
длина исходного интервала.
-
длина исходного интервала.
Если сравнить методы дихотомического поиска и золотого сечения, используя в качестве критерия эффективности, то

т.е. метод золотого сечения оказывается более эффективным.
7.1.5. Метод ДСК-Пауэлла
Основная идея метода связана с возможностью аппроксимации непрерывной унимодальной функции полиномом и использованием аппроксимирующего полинома для оценивания координаты точки максимума.
Простейшим вариантом полиномиальной интерполяции
является квадратная аппроксимация. Если в точках ![]() ,
, ![]() ,
, ![]() известны
соответствующие значения функции
известны
соответствующие значения функции ![]() , то можно построить
интерполяционный полином второй степени:
, то можно построить
интерполяционный полином второй степени:
![]() ,
где
,
где
![]() ;
;
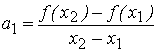 ;
;
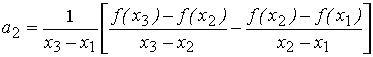 .
.
Стационарная точка ![]() этого
полинома определяется уравнением
этого
полинома определяется уравнением ![]() , откуда
, откуда 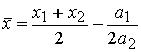 .
.
Метод ДСК-Пауэлла включает в
качестве начального этапа поиск отрезка, содержащего точку максимума (алгоритм
Дэвиса, Свенна и Кэмпи), после чего проводится квадратичная аппроксимация до
тех пор, пока с требуемой точностью не будет найдена координата точки максимума
функции ![]() (алгоритм Пауэлла).
(алгоритм Пауэлла).
Исходные данные. ![]() - начальная точка,
- начальная точка, ![]() - шаг поиска,
- шаг поиска, ![]() -
параметр окончания счета.
-
параметр окончания счета.
Вычислить ![]() ,
,![]() ,
, ![]() .
.
Если ![]() , то
, то ![]() .
.
![]() ,
вычислить
,
вычислить ![]() .
.
![]() ;
;
![]() , вычислить
, вычислить ![]() .
.
Если ![]() , то
, то ![]() и
перейти к шагу 4. В противном случае
и
перейти к шагу 4. В противном случае ![]() ;
; ![]() ;
; ![]() ;
; ![]() , вычислить
, вычислить ![]() .
.
Если ![]() , то перейти к шагу 7. В противном случае
, то перейти к шагу 7. В противном случае
![]() ;
; ![]() ;
; ![]() .
.
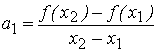 ;
;
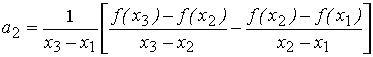 ;
; 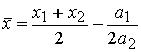 .
.
Если выполнено одно (или оба) из условий
![]() ,
,
![]() ,
то
,
то ![]() , то конец.
, то конец.
Если ![]() , то
, то ![]() ,
, ![]() , перейти к шагу 6. В противном случае
, перейти к шагу 6. В противном случае ![]() ,
, ![]() ,
, ![]() , перейти к шагу 6.
, перейти к шагу 6.
Пример 4. Найти точку
максимума функции ![]() ,
, ![]() ;
;![]() ;
; ![]() .
.
![]() ;
;
![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
Так как ![]() , то
, то ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
![]() .
.
Итерация 1.
Так как ![]() , то квадратичная интерполяция будет
проводиться по точкам
, то квадратичная интерполяция будет
проводиться по точкам ![]() ;
; ![]() ;
; ![]() .
.
Коэффициенты интерполяционного полинома:
![]() ;
;
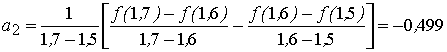 ,
,
а точка максимума: ![]() ;
;
![]() .
.
![]() ,
,
![]() ;
; ![]() ;
; ![]() .
.
Итерация 2.
Так как ![]() , то квадратичная интерполяция будет
проводиться по точкам
, то квадратичная интерполяция будет
проводиться по точкам ![]() ;
; ![]() ;
; ![]() .
.
Коэффициенты интерполяционного полинома:
![]() ;
;
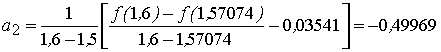 ,
,
а точка максимума: ![]() ;
;
![]() .
.
![]() ,
следовательно,
,
следовательно, ![]() .
.
7.1.6. Метод средней точки
Для отыскивания корня
уравнения ![]() которому удовлетворяет точка максимума
унимодальной и дифференцируемой на заданном отрезке функции
которому удовлетворяет точка максимума
унимодальной и дифференцируемой на заданном отрезке функции ![]() , будем пользоваться алгоритмом
исключения интервалов, на каждой итерации которого рассматривается лишь одна
точка
, будем пользоваться алгоритмом
исключения интервалов, на каждой итерации которого рассматривается лишь одна
точка ![]() .
.
Если в точке ![]() выполняется условие
выполняется условие ![]() то с учетом предположения об
унимодальности можно утверждать, что точка максимума не может находиться левее
точки
то с учетом предположения об
унимодальности можно утверждать, что точка максимума не может находиться левее
точки ![]() , следовательно, интервал
, следовательно, интервал ![]() может быть исключен. С другой стороны,
если
может быть исключен. С другой стороны,
если ![]() то точка максимума не может находиться
правее точки
то точка максимума не может находиться
правее точки ![]() , т.е. исключению подлежит интервал
, т.е. исключению подлежит интервал ![]() . На этих рассуждениях и основан метод
средней точки (поиск Больцано).
. На этих рассуждениях и основан метод
средней точки (поиск Больцано).
Алгоритм метода средней точки
Исходные данные. Точка ![]() и
и ![]() такие, что
такие, что ![]() ,
, ![]() ,
, ![]() -
параметр окончания счета.
-
параметр окончания счета.
![]() .
Вычислить
.
Вычислить ![]() .
.
Если ![]() , то
, то ![]() ,
конец.
,
конец.
Если ![]() , то
, то ![]() ,
перейти к шагу 1. в противном случае
,
перейти к шагу 1. в противном случае ![]() , перейти к шагу 1.
, перейти к шагу 1.
Пример 1.5. Найти точку
максимума функции ![]() на отрезке
на отрезке ![]() ;
; ![]() .
.
![]() .
.
Итерация 1.
![]() ;
;
![]() ,
, ![]() .
.
Итерация 2.
![]() ;
;
![]() ,
, ![]() .
.
Итерация 3.
![]() ;
;
![]() ,
, ![]() .
.
Итерация 4.
![]() ;
;
![]() ,
, ![]() .
.
Итерация 5.
![]() ;
;
![]() ,
, ![]() .
.
Итерация 6.
![]() ;
;
![]() ,
, ![]() .
.
Итерация 7
![]() ;
;
![]() ;
;
![]() ,
,
![]() .
.
7.1.7. Метод хорд (секущих)
При реализации этого метода учитывается не только знак
производной, но и ее значение. Метод заключается в решении уравнения ![]() метод хорд и носит потому то же
название.
метод хорд и носит потому то же
название.
Предполагаем, как и в предыдущем разделе, что знаки
производной унимодальной функции ![]() на концах отрезка
на концах отрезка ![]() различны:
различны: ![]() ;
; ![]() .
.
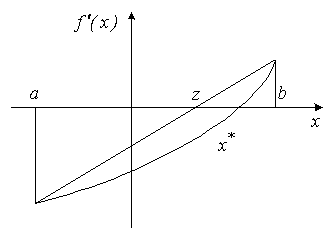
Тогда приближение ![]() к
стационарной точке
к
стационарной точке ![]() определится по формуле
определится по формуле
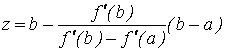 . (7.1.1)
. (7.1.1)
Алгоритм метода хорд тот же, что и алгоритм метода
средней точки за исключением того, что координата точки ![]() вычисляется
по формуле (7.1.1).
вычисляется
по формуле (7.1.1).
В качестве примера рассмотрим две итерации вычисления
координаты точки максимума функции ![]() на отрезке
на отрезке ![]() .
.
![]() .
.
Итерация 1.
![]() ;
; ![]() ;
;
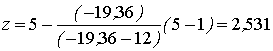 ;
;
![]() ;
; ![]() .
.
Итерация 2.
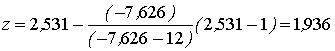 ;
;
![]() ;
; ![]() .
.
7.1.8. Метод кубической аппроксимации
В соответствии с этим
методом предполагается, что функция ![]() , которая подлежит
максимизации, хорошо аппроксимируется на отрезке
, которая подлежит
максимизации, хорошо аппроксимируется на отрезке ![]() полиномом
третьей степени. Построим этот полином по заданным значениям функции
полиномом
третьей степени. Построим этот полином по заданным значениям функции ![]() и
и ![]() и ее
производной
и ее
производной ![]() и
и ![]() (полином
Эрмита) в виде
(полином
Эрмита) в виде
![]() .
.
Коэффициенты ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
определяемые из условий
,
определяемые из условий ![]() ;
; ![]() ;
; ![]() ;
; ![]() , равны:
, равны:
![]() ;
; ![]() ;
;
![]() ;
; 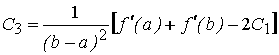 .
.
Точку максимума ![]() оценим точкой интерполяционного
полинома, для чего приравняем производную полинома нулю:
оценим точкой интерполяционного
полинома, для чего приравняем производную полинома нулю:
![]() .
.
Решая это квадратное уравнение, получим
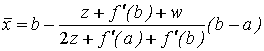 , (7.1.2)
, (7.1.2)
где
![]() ; (7.1.3)
; (7.1.3)
![]() . (7.1.4)
. (7.1.4)
Алгоритм метода кубической аппроксимации
Исходные данные. ![]() -
отрезок, содержащий точку максимума
-
отрезок, содержащий точку максимума ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() -
параметры окончания счета.
-
параметры окончания счета.
Если ![]() , то
, то ![]() ,
конец.
,
конец.
Вычислить ![]() по формулам (1.2)-(1.4).
по формулам (1.2)-(1.4).
Вычислить ![]() ;
; ![]() .
.
Если ![]() , то
, то ![]() ,
конец.
,
конец.
Если ![]() , то
, то ![]() ,
, ![]() ,
, ![]() ;
перейти к шагу 1.
;
перейти к шагу 1.
![]() ;
;
![]() ;
; ![]() ;
перейти к шагу 1.
;
перейти к шагу 1.
Пример 1.6. Найти точку
максимума функции ![]() на отрезке
на отрезке ![]() ;
; ![]() ;
; ![]() .
.
![]() .
.
Итерация 1.
![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
; ![]() .
.
Так как ![]() , продолжаем расчет.
, продолжаем расчет.
![]() ,
следовательно,
,
следовательно, ![]() .
.
Итерация 2.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
; ![]() .
.
Так как![]() , следовательно,
, следовательно, ![]() .
.
7.1.9. Метод Ньютона-Рафсона
Предполагаем, что
унимодальная функция ![]() дважды непрерывно
дифференцируема. Тогда для решения уравнения
дважды непрерывно
дифференцируема. Тогда для решения уравнения ![]() можно
применить метод касательных (Ньютона)
можно
применить метод касательных (Ньютона)
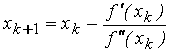 ,
, ![]() (7.1.5)
(7.1.5)
Алгоритм метода Ньютона-Рафсона
Исходные данные. ![]() -начальная
оценка координаты стационарной точки,
-начальная
оценка координаты стационарной точки, ![]() , -
параметр окончания счета.
, -
параметр окончания счета.
![]() .
.
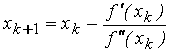 .
.
Если ![]() , то
, то ![]() ,
конец.
,
конец.
![]() ,
перейти к шагу 2.
,
перейти к шагу 2.
Пример 1.7. Найти точку
максимума функции ![]() на отрезке
на отрезке ![]() ,
, ![]() ,
, ![]() .
.
Итерация 1.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Итерация 2.
![]() ;
;
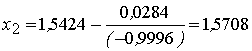 ;
;
![]() ,
, ![]() .
.
Последовательность (1.5) сходится к стационарной точке лишь при выполнении определенных условий, накладываемых на вид функции и выбор начальной точки (теорема о сходимости метода касательных).
Домашнее задание №20
Методом Свенна найти отрезок, содержащий точку экстремума
унимодальной функции ![]() . Вычислить точку экстремума:
. Вычислить точку экстремума:
I.
методом
золотого сечения, ![]() ;
;
II. методом средней точки
III. методом хорд;
IV. методом Ньютона-Рафсона
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()