§ 4

8. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Динамическое программирование есть особый метод оптимизации решений, специально приспособленный к так называемым «многошаговым», или «многоэтапным» операциям.

8.1. ПОСТАНОВКА ЗАДАЧИ

Представим себе некоторую операцию , распадающуюся на ряд последовательных шагов, - например, деятельность предприятия в течении нескольких хозяйственных лет; поэтапное планирование инвестиций; управление производственными мощностями в течение длительного срока; или же преодоление группой самолетов нескольких полос противовоздушной обороны; или же распределения весов многоступенчатой ракеты между ее ступенями с целью оптимизации скорости. Некоторые операции расчленяются на шаги естественно; в некоторых членение приходится вводить искусственно – скажем, процесс наведения ракеты на цель можно условно разбить на этапы, каждый из которых занимает какое-то время .

Рассмотрим управляемый процесс. Предположим, что управление можно разбить на шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему из начального состояния в конечное, представляет собой совокупность пошаговых управлений. В результате управления система переходит из состояния в .

Обозначим через управление на ом шаге (8.к = 1, 2, ..., n). – множество допустимых управлений на ом шаге.

Пусть – управление, переводящее систему из состояние в состояние . Обозначим через состояние системы после ого шага управления. Получаем последовательность состояний . (рисунок 8.1).

Рис. 8.1 Переход системы из одного состояния в другое в результате управляющих сигналов

Показатель эффективности рассматриваемой управляемой операции зависит от начального состояния и управления:

(8.1)

- множество возможных управлений

Сделаем несколько предположений:

1. Состояние системы на ом шаге зависит только от предшествующего состояния и управления на ом шаге и не зависит от предшествующих состояний и управлений (8.свойство отсутствия последействия):

уравнения состояний (8.2)

- оператор перехода

2. Целевая функция (8.1) является аддитивной от показателя эффективности каждого шага, т.е. выигрыш за всю операцию складывается из выигрышей на отдельных шагах.

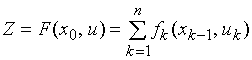(8.3)

показатель эффективности шага (8.4)

Общая постановка задачи ДП. Определить такое допустимое управление , переводящее систему из состояния в состояние , при котором целевая функция (8.3) принимает максимальное значение.

8.2. ПРИНЦИП РЕШЕНИЯ ЗАДАЧ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Любую многошаговую задачу можно решать по разному: либо искать сразу все элементы решения на всех шагах, либо же строить оптимальное управление шаг за шагом, на каждом этапе расчета оптимизируя лишь один шаг. Обычно второй способ оказывается проще, чем первый, особенно при большом числе шагов.

Такая идея постепенной, пошаговой оптимизации и лежит в основе метода динамического программирования. Оптимизация одного шага, как правило, проще оптимизации всего процесса: лучше, оказывается, много раз решить сравнительно простую задачу, чем один раз – сложную.

С первого взгляда идея может показаться довольно тривиальной. В самом деле, чего казалось бы проще: если трудно оптимизировать операцию в целом, разбить ее на ряд шагов. Каждый шаг будет отдельной, маленькой операцией, оптимизировать которую уже не трудно. Надо выбрать на этом шаге такое управление, чтобы эффективность этого шага была максимальна. Не так ли?

Нет! Принцип динамического программирования отнюдь не предполагает, что каждый шаг оптимизируется отдельно, независимо от других. Напротив, шаговое управление должно выбираться дальновидно, с учетом всех его последствий в будущем. Что толку, если мы выберем на данном шаге управление, при котором эффективность этого шага максимальна, если этот шаг лишит нас возможности хорошо выиграть на последующих шагах?

Пусть, например, планируется работа группы промышленных предприятий, из которых часть занята выпуском предметов потребления, а остальные производят для них машины. Задача операции – получить за лет максимальный объем выпуска предметов потребления. Допустим, планируются капиталовложения на первый год. Исходя из узких интересов этого шага, мы должны были бы все наличные средства вложить в производство предметов потребления. Но правильно ли будет такое решение с точки зрения эффективности операции в целом? Очевидно, нет. Это решение – недальновидное. Имея в виду будущее, надо выделить какую-то часть средств и на производство машин. От этого объем продукции за первый год, конечно, снизится, зато будут созданы условия для его увеличения в последующие годы.

Планируя многошаговую операцию, надо выбирать управление на каждом шаге с учетом всех его будущих последствий на еще предстоящих шагах. Управление на ом шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимален, а так, чтобы была максимальна сумма выигрышей на всех оставшихся до конца шагах плюс данный.

Принцип динамического программирования не предполагает, что каждый шаг оптимизируется отдельно, независимо от других. Напротив, шаговое управление должно выбираться дальновидно, с учетом всех его последствий в будущем.

Однако из этого правила есть исключение. Среди всех шагов есть один, который может планироваться попросту, без оглядки на будущее. Какой это шаг? Очевидно, последний! Этот шаг, единственный из всех, можно планировать так, чтобы он сам, как таковой, принес наибольшую выгоду.

Поэтому процесс динамического программирования обычно разворачивается от конца к началу: прежде всего планируется последний, ый шаг. А как его спланировать если мы не знаем, чем закончился предпоследний?

Планируя последний шаг, нужно сделать разные предположения о том, чем кончился предпоследний, -ый шаг, и для каждого из этих предположений найти условное оптимальное управление на м шаге. "Условное" потому, что оно выбирается исходя из условия, что предпоследний шаг кончился определенным образом.

Предположим, что мы это сделали, и для каждого их возможных исходов предпоследнего шага знаем условное оптимальное управление и соответствующий ему условный оптимальный выигрыш на м шаге. Теперь мы можем оптимизировать управление на предпоследнем, -шаге. Снова сделаем все возможные предположения о том, чем кончился предыдущий, -ой шаг, и для каждого из этих предположений найдем такое управление на -шаге, при котором выигрыш за последние два шага максимален. Так мы найдем для каждого исхода -го шага условное оптимальное управление на -м шаге и условный оптимальный выигрыш на двух последних шагах. Далее, «пятясь» назад, оптимизируем управление на -м шаге и т.д., пока не дойдем да первого.

Предположим, что все условные оптимальные управления и условные оптимальные выигрыши за весь «хвост» процесса нам известны. Это значит: мы знаем, что надо делать, как управлять на данном шаге и что мы за это получим на «хвосте», в каком бы состоянии ни был процесс к началу шага. Теперь мы можем построить уже не условно оптимальное, а просто оптимальное управление и найти не условно оптимальный, а просто оптимальный выигрыш .

В самом деле, пусть мы знаем, в каком состоянии была управляемая система в начале первого шага. Тогда мы можем выбрать оптимальное управление на первом шаге. Применив его, мы изменим состояние системы на некоторое новое ; в этом состоянии мы подошли ко второму шагу. Тогда нам тоже известно уловное оптимальное управление , которое к концу второго шага переводит систему в состояние , и т.д. Что касается оптимального выигрыша за всю операцию, то он нам уже известен: ведь именно на основе его максимальности мы выбирали управление на первом шаге.

Таким образом, в процессе оптимизации управления методом динамического программирования многошаговый процесс «проходится» дважды: первый раз – от конца к началу, в результате чего находятся условные оптимальные управления и условные оптимальные выигрыши за оставшийся «хвост» процесса; второй раз – от начала к концу, когда нам остается только «прочитать» уже готовое управления , состоящее из оптимальных шаговых управлений .

Первый этап - условная оптимизации - несравненно сложнее второго. Второй этап почти не требует дополнительных вычислений.

8.3. ПРИНЦИП ОПТИМАЛЬНОСТИ БЕЛЛМАНА. УРАВНЕНИЯ БЕЛЛМАНА

Предположим, что задача

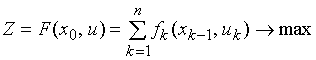
имеет решение.

Тогда справедлив принцип оптимальности Беллмана: оптимальное управление обладает тем свойством, что каковы бы ни были состояния системы на любом шаге и управление , принимаемое в этом состоянии, последующие управляющие решения , ..., должны составлять оптимальную стратегию относительно состояния , полученного в результате управляющего решения , т.е. состояния, к которому придет система в конце данного шага.

Другими словами: управление на каждом шаге необходимо выбирать так, чтобы оптимальной была сумма выигрышей на всех оставшихся до конца процесса шагах, включая выигрыш на данном шаге.

На основании принципа оптимальности Беллмана можно получить основное уравнение динамического программирования, или уравнение Беллмана.

Рассмотрим последовательность задач используя принцип оптимальности. На каждом шаге любого состояния системы управление нужно выбирать «с оглядкой», т.к. этот выбор влияет на последующее состояние и дальнейший процесс управления, зависящий от . Это следует из принципа оптимальности.

Как отмечалось ранее, среди всех шагов есть одно исключение, он может планироваться попросту, без оглядки на будущее – это последний шаг. Этот шаг единственный, который можно планировать так, чтобы он сам, как таковой, принес наибольшую выгоду.

Рассмотрим ый шаг: – состояние системы к началу го шага, – конечное состояние, – управление на шаге , а - целевая функция шага .

Согласно принципу оптимальности, нужно выбирать так, чтобы для любых состояний получить максимум целевой функции на этом шаге.

Обозначим через максимум показателя эффективности шага при условии, что к началу последнего шага система была в произвольном состоянии , а на последнем шаге управление было оптимальным.

(8.5)

Управление , при котором достигается максимум (8.5) также зависит от и называется условным оптимальным управлением шага и обозначается .

Решив задачу (8.5), найдем для всех возможных состояний две функции: и .

Рассмотрим двухшаговую задачу: присоединим к му шагу -ый (рисунок 8.2).

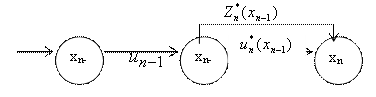
Рис. 8.2. Оптимальное управление на двух последних шагах

Для любых состояний , произвольных управлений и оптимального управления на шаге значение целевой функции на двух последних шагах равно:

(8.6)

Согласно принципу оптимальности для любых состояний управление нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем шаге приводило бы к максимальному эффекту на двух последних шагах. Следовательно, необходимо искать максимум (8.6) по всем допустимым .

(8.7)

В результате максимизации получаем две функции: и .

Далее рассматривается трехшаговая задача: к двум последним добавляется -ой и т.д.

Обозначим через условный максимум целевой функции, полученный при оптимальном управлении на шагах, начиная с го до конца, при условии, что к началу го шага система находится в состоянии .

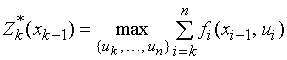
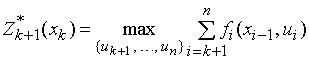
Целевая функция на последних шагах при произвольном управлении на ом шаге и оптимальном управлении на последующих шагах равна .

Согласно принципу оптимальности, выбирается из условия максимума этой суммы, т.е.

(8.8)

Уравнения (8.8) называются уравнениями Беллмана. Это рекуррентные соотношения, позволяющие найти предыдущие значения функции, зная последующие. Процесс решения уравнений (8.5) и (8.8) называется условной оптимизацией.

В результате условной оптимизации получаем две последовательности: и .

Используя эти последовательности, можно найти решение задачи динамического программирования при данных и : .

Домашнее задание №23

Задание 1. Найти оптимальное распределение средств между тремя предприятиями при условии, что прибыль , полученная от ого предприятия, является функцией от вложенных в него средств . Функции заданы таблично:

1	2	3	4	5	6	7	8
5	6	7	9	9	11	12	14
0	3	4	6	7	9	12	13
4	4	6	6	8	8	10	10

1	2	3	4	5	6	7	8
2	6	8	9	9	11	12	14
2	4	6	8	8	9	12	13
4	4	6	6	8	8	10	10

1	2	3	4	5	6	7	8
5	6	7	7	9	10	12	14
2	3	4	6	7	9	12	13
3	4	6	7	8	9	10	10

1	2	3	4	5	6	7	8
0	6	7	9	9	11	12	14
2	3	5	7	9	9	12	13
4	4	6	6	8	9	10	12

1	2	3	4	5	6	7	8
3	4	6	9	9	11	12	14
4	4	5	6	7	9	12	13
4	4	6	6	8	8	10	10

2	4	6	8	10	12	14	16
5	6	8	12	12	15	16	17
0	5	7	9	12	14	16	18
4	7	7	10	11	13	16	17

2	4	6	8	10	12	14	16
3	6	8	11	12	15	16	17
4	6	8	11	12	14	16	18
4	7	7	10	11	13	16	17

2	4	6	8	10	12	14	16
3	6	7	10	12	14	15	17
3	6	7	9	12	14	16	18
4	7	7	10	11	13	16	17

2	4	6	8	10	12	14	16
5	6	8	12	12	15	16	17
4	5	7	9	11	14	16	18
0	7	7	10	12	15	17	19

10.

2	4	6	8	10	12	14	16
5	6	8	12	12	15	16	17
4	5	8	11	13	15	15	18
4	7	8	10	11	13	16	18

Задание 2. Найти оптимальное распределение ресурсов между двумя отраслями производства в течение четырех лет, если даны функции доходов и для каждой отрасли и функции возврата и . По истечении года все возвращенные средства перераспределяются, доход в производство не вкладывается.