Логические операции и базовые элементы компьютера

 

В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые высказывания. Истинность полученных высказываний зависит от истинности исходных высказываний и использованных для их преобразования логических операций.

Для образования новых высказываний наиболее часто используются логические операции, выражаемые словами «не», «и», «или».

Логический элемент компьютера— это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию.

Логическими элементами компьютеров являются электронные схемы «И», «ИЛИ», «НЕ», «И—НЕ», «ИЛИ—НЕ» и другие (называемые также вентилями), а также триггер.

Можно доказать, что с помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.

Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.

Высокий уровень обычно соответствует значению “истина”(true)- “1”, а низкий — значению “ложь” (false) - “0”.

Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Работу логических элементов описывают с помощью таблиц истинности.

Рассмотрим логические операции и соответствующие им элементы логических схем.

Конъюнкция. Соединение двух (или нескольких) высказываний в одно с помощью союза И (OR) называется операцией, логического умножения, или конъюнкцией. Эту операцию принято обозначать знаками «Ù, &» или знаком умножения «´». Сложное высказывание А&В истинно только в том случае, когда истинны оба входящих в него высказывания. Истинность такого высказывания задается следующей таблицей:

 

 

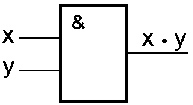
Логическая схема «И»реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы «И» с двумя входами представлено на рис.7 а.

Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.

Связь между выходом  z  этой схемы и входами  x  и  y  описывается соотношением:   z = x .& y (читается как "x и y"). Операция конъюнкции на структурных схемах обозначается знаком  "&"

Дизъюнкция. Объединение двух (или нескольких) высказываний с помощью союза ИЛИ (OR) называется операцией логического сложения, или дизъюнкцией. Эту операцию обозначают знаками «½,Ú» или знаком сложения «+». Сложное высказывание AÚB истинно, если истинно хотя бы одно из входящих в него высказываний. Таблица истинности для логической суммы высказываний имеет вид:

 

 

В последнем столбце данной таблицы размещены результаты модифицированной операции ИЛИ - ИСКЛЮЧАЮЩЕЕ ИЛИ  (XOR). Отличающееся от обычного ИЛИ последней строкой (см. также рис.7 в, г).

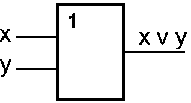
Схема «ИЛИ» реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы «ИЛИ» будет единица, на её выходе также будет единица.

 

а).	б)
в)	г)
д)	е)

 

Рис. 7. Схемные логические элементы вычислительных машин

 

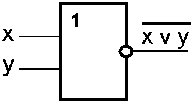
Условное обозначение на структурных схемах схемы «ИЛИ» с двумя входами представлено на рис. 7 б)  Знак "1" на схеме — от классического обозначения дизъюнкции как  >=1  (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом  z  этой схемы и входами  x  и  y   описывается соотношением:  z = x V y  (читается как "x или y").

Инверсия. Присоединение частицы  НЕ (NOT) к данному высказыванию называется операцией отрицания (инверсии). Она обозначается Ā (или А)и читается не А . Если высказывание А истинно, то В ложно, и наоборот. Таблица истинности в этом случае имеет вид:

 

 

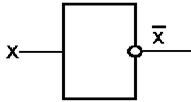
Схема «НЕ» (инвертор) реализует операцию отрицания.  Связь между входом   x этой схемы и выходом  z  можно записать соотношением   z =, где читается как "не x" или "инверсия х".

Если на входе схемы  0,  то на выходе  1.  Когда на входе  1,  на выходе  0.  Условное обозначение на структурных схемах инвертора — на рис. 7 в).

Кроме схемных элементов, соответствующих перечисленным логическим операторам, в состав логических схем входят комбинированные связки, именуемые вентилями, а именно:

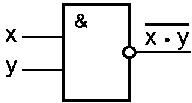
Схема «И—НЕ» состоит из элемента «И» и инвертора и осуществляет отрицание результата схемы «И». Связь между выходом z и входами x и y схемы записывают следующим образом: , или "инверсия x и y".  Условное обозначение на структурных схемах схемы  «И—НЕ» с двумя входами представлено на рис. 7 г

 

Таблица истинности схемы «И—НЕ»

 

Схема «ИЛИ—НЕ» состоит из элемента «ИЛИ» и инвертора и осуществляет отрицание результата схемы «ИЛИ».  Связь между выходом z и входами  x  и  y  схемы записывают следующим образом: , т.е. "инверсия  x или y ". Условное обозначение на структурных схемах схемы «ИЛИ—НЕ» с двумя входами представлено на рис. 7 д.

 

Таблица истинности схемы «ИЛИ—НЕ»

 

Схема «ИСКЛЮЧАЮЩЕЕ ИЛИ» (рис. 9 е)  соответствует «сложению по модулю 2). См. также таблицу истинности для дизъюнкции.

Помимо операций И, ИЛИ, НЕ в алгебре высказываний существует ряд других операций. Например, операция эквиваленции (эквивалентности) А~В ( или АºВ, A eqv B), которая имеет следующую таблицу истинности:

 

А	В	А~В
false	false	true
false	true	false
true	false	false
true	true	true

 

Другим примером может служить логическая операция импликации или логического следования (А®В, A imp B), объединяющая высказывания словами «если..., то» и имеющая следующую таблицу истинности:

 

 

Высказывания, образованные с помощью логических операций, называются сложными. Истинность сложных высказываний можно установить, используя таблицы истинности. Например, истинность сложного высказывания Ā&В определяется следующей таблицей:

 

А	В	Ā	В	Ā&В
false	false	true	true	true
false	true	true	false	false
true	false	false	true	false
true	true	false	false	false

 

Высказывания, у которых таблицы истинности совпадают, называются равносильными. Для обозначения равносильных высказываний используют знак «=» (A = B). Рассмотрим сложное высказывание (А&В)|(В &) и запишем таблицу истинности этого высказывания:

 

А	В	В		А&В	В&	(В&)|(А&В)
false	false	true	true	false	true	true
false	true	true	false	false	false	false
true	false	false	true	false	false	false
true	true	false	false	true	false	true

 

Если сравнить эту таблицу с таблицей истинности операции эквивалентности высказываний А и В, то можно увидеть, что высказывания (А&В)|(В &) и А~В тождественны, т.е. А~В = (А&В)|(В &).

В алгебре высказываний можно проводить тождественные преобразования, заменяя одни высказывания равносильными им другими высказываниями.

Исходя из определений дизъюнкции, конъюнкции и отрицания, устанавливаются свойства этих операций и взаимные распределительные свойства. Приведем примеры некоторых из этих свойств:

Коммутативность (перестановочность)

 

Закон идемпотентности

А&А = А, AÚA=A,

Двойное отрицание

Сочетательные (ассоциативные) законы

Распределительные (дистрибутивные) законы

Поглощение

Склеивание

Операция переменной с ее инверсией

Операция с константами

Законы де Моргана

1.  (условно его можно назвать 1-й);

2.  (2-й)- описывают результаты отрицания переменных, связанных операциями  И, ИЛИ.

 

В следующей таблице приведено доказательство истинности дистрибутивного закона.

 

 

Аналогичным образом могут быть доказаны и другие тождества.

Высказывания, образованные при помощи нескольких операций логического сложения, умножения и отрицания   называются сложными. Истинность всякого сложного высказывания устанавливается с помощью таблиц истинности. Высказывания , у которых таблицы истинности совпадают называются равносильными высказываниями. Сложные высказывания истины для любых значений истинности, входящих в них простых  высказываний, называются тождественно истинными. Тождественно ложными называются формулы, принимающие значение (false) для любых значений истинности, входящих в него простых высказываний.

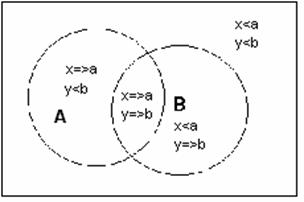
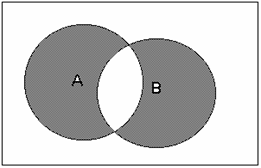
На рис. 8 а - ж приведены иллюстрации к основным логическим операциям и их композициям (т.н. диаграммы Эйлера-Венна). В качестве высказывания А здесь принято утверждение x=>a, в качестве В - y=>b. На рис. 8.а приведены области истинности каждого из высказываний, здесь же становится понятен смысл дополнения (отрицания), объединения (дизъюнкции), пересечения (конъюнкции) и др. операций.

Первый из законов де Моргана иллюстрируется рис. 8 д, ж.

Логическое значение NULL.В некоторых ЯП (Visual Basic  и пр.) для расширения применимости логических выражений на те случаи, когда значение одного или нескольких логических аргументов неизвестны или не определены, вводится значение null (в дополнение к false и true), как правило, такое значение присваивается компилятором логической переменной по умолчанию.

 

 

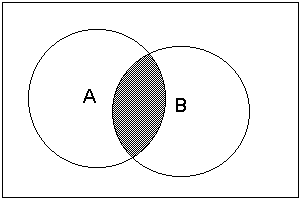
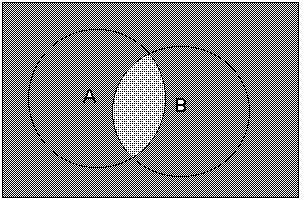
а). Диаграмма Эйлера-Венна, иллюстрирующая расположение областей истинности высказываний А и В	б). Конъюнкция высказываний А и В (AND)
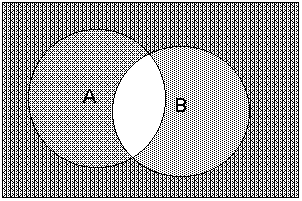
в). Дизъюнкция высказываний А и В (OR)/	г). Исключающая дизъюнкция (XOR).
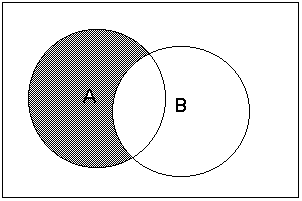
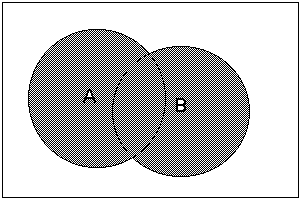
д). Разность высказываний (А - В)	е). Иллюстрация к законам де Моргана (дополнение пересечению высказываний)
ж). Иллюстрация к законам де Моргана (пересечение дополнений)   Рис. 8. Некоторые примеры диаграмм Эйлера-Венна

 

С учетом значения null таблицы истинности основных логических операций приобретают следующий вид.

 

Таблица 6

Операция отрицания (одноместная, унарная)

 

 

Таблица 7

Некоторые двуместные (бинарные) операции

 

 

Побитовые операции.В некоторых современных ЯП включены операции побитового сравнения содержимого машинных слов (которые могут содержать числовые, строчные и др. данные) при этом каждый бит результата образуется в соответствии с Табл. 7 (для бинарных операций). Унарная операция отрицания (not) в данном случае реализует очевидную замену 1 на 0 и наоборот.

 

Таблица 8

Операнды и результаты некоторых операций побитового сравнения

 

 

Другие схемные элементы ЭВМ

 

Регистр или триггер — это электронная схема, широко применяемая в регистрах компьютера для запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю.

Термин триггер происходит от английского слова trigger — защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает "хлопанье". Это звукоподражательное название электронной схемы указывает на её способность мгновенно переходить ("перебрасываться") из одного состояния в другое и обратно.

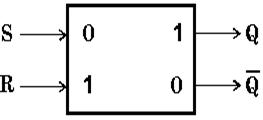
Самый распространённый тип триггера — так называемый RS-триггер (S и R, соответственно, от английских set — установка, и reset — сброс). Условное обозначение триггера — на рис. 9 а.

 

 

Рис. 9. Схемный элемент RS-триггер

 

Он имеет два симметричных входа S и R и два симметричных выхода Q и, причем выходной сигнал Q является логическим отрицанием сигнала .

На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов ().

Наличие импульса на входе считается единицей, а его отсутствие — нулем.

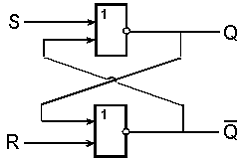
На рис. 9 б показана реализация триггера с помощью вентилей «ИЛИ—НЕ» и соответствующая таблица истинности.

 

Таблица 9

 

 

Перечислим возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы «ИЛИ—НЕ» (табл. 9).

1. Если на входы триггера подать S="1", R="0", то (независимо от состояния) на выходе Q верхнего вентиля появится "0". После этого на входах нижнего вентиля окажется R="0", Q="0" и выход станет равным "1".

2. При подаче "0" на вход S и "1" на вход R на выходе  появится "0", а на Q= "1".

3. Если на входы R и S подана логическая "1", то состояние Q и  не меняется.

4. Подача на оба входа R и S логического "0" может привести к неоднозначному результату, поэтому эта комбинация входных сигналов запрещена.

Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 ´210 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.

Полусумматор. Вспомним, что при сложении двоичных чисел образуется сумма в данном разряде, при этом возможен перенос в старший разряд. Обозначим слагаемые (А, В), перенос (P) и сумму (S). Таблица сложения одноразрядных двоичных чисел с учетом переноса в старший разряд выглядит следующим образом,

 

 

Из этой таблицы сразу видно, что перенос может реализовать с помощью операции логического умножения,

P=A&B.

Получим теперь формулу для вычисления суммы. Значения суммы более всего совпадают с результатом операции логического сложения (кроме случая, когда на вход подаются две единицы, а на выходе должен получится нуль).

 

 

 

 

 

 

 

 

 

 

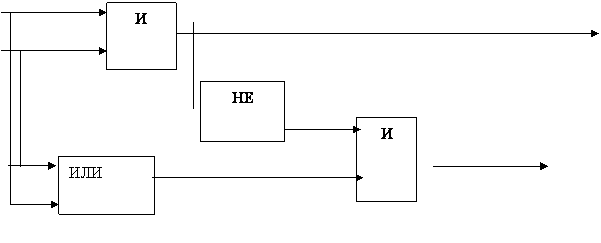
          А(0,0,1,1)                                                      P(0,0,0,1)

          В(0,1,0,1)

 

 

 

                                0,0,0,1                                 1,1,1,0

 

                                                                                                              S(0110)

 

 

 

 

Рис. 10. Логическая схема полусумматора

 

Нужный результат достигается, если результат логического сложения умножить на инвертированный перенос. Таким образом, для определения суммы можно применить выражение:

Теперь, на основе полученных логических выражений, можно построить из базовых логических элементов схему полусумматора.

По логической формуле переноса легко определить, что для получения переноса необходимо использовать логический элемент «И».

Из логической формулы для суммы очевидно, что на выходе должен стоять элемент логического умножения «И», который имеет два входа. На один из входов подается результат логического сложения исходных величин, т.е. на него должен подаваться сигнал с элемента логического сложения «ИЛИ».

На второй вход требуется подать результат инвертированного логического умножения исходных сигналов

То есть на второй вход подается сигнал с элемента «НЕ», на вход которого получает сигнал с элемента логического умножения «И».

Данная схема, называется полусумматором, так как реализует суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.

Полный одноразрядный сумматор. Полный одноразрядный сумматор должен иметь три входа, ai, bi - слагаемые и pi-1 - перенос из предыдущего разряда и два выхода, сумма ci  и перенос pi. Таблица сложения в этом случае будет иметь следующий вид,

 

 

 

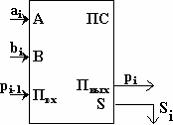
Рис. 11. Укрупненная схема одноразрядного сумматора

 

Идея построена полного сумматора точно такая же, как и полусумматора. Перенос реализуется с помощью формулы для его  получения

Логическое выражение для вычисления суммы в полном сумматоре принимает  следующий вид,

Укрупненная схема, соответствующая полному сумматору приведена на рис. 11. Составить соответствующую схему из вентилей мы рекомендуем читателю самостоятельно.

Более сложные комбинации логических элементов (узлы) рассмотрены ниже.

 

 

К оглавлению

Назад к разделу "Элементы матлогики или логические основы алгоритмизации. Логические элементы вычислительных машин"

Вперед к разделу "Преобразования логических формул"